DeepMind wies darauf hin, dass „Transformer nicht über die Daten vor dem Training hinaus verallgemeinern kann“, aber einige Leute stellten dies in Frage.

Ist Transformer dazu bestimmt, nicht in der Lage zu sein, neue Probleme zu lösen, die über „Trainingsdaten“ hinausgehen?

Apropos beeindruckende Fähigkeiten großer Sprachmodelle: Eine davon ist die Fähigkeit, Lernen in wenigen Schritten zu erreichen, indem Beispiele im Kontext bereitgestellt und das Modell aufgefordert werden, eine Antwort basierend auf der endgültigen bereitgestellten Eingabe zu generieren. Dies basiert auf der zugrunde liegenden maschinellen Lerntechnologie „Transformer-Modell“ und sie können auch kontextbezogene Lernaufgaben in anderen Bereichen als der Sprache durchführen.

Basierend auf früheren Erfahrungen wurde nachgewiesen, dass für Aufgabenfamilien oder Funktionsklassen, die in der vorab trainierten Mischung gut vertreten sind, die Auswahl geeigneter Funktionsklassen für kontextuelles Lernen nahezu kostenlos ist. Daher glauben einige Forscher, dass Transformer sich gut auf Aufgaben oder Funktionen verallgemeinern lässt, die mit der gleichen Verteilung wie die Trainingsdaten verteilt sind. Eine häufige, aber ungelöste Frage lautet jedoch: Wie funktionieren diese Modelle bei Stichproben, die nicht mit der Trainingsdatenverteilung übereinstimmen?

In einer aktuellen Studie sind Forscher von DeepMind dieser Frage mithilfe empirischer Forschung nachgegangen. Sie erklären das Generalisierungsproblem wie folgt: „Kann ein Modell gute Vorhersagen mit kontextbezogenen Beispielen generieren, indem es Funktionen verwendet, die zu keiner Basisfunktionsklasse in der Mischung vorab trainierter Daten gehören, und zwar aus einer Funktion, die keiner der Basisfunktionen angehört?“ Funktionsklassen, die in der Datenmischung vor dem Training zu sehen sind?)》

Der Schwerpunkt dieses Inhalts liegt auf der Untersuchung der Auswirkungen der im Vortrainingsprozess verwendeten Daten auf die Lernfähigkeit des resultierenden Transformer-Modells mit wenigen Schüssen. Um dieses Problem zu lösen, untersuchten die Forscher zunächst die Fähigkeit von Transformer, während des Vortrainingsprozesses verschiedene Funktionsfamilien für die Modellauswahl auszuwählen (Abschnitt 3) und beantworteten dann das OOD-Generalisierungsproblem mehrerer Schlüsselfälle (Abschnitt 4)

Link zum Papier: https://arxiv.org/pdf/2311.00871.pdf

Bei ihrer Forschung wurde Folgendes festgestellt: Erstens weist der vorab trainierte Transformer eine schlechte Leistung bei der Vorhersage von Funktionen auf, die aus der vorab trainierten Funktionsklasse extrahiert wurden. Bei konvexer Kombination ist dies sehr schwierig. Zweitens kann Transformer seltenere Teile des Funktionsklassenraums effektiv verallgemeinern. Wenn die Aufgabe jedoch ihren Verteilungsbereich überschreitet, kann Transformer nicht über die Datenerkennung vor dem Training hinaus verallgemeinern kann Probleme nicht lösen, die über die Erkenntnis hinausgehen

Im Allgemeinen sind die Beiträge dieses Artikels wie folgt:

Verwenden einer Mischung verschiedener Funktionsklassen zum Vorabtrainieren des Transformer-Modells, um Kontextlernen durchzuführen und zu beschreiben die Merkmale des Modellauswahlverhaltens;
Für Funktionen, die mit den Funktionsklassen in den vorab trainierten Daten „inkonsistent“ sind, wird das Verhalten des vorab trainierten Transformer-Modells beim Kontextlernen untersucht
Strong Strong Es wurde nachgewiesen, dass Modelle während des Kontextlernens mit geringem zusätzlichen statistischen Aufwand eine Modellauswahl unter vorab trainierten Funktionsklassen durchführen können. Es gibt jedoch auch nur begrenzte Beweise dafür, dass Modelle über ihren vorab trainierten Datenumfang hinaus Kontextlernverhalten ausführen können.
Dieser Forscher glaubt, dass dies eine gute Nachricht für die Sicherheit sein könnte, zumindest wird sich das Modell nicht so verhalten, wie es möchte

Aber einige Leute wiesen darauf hin, dass das in diesem Artikel verwendete Modell nicht für GPT geeignet ist -2 Skala“ bedeutet, dass das Modell in diesem Artikel etwa 1,5 Milliarden Parameter umfasst, was in der Tat schwer zu verallgemeinern ist.

Als nächstes werfen wir einen Blick auf die Details des Papiers.

Modellauswahlphänomen

Wenn Sie Datenmischungen verschiedener Funktionsklassen vorab trainieren, werden Sie auf ein Problem stoßen: Wenn das Modell auf Kontextbeispiele trifft, die von der Mischung vor dem Training unterstützt werden, wie wählt man zwischen verschiedenen Funktionsklassen aus? Treffen Sie eine Auswahl ?

In der Forschung wurde festgestellt, dass ein Modell, wenn es kontextbezogenen Stichproben im Zusammenhang mit Funktionsklassen in Pre-Training-Daten ausgesetzt wird, in der Lage ist, die besten (oder nahezu besten) Vorhersagen zu treffen. Die Forscher untersuchten auch die Leistung des Modells bei Funktionen, die keiner einzelnen Komponentenfunktionsklasse angehören, und diskutierten in Abschnitt 4

Funktionen, die überhaupt nichts mit den Daten vor dem Training zu tun haben

Zunächst beginnen wir mit der Untersuchung linearer Funktionen. Wir können sehen, dass lineare Funktionen im Bereich des kontextuellen Lernens große Aufmerksamkeit erregt haben. Letztes Jahr veröffentlichten Percy Liang und andere von der Stanford University einen Artikel mit dem Titel „What Can Transformers Learn in Context?“ Eine Fallstudie einer einfachen Funktionsklasse zeigte, dass der vorab trainierte Transformator beim Erlernen neuer linearer Funktionskontexte sehr gut abschnitt und fast das optimale Niveau erreichte

Sie betrachteten insbesondere zwei Modelle: eines in dichten linearen Funktionen (lineares A-Modell, auf dem trainiert wurde). eine dünn besetzte lineare Funktion (alle Koeffizienten des Modells sind ungleich Null) und das andere ist ein Modell, das auf einer dünn besetzten linearen Funktion trainiert wurde (nur 2 von 20 Koeffizienten sind ungleich Null). Die Leistung jedes Modells war vergleichbar mit der linearen Regression und der Lasso-Regression für die neue dichte lineare Funktion bzw. die dünn besetzte lineare Funktion. Darüber hinaus verglichen die Forscher diese beiden Modelle mit Modellen, die auf einer Mischung aus dünn besetzten linearen Funktionen und dichten linearen Funktionen vorab trainiert wurden.

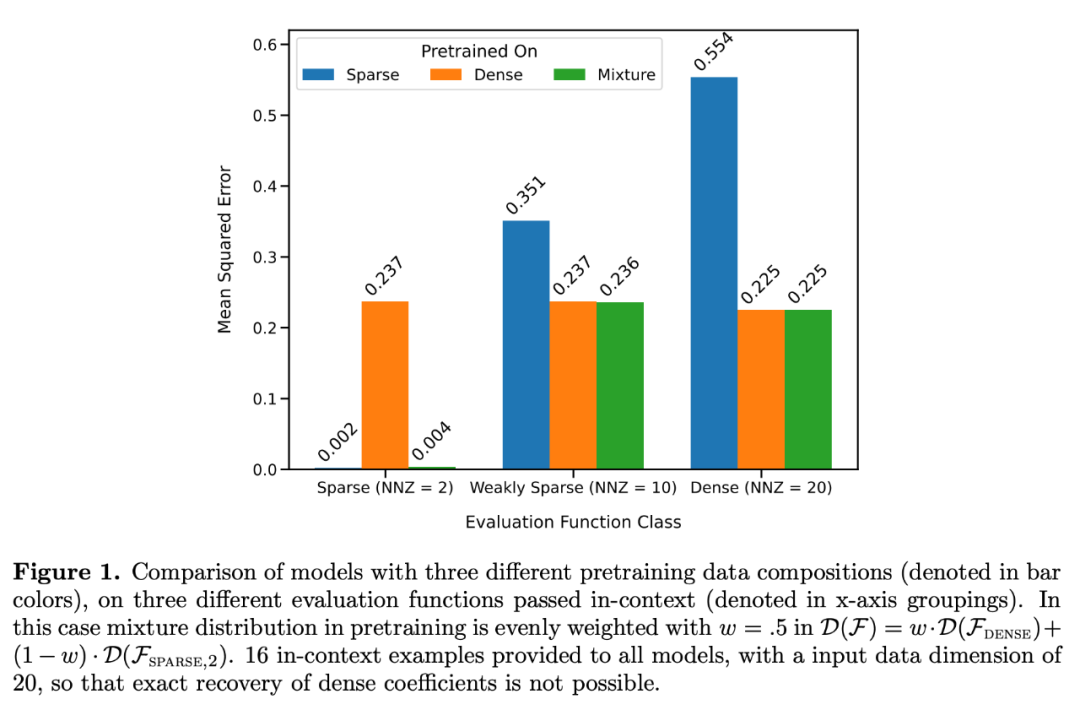
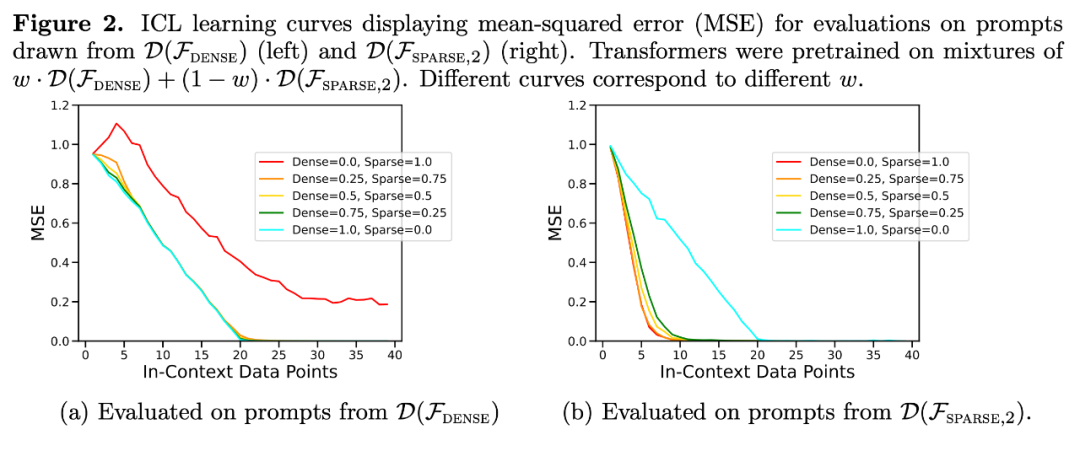
Wie in Abbildung 1 dargestellt, ähnelt die Leistung des Modells beim Kontextlernen auf einer 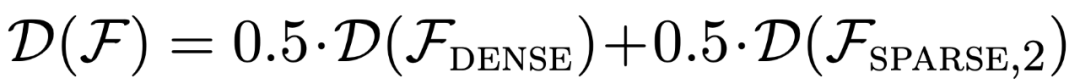Mischung einem Modell, das nur auf einer Funktionsklasse vorab trainiert wurde. Da die Leistung des vorab trainierten Hybridmodells dem theoretisch optimalen Modell von Garg et al. [4] ähnelt, schließen die Forscher, dass das Modell ebenfalls nahezu optimal ist. Die ICL-Lernkurve in Abbildung 2 zeigt, dass diese Fähigkeit zur Kontextmodellauswahl relativ mit der Anzahl der bereitgestellten Kontextbeispiele übereinstimmt. In Abbildung 2 ist auch zu erkennen, dass für bestimmte Funktionsklassen verschiedene nicht triviale Gewichte 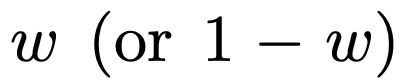verwendet werden.

Die ICL-Lernkurve entspricht nahezu der besten Basiskomplexität der Stichprobe. Die Abweichung ist gering und nimmt schnell ab, wenn die Anzahl der ICL-Stichproben zunimmt, was mit den Punkten auf der ICL-Lernkurve in Abbildung 1 übereinstimmt. Abbildung 2 zeigt, dass die ICL-Verallgemeinerung des Transformer-Modells durch Out-of-Distribution-Effekte beeinflusst wird. Obwohl sowohl die dichte lineare Klasse als auch die dünn besetzte lineare Klasse lineare Funktionen sind, können Sie sehen, dass die rote Kurve in Abbildung 2a (entsprechend dem Transformer, der nur für die dünn besetzte lineare Funktion vorab trainiert und anhand der dichten linearen Daten ausgewertet wurde) eine schlechte Leistung aufweist Umgekehrt ist die Leistung der braunen Kurve in Abbildung 2b ebenfalls schlecht. Forscher haben auch ein ähnliches Verhalten in anderen nichtlinearen Funktionsklassen beobachtet

Zurück zum Experiment in Abbildung 1, bei dem der Fehler als Funktion der Anzahl von Nicht-Null-Koeffizienten über den gesamten möglichen Bereich aufgetragen wird, zeigen die Ergebnisse, dass wenn w = . Das auf der Mischung von 5 vorkonditionierte Modell

funktioniert während des gesamten Prozesses genauso gut wie das auf der Mischung vorkonditionierte Modell (d. h. w = 0 und w = 1) (Abb. 3a). Dies zeigt, dass das Modell bei der Modellauswahl in der Lage ist, zu entscheiden, ob Vorhersagen nur anhand der Kenntnis einer Basisfunktionsklasse oder einer anderen Basisfunktionsklasse in der vorab trainierten Mischung getroffen werden sollen.

Tatsächlich zeigt Abbildung 3b, dass, wenn die im Kontext bereitgestellten Stichproben entweder aus sehr spärlichen oder sehr dichten Funktionen stammen, die Vorhersagen fast identisch mit denen eines Modells sind, das vorab trainiert wurde, indem nur spärliche Daten oder nur dichte Daten verwendet wurden. Dazwischen jedoch, wenn die Anzahl der Koeffizienten ungleich Null ≈ 4 ist, weichen die Hybridvorhersagen von denen des rein dichten oder rein spärlichen vortrainierten Transformers ab.

Dies zeigt, dass das auf der Mischung vorab trainierte Modell nicht einfach eine einzelne Funktionsklasse zur Vorhersage auswählt, sondern ein Ergebnis dazwischen vorhersagt.

Einschränkungen der Modellauswahlfähigkeit

Als nächstes untersuchten die Forscher die ICL-Generalisierungsfähigkeit des Modells aus zwei Perspektiven. Erstens wird die ICL-Leistung von Funktionen getestet, denen das Modell während des Trainings nicht ausgesetzt war. Zweitens wird die ICL-Leistung extremer Versionen von Funktionen bewertet, denen das Modell während des Trainings ausgesetzt war Es wurden kaum Hinweise auf eine Verallgemeinerung außerhalb der Verteilung gefunden. Wenn die Funktion stark von der Funktion vor dem Training abweicht, ist die Vorhersage instabil. Wenn die Funktion nahe genug an den Daten vor dem Training liegt, kann sich das Modell gut annähern

Die Vorhersagen von Transformer auf mittleren Sparsity-Ebenen (nnz = 3 bis 7) ähneln nicht den Vorhersagen einer Funktionsklasse, die durch das Vortraining bereitgestellt wird, sondern liegen irgendwo dazwischen, wie in Abbildung 3a dargestellt. Daraus können wir schließen, dass das Modell über eine Art induktive Tendenz verfügt, die es ihm ermöglicht, vorab trainierte Funktionsklassen auf nicht triviale Weise zu kombinieren. Wir können beispielsweise vermuten, dass das Modell Vorhersagen basierend auf der Kombination von Funktionen generieren kann, die während des Vortrainings beobachtet wurden. Um diese Hypothese zu testen, haben wir die Möglichkeit untersucht, ICL auf lineare Funktionen, Sinuskurven und konvexe Kombinationen der beiden anzuwenden. Sie konzentrieren sich auf den eindimensionalen Fall, um die Bewertung und Visualisierung der nichtlinearen Funktionsklasse zu erleichtern

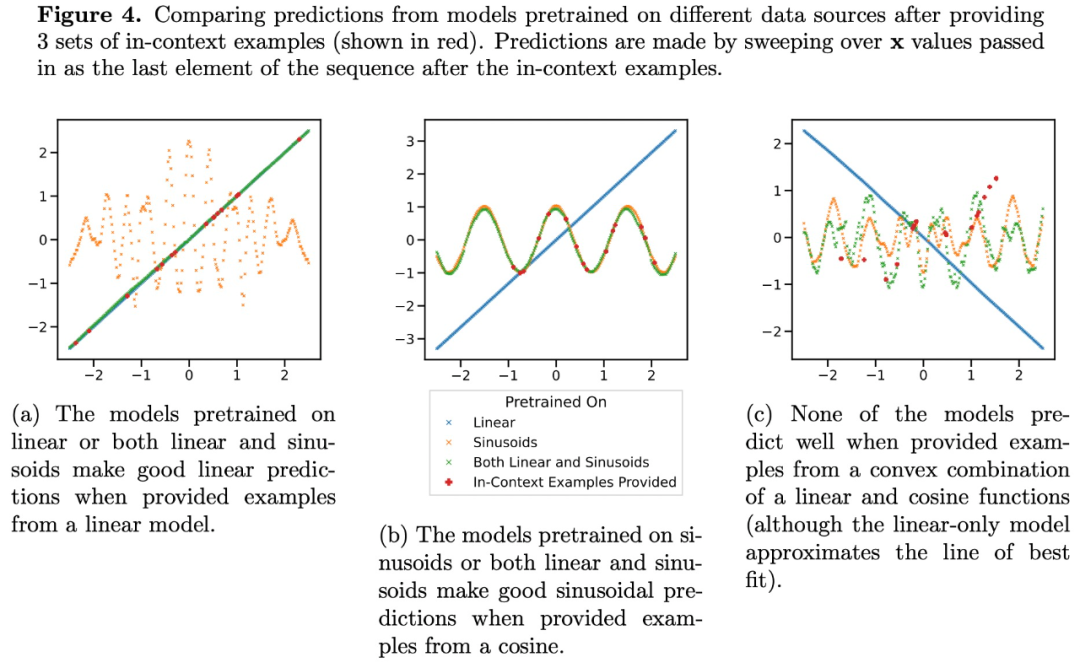
Abbildung 4 zeigt, dass das auf einer Mischung aus linearen Funktionen und Sinuskurven (d. h. ) vorab trainierte Modell zwar in der Lage ist, beide getrennt vorherzusagen. Entweder Wenn eine der Funktionen gute Vorhersagen macht, kann sie nicht zu einer konvexen Kombinationsfunktion beider passen. Dies deutet darauf hin, dass das in Abbildung 3b gezeigte Phänomen der linearen Funktionsinterpolation keine verallgemeinerbare induktive Tendenz des kontextuellen Lernens von Transformer ist. Es unterstützt jedoch weiterhin die engere Annahme, dass das Modell in der Lage ist, die beste Funktionsklasse für die Vorhersage auszuwählen, wenn die Kontextstichprobe nahe an der im Vortraining erlernten Funktionsklasse liegt.

Weitere Forschungsdetails finden Sie im Originalpapier

Das obige ist der detaillierte Inhalt vonDeepMind wies darauf hin, dass „Transformer nicht über die Daten vor dem Training hinaus verallgemeinern kann“, aber einige Leute stellten dies in Frage.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!