​Mit fast der Hälfte der Parameter liegt die Leistung nahe an Google Minerva, einem weiteren großen mathematischen Modell, das Open Source ist

Heutzutage zeigen Sprachmodelle, die auf verschiedenen textgemischten Daten trainiert wurden, sehr allgemeine Sprachverständnis- und Generierungsfähigkeiten und können als Basismodelle zur Anpassung an verschiedene Anwendungen verwendet werden. Anwendungen wie offener Dialog oder Befehlsverfolgung erfordern eine ausgewogene Leistung über die gesamte natürliche Textverteilung und bevorzugen daher Allzweckmodelle.

Wenn Sie jedoch die Leistung in einem bestimmten Bereich (z. B. Medizin, Finanzen oder Wissenschaft) maximieren möchten, bietet ein domänenspezifisches Sprachmodell möglicherweise bessere Funktionen bei einem bestimmten Rechenaufwand oder zu einem höheren Preis Der Rechenaufwand sorgt für ein bestimmtes Leistungsniveau.

Forscher der Princeton University, EleutherAI und anderen haben ein domänenspezifisches Sprachmodell trainiert, um mathematische Probleme zu lösen. Sie glauben, dass: Erstens erfordert die Lösung mathematischer Probleme einen Mustervergleich mit einem großen Maß an beruflichem Vorwissen, sodass es sich um ein ideales Umfeld für das Domänenanpassungstraining handelt, zweitens ist das mathematische Denken selbst die Kernaufgabe der KI; starkes mathematisches Denken Sprachmodelle sind vielen Forschungsthemen vorgelagert, wie z. B. Belohnungsmodellierung, Inferenzverstärkungslernen und algorithmisches Denken.

Daher schlagen sie eine Methode zur Anpassung von Sprachmodellen an die Mathematik durch kontinuierliches Vortraining von Proof-Pile-2 vor. Proof-Pile-2 ist eine Mischung aus mathematikbezogenem Text und Code. Die Anwendung dieses Ansatzes auf Code Llama führt zu LLEMMA: einem Basissprachenmodell für 7B und 34B mit deutlich verbesserten mathematischen Fähigkeiten.

Papieradresse: https://arxiv.org/pdf/2310.10631.pdf

Projektadresse: https://github.com/EleutherAI/math-lm

LLEMMA Die 4-Schuss-Matheleistung von 7B übertrifft die von Google Minerva 8B bei weitem, und die Leistung von LLEMMA 34B kommt der von Minerva 62B mit fast der Hälfte der Parameter nahe.

Im Einzelnen sind die Beiträge dieses Artikels wie folgt:

• 1. Trainierte und veröffentlichte das LLEMMA-Modell: 7B- und 34B-Sprachmodelle für Mathematik. Das LLEMMA-Modell ist der Stand der Technik unter den auf MATH öffentlich veröffentlichten Basismodellen.
• 2. Veröffentlichung von AlgebraicStack, einem Datensatz mit 11B Code-Tokens speziell für Mathematik.
• 3. Es wurde gezeigt, dass LLEMMA in der Lage ist, mathematische Probleme mithilfe von Rechenwerkzeugen zu lösen, nämlich einem Python-Interpreter und einem formalen Theorembeweis.
• 4. Im Gegensatz zu früheren mathematischen Sprachmodellen (wie Minerva) ist das LLEMMA-Modell offen. Die Forscher stellten die Trainingsdaten und den Code der Öffentlichkeit zur Verfügung. Dies macht LLEMMA zu einer Plattform für zukünftige Forschung im Bereich des mathematischen Denkens.

Methodenübersicht

LLEMMA ist ein 70B- und 34B-Sprachmodell, das speziell in der Mathematik verwendet wird. Es wird erhalten, indem der Code Llama weiterhin auf Proof-Pile-2 vorab trainiert wird.

DATEN: Proof-Pile-2

Die Forscher erstellten Proof-Pile-2, eine wissenschaftliche Arbeit mit 55B-Token, Netzwerkdaten mit Mathematik und einer Mischung aus mathematische Codes. Die Wissensfrist für Proof-Pile-2 ist April 2023, mit Ausnahme der Lean-Proofsteps-Untergruppe.

Rechenwerkzeuge wie numerische Simulationen, Computeralgebrasysteme und formale Theorembeweiser werden für Mathematiker immer wichtiger. Daher erstellten die Forscher AlgebraicStack, einen 11B-Token-Datensatz mit Quellcode in 17 Sprachen, der numerische Mathematik, symbolische Mathematik und formale Mathematik abdeckt. Der Datensatz besteht aus gefilterten Codes aus Stack, öffentlichen GitHub-Repositorys und formalen Beweisschrittdaten. Tabelle 9 zeigt die Anzahl der Token für jede Sprache in AlgebraicStack.

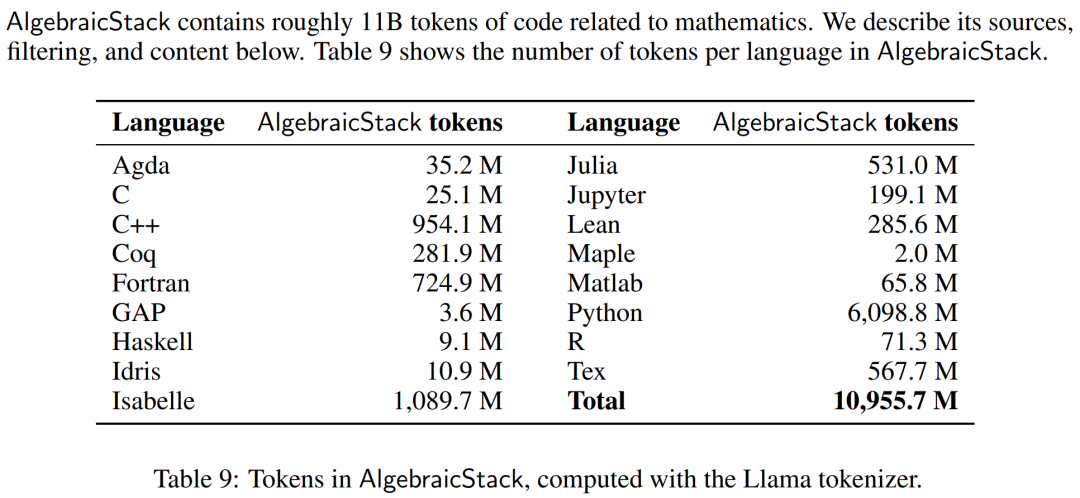
Die Anzahl der Token in jeder Sprache in AlgebraicStack.

Die Forscher verwendeten OpenWebMath, einen 15-B-Token-Datensatz, der aus hochwertigen Webseiten besteht und nach mathematischen Inhalten gefiltert ist. OpenWebMath filtert CommonCrawl-Webseiten basierend auf mathematischen Schlüsselwörtern und klassifikatorbasierten mathematischen Ergebnissen, behält die mathematische Formatierung bei (z. B. LATEX, AsciiMath) und enthält zusätzliche Qualitätsfilter (z. B. Plexität, Domäne, Länge) und Beinahe-Duplikation.

Darüber hinaus verwendeten die Forscher auch die ArXiv-Teilmenge von RedPajama, eine offene Version des LLaMA-Trainingsdatensatzes. Die ArXiv-Teilmenge enthält 29B-Blöcke. Die Trainingsmischung besteht aus einer kleinen Menge allgemeiner Domänendaten und fungiert als Regularisierer. Da der Vortrainingsdatensatz für LLaMA 2 noch nicht öffentlich verfügbar ist, verwendeten die Forscher Pile als alternativen Trainingsdatensatz.

Modell und Training

Jedes Modell wird von Code Llama initialisiert, das wiederum von Llama 2 initialisiert wird, unter Verwendung einer Nur-Decoder-Transformatorstruktur, mit einem 500B-Code-Token. Hergestellt aus Training. Die Forscher trainierten das Code-Llama-Modell weiterhin auf Proof-Pile-2 unter Verwendung des standardmäßigen autoregressiven Sprachmodellierungsziels. Hier verfügt das LLEMMA 7B-Modell über 200B Token und das LLEMMA 34B-Modell über 50B Token.

Die Forscher verwendeten die GPT-NeoX-Bibliothek, um die beiden oben genannten Modelle mit gemischter Präzision bfloat16 auf 256 A100 40-GB-GPUs zu trainieren. Sie verwendeten Tensorparallelität mit Weltgröße 2 für LLEMMA-7B und Tensorparallelität mit Weltgröße 8 für 34B sowie Shard-Optimierungszustände der Stufe 1 von ZeRO über datenparallele Replikate hinweg. Flash Attention 2 wird auch verwendet, um den Durchsatz zu erhöhen und den Speicherbedarf weiter zu reduzieren.

LLEMMA 7B wurde für 42.000 Schritte trainiert, mit einer globalen Stapelgröße von 4 Millionen Token und einer Kontextlänge von 4096 Token. Dies entspricht 23.000 A100-Stunden. Die Lernrate erwärmt sich nach 500 Schritten auf 1·10^−4 und fällt dann nach 48.000 Schritten auf 1/30 der maximalen Lernrate ab.

LLEMMA 34B wurde für 12.000 Schritte trainiert, die globale Stapelgröße beträgt ebenfalls 4 Millionen Token und die Kontextlänge beträgt 4096. Dies entspricht 47.000 A100-Stunden. Die Lernrate erwärmt sich nach 500 Schritten auf 5·10^−5 und fällt dann auf 1/30 der Spitzenlernrate ab.

Bewertungsergebnisse

Im experimentellen Teil wollten die Forscher bewerten, ob LLEMMA als Basismodell für mathematische Texte verwendet werden kann. Sie nutzen die Few-Shot-Auswertung zum Vergleich von LLEMMA-Modellen und konzentrieren sich hauptsächlich auf SOTA-Modelle, die nicht auf überwachte Stichproben mathematischer Aufgaben abgestimmt sind.

Die Forscher verwendeten zunächst Chain-of-Thinking-Argumentation und Mehrheitsentscheidungsmethoden, um die Fähigkeit von LLEMMA zur Lösung mathematischer Probleme zu bewerten. Die Bewertungsmaßstäbe umfassten MATH und GSM8k. Erkunden Sie dann die Verwendung von Few-Shot-Tools und das Beweisen von Theoremen. Abschließend wird der Einfluss der Speicher- und Datenmischung untersucht.

Lösen Sie mathematische Probleme mit Chains of Thoughts (CoT)

Zu diesen Aufgaben gehört das Generieren unabhängiger Textantworten auf Fragen in LATEX oder natürlicher Sprache, ohne dass externe Tools erforderlich sind. Zu den von Forschern verwendeten Bewertungsmaßstäben gehören MATH, GSM8k, OCWCourses, SAT und MMLU-STEM.

Die Ergebnisse sind in Tabelle 1 unten aufgeführt. Das kontinuierliche Vortraining von LLEMMA auf dem Proof-Pile-2-Korpus hat die Leistung bei wenigen Stichproben bei 5 mathematischen Benchmarks verbessert. Darunter hat sich LLEMMA 34B bei GSM8k um 20 Punkte verbessert als Code Llama. Prozentpunkte, 13 Prozentpunkte höher als Code Llama bei MATH. Gleichzeitig übertraf LLEMMA 7B das proprietäre Minerva-Modell.

Daher kamen die Forscher zu dem Schluss, dass kontinuierliches Vortraining auf Proof-Pile-2 dazu beitragen kann, die Fähigkeit des vorab trainierten Modells zur Lösung mathematischer Probleme zu verbessern.

Verwenden Sie Werkzeuge, um mathematische Probleme zu lösen

Zu diesen Aufgaben gehört die Verwendung von Berechnungswerkzeugen, um Probleme zu lösen. Zu den von Forschern verwendeten Bewertungsbenchmarks gehören MATH+Python und GSM8k+Python.

Die Ergebnisse sind in Tabelle 3 unten aufgeführt. LLEMMA übertrifft Code Llama bei beiden Aufgaben. Auch die Leistung auf MATH und GSM8k ist mit beiden Tools besser als ohne die Tools.

Formale Mathematik

Der AlgebraicStack-Datensatz von Proof-Pile-2 enthält 1,5 Milliarden Token formaler mathematischer Daten, einschließlich formaler Beweise, die von Lean und Isabelle extrahiert wurden. Während ein vollständiges Studium der formalen Mathematik den Rahmen dieses Artikels sprengen würde, haben wir die Leistung von LLEMMA bei wenigen Schüssen bei den folgenden beiden Aufgaben bewertet.

Informelle bis formale Beweisaufgabe, das heißt, wenn ein formaler Satz, ein informeller LATEX-Satz und ein informeller LATEX-Beweis gegeben sind, wird ein formaler Beweis generiert;

Form-zu-formeller Beweis , um einen formalen Satz zu beweisen, indem eine Reihe von Beweisschritten (oder Strategien) generiert werden.

Die Ergebnisse sind in Tabelle 4 unten aufgeführt. Das kontinuierliche Vortraining von LLEMMA auf Proof-Pile-2 verbesserte die Leistung bei wenigen Stichproben bei zwei formalen Theorembeweisaufgaben.

Auswirkungen der Datenmischung

Beim Training eines Sprachmodells besteht eine gängige Praxis darin, eine hochwertige Teilmenge der Trainingsdaten basierend auf Mischungsgewichten hochzurechnen. Die Forscher wählten die Mischungsgewichte aus, indem sie ein kurzes Training mit mehreren sorgfältig ausgewählten Mischungsgewichten durchführten. Anschließend wurden Mischgewichte ausgewählt, die die Verwirrung bei einem Satz hochqualitativer vorgehaltener Texte minimierten (hier wurde der MATH-Trainingssatz verwendet).

Tabelle 5 unten zeigt die MATH-Trainingssatz-Perplexität des Modells nach dem Training mit verschiedenen Datenmischungen wie arXiv, Web und Code.

Weitere technische Details und Bewertungsergebnisse finden Sie im Originalpapier.

Das obige ist der detaillierte Inhalt von​Mit fast der Hälfte der Parameter liegt die Leistung nahe an Google Minerva, einem weiteren großen mathematischen Modell, das Open Source ist. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!