Heim >Technologie-Peripheriegeräte >KI >Terence Tao nähert sich einem weiteren 60-jährigen Geometrieproblem! Beim Problem der regelmäßigen Nahtpflasterung wurde ein neuer Durchbruch erzielt
Terence Tao nähert sich einem weiteren 60-jährigen Geometrieproblem! Beim Problem der regelmäßigen Nahtpflasterung wurde ein neuer Durchbruch erzielt
- PHPznach vorne
- 2023-10-14 14:17:071154Durchsuche
Tao Zhexuan hat einen neuen Durchbruch bei der Untersuchung des periodischen Kachelproblems erzielt
Am 18. September haben Tao Zhexuan und Rachel Greenfeld das Preprint-Papier „Undecidability of translatoral monotilings“ auf arXiv hochgeladen.

Papieradresse: https://arxiv.org/abs/2309.09504
Die Hauptschlussfolgerung dieses Papiers ist, dass, wenn die Dimension des Gitters unbegrenzt ist, dann die endliche Unterteilung des Gitters bestimmt werden muss Die Frage, ob eine Menge eine periodische Teilmenge des Gitters kacheln kann, ist unentscheidbar
Wissen Sie, dieses Problem ist in Dimension 1 und Dimension 2 entscheidbar.
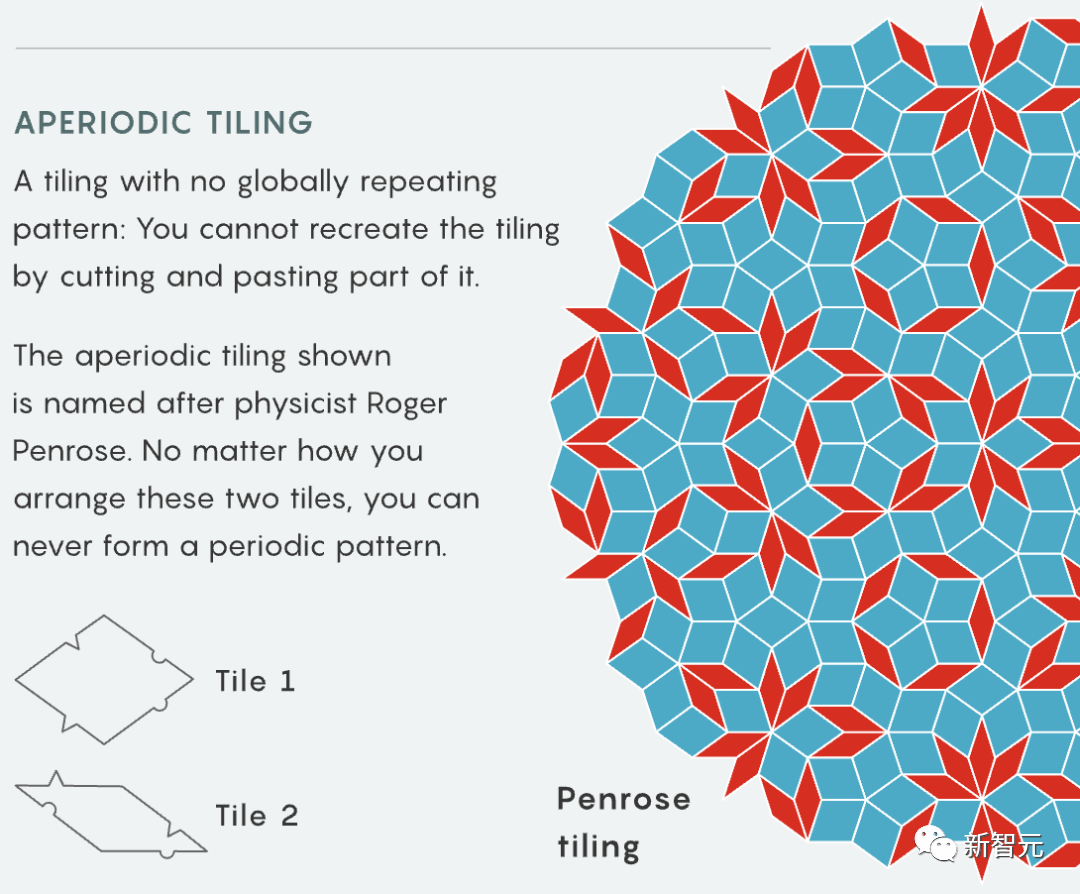
Tao Zhexuan sagte, es sei etwas seltsam, dass die meisten der in dem Artikel gezeigten Komponenten beliebten Spielen ähneln –
Die Kachelanaloga von Domino, Sudoku, dem Computerspiel „Tetris““ , sogar das Kinderspiel „Fizz Buzz“ erschien
Warum erfordert das Lernen einer Matheaufgabe so viele Spiele? Tao Zhexuan kann auch die Unentscheidbarkeit der translatorischen einzelnen dichten Kacheln nicht erklären. Dieser Artikel ist eine Fortsetzung des vorherigen Artikels der beiden. Link Periodic Tile Problem

In der letzten Arbeit konstruierten sie eine translatorische einzelne dichte Kachelung eines hochdimensionalen Gitters
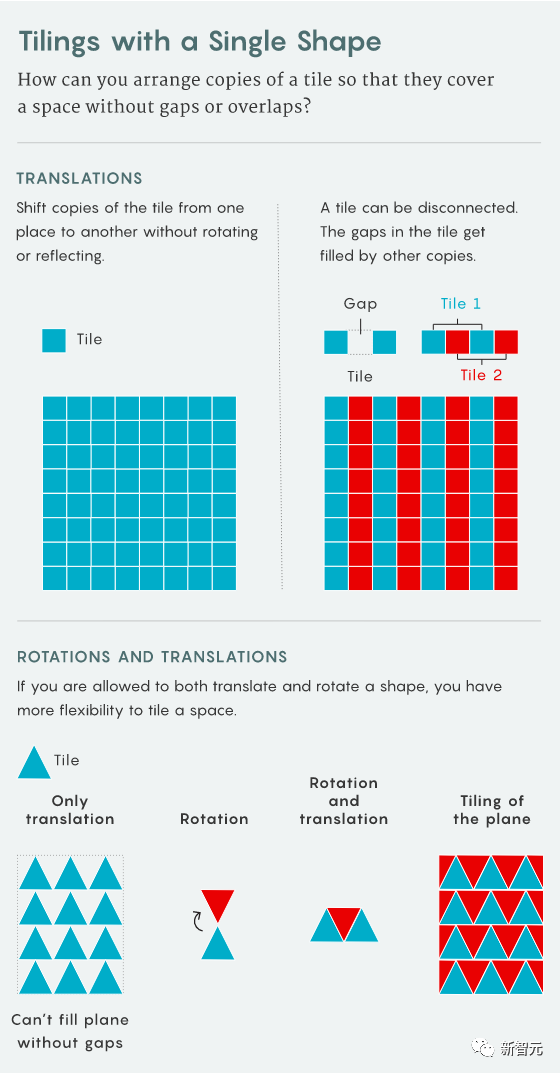
(eine einzelne dichte Kachelung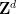 ist also ein endliche Menge), es ist nicht periodisch (es gibt keine Möglichkeit, diese Kachelung in eine periodische Kachelung zu „fixieren“
ist also ein endliche Menge), es ist nicht periodisch (es gibt keine Möglichkeit, diese Kachelung in eine periodische Kachelung zu „fixieren“ 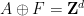 , wobei
, wobei
ist). 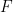
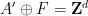
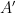 Diese Tatsache widerlegt die Hypothese von Stein, Grunbaum-Shephard und Lagarias-Wang über die Nichtexistenz aperiodischer dicht gepackter Monomere
Diese Tatsache widerlegt die Hypothese von Stein, Grunbaum-Shephard und Lagarias-Wang über die Nichtexistenz aperiodischer dicht gepackter Monomere 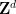 („Hat single dicht gepackt“ ist ein kürzlich entdecktes aperiodisches isometrisches Single dichte Kacheln
(„Hat single dicht gepackt“ ist ein kürzlich entdecktes aperiodisches isometrisches Single dichte Kacheln
, bei denen Drehung, Reflexion und Translation zulässig sind, oder der neuere „Geistermonolith“ ähnelt der einzelnen dichten Kachelung, ist jedoch nicht erforderlich. 
Einer der Gründe, warum Tao Zhexuan und Rachel Greenfeld diese Vermutung inspirierten, ist die Beobachtung des Mathematikers Hao Wang
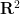 Er fand heraus, dass, wenn die periodische Kachelvermutung wahr ist, das translatorische Kachelproblem algorithmisch bestimmbar ist ——
Er fand heraus, dass, wenn die periodische Kachelvermutung wahr ist, das translatorische Kachelproblem algorithmisch bestimmbar ist ——
Es gibt eine Turingmaschine für 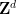 , bei gegebener Dimension
, bei gegebener Dimension 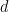 und einer endlichen Teilmenge
und einer endlichen Teilmenge 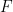 kann in begrenzter Zeit bestimmt werden, ob
kann in begrenzter Zeit bestimmt werden, ob 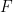 tesseliert werden kann
tesseliert werden kann 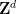 . Das liegt daran, dass periodische Kacheln über eine Computersuche gefunden werden können subs Mengen, diese Teilmengen können nicht durch
. Das liegt daran, dass periodische Kacheln über eine Computersuche gefunden werden können subs Mengen, diese Teilmengen können nicht durch
disjunkte Übersetzungen abgedeckt werden, die auch durch Computersuche entdeckt werden können.
Die periodische Tessellationsvermutung besagt, dass dies die einzigen zwei möglichen Situationen sind, und gibt somit Entscheidbarkeit vor. 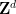
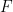 Andererseits ist Wangs Standpunkt unveränderlich: Das Scheitern der periodischen Tessellationsvermutung bedeutet nicht automatisch die Unentscheidbarkeit des translatorischen Einzeltessellationsproblems, da es die Existenz anderer Algorithmen nicht ausschließt Bestimmen Sie die Tessellation. Diese Tessellation kann unabhängig von der Existenz einer periodischen Tessellation sein
Andererseits ist Wangs Standpunkt unveränderlich: Das Scheitern der periodischen Tessellationsvermutung bedeutet nicht automatisch die Unentscheidbarkeit des translatorischen Einzeltessellationsproblems, da es die Existenz anderer Algorithmen nicht ausschließt Bestimmen Sie die Tessellation. Diese Tessellation kann unabhängig von der Existenz einer periodischen Tessellation sein
(zum Beispiel auch mit der neu entdeckten Hut- und Geister-Tessellation für den isometrischen Simplex von Polygonen mit rationalen Koeffizienten in
Es bleibt offen Frage, ob das Problem der dichten Kachelung mit oder ohne Reflexion entscheidbar ist 
Die Hauptergebnisse dieser Arbeit befassen sich mit diesem Problem (mit einer Einschränkung):
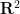 Der schriftliche Inhalt ist: Satz 1
Der schriftliche Inhalt ist: Satz 1
Es gibt keinen Algorithmus für

, einer periodischen Teilmenge
und einer endlichen Teilmenge. Bestimmen Sie, ob ein Schwenken vorliegt Es ist wichtig zu beachten, dass man eine periodische Teilmenge Darüber hinaus bemerkten Terence Tao und Rachel Greenfeld auch, dass bei Für jeden festen Wert von Aufgrund des bekannten Zusammenhangs zwischen algorithmischer Unentscheidbarkeit und logischer Unentscheidbarkeit (auch als logische Unabhängigkeit bekannt) impliziert dieser Satz auch die Existenz einer (im Prinzip eindeutig beschreibbaren) Dimension Aufgrund dieses Ansatzes können wir Beschreiben Sie als Nächstes einige der Hauptgedanken des Beweises. Eine übliche Methode, um zu beweisen, dass ein Problem unentscheidbar ist, besteht darin, andere Probleme, von denen bekannt ist, dass sie unentscheidbar sind, in das ursprüngliche Problem zu „kodieren“, sodass jeder Algorithmus, der das ursprüngliche Problem bestimmt, auch das eingebettete Problem bestimmen kann Deshalb kodieren wir das Wang-Dense-Shop-Problem als ein einzelnes Dense-Shop-Problem Das zweite Problem betrifft das Wang-Dense-Shop-Problem Gegeben ein endliches Wang For a Satz von Kacheln
Gegeben sei eine endliche Menge horizontaler (oder vertikaler) Dominosteine oder einen Punkt zuzuweisen, sodass jedes Paar in dieser Kachel horizontale (oder vertikale) Quadrate aus verwenden kann oder ? Aufgabe 4 (Sudoku-Aufgabe) Gegeben ist die Spaltenbreite Der neuartigste Teil dieser Arbeit ist der Beweis, dass das Domino-Problem tatsächlich in ein Sudoku-Problem eingebettet werden kann. Die Einbettung des Sudoku-Problems in ein einziges geheimes Rätsel basiert auf der modifizierten Methode, die in früheren Artikeln vorgeschlagen wurde. „Padding Language“ kann verschiedene Probleme (einschließlich Sudoku-Probleme) in ein einziges Paving-Problem umwandeln. Um das Domino-Problem in ein Sudoku-Problem zu kodieren, müssen wir eine Domino-Funktion erhalten ein Domino-Set ) und verwenden Sie es, um eine Sudoku-Funktion zu erstellen Dieser Ansatz ist nicht sofort offensichtlich, aber Tao und Rachel Greenfeld haben mit Hilfe von Emmanuel Jeandel einige Ideen von Aanderaa und Lewis übernommen und bestimmte Hierarchien verwendet, um ein Problem in ein anderes zu kodieren. Hier erklären wir die hierarchische Struktur Dann bauen Sie die Sudoku-Funktion wobei und Das typische Beispiel für das Endgewicht Interessanterweise aus irgendeinem Grund Die Dekoration folgt hier grundsätzlich den Regeln des Kinderspiels „Fizz Buzz“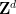 im Inneren eine begrenzte Zeit
im Inneren eine begrenzte Zeit 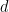
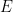
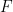 .
.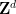 von
von 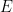 und nicht alle
und nicht alle 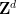 verwenden muss; dies liegt größtenteils an den technischen Einschränkungen dieses Ansatzes und lässt sich wahrscheinlich durch zusätzlichen Aufwand und Kreativität erreichen zu beseitigen.
verwenden muss; dies liegt größtenteils an den technischen Einschränkungen dieses Ansatzes und lässt sich wahrscheinlich durch zusätzlichen Aufwand und Kreativität erreichen zu beseitigen. 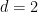 die periodische Pflastervermutung von Bhattacharya aufgestellt wurde, sodass das Problem in diesem Fall entscheidbar ist
die periodische Pflastervermutung von Bhattacharya aufgestellt wurde, sodass das Problem in diesem Fall entscheidbar ist 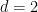 .
. 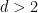 ist noch offen, ob das Kachelproblem entscheidbar ist (beachten Sie, dass im obigen Ergebnis die Dimension
ist noch offen, ob das Kachelproblem entscheidbar ist (beachten Sie, dass im obigen Ergebnis die Dimension 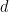 nicht fest, sondern Teil der Eingabe ist).
nicht fest, sondern Teil der Eingabe ist). 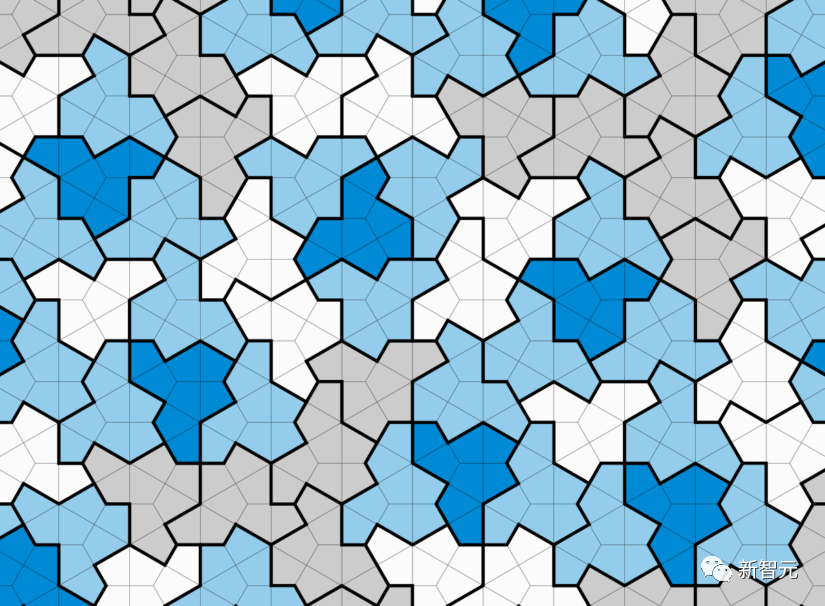
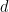 Der periodischen Teilmengen
Der periodischen Teilmengen 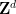 von ,
von , 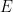 und die endliche Teilmenge
und die endliche Teilmenge 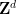 von
von 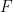 lassen
lassen 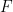 die Übersetzungskachelung
die Übersetzungskachelung 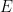 bestehen und können in der ZFC-Mengentheorie weder bestätigt noch verfälscht werden (natürlich vorausgesetzt, die Theorie ist konsistent).
bestehen und können in der ZFC-Mengentheorie weder bestätigt noch verfälscht werden (natürlich vorausgesetzt, die Theorie ist konsistent).  hier auch durch die „fast zweidimensionale“ Gruppe
hier auch durch die „fast zweidimensionale“ Gruppe 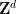 ersetzen, wobei
ersetzen, wobei 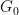 eine endliche abelsche Gruppe ist (jetzt Teil der Eingabe, stattdessen Dimensionen).
eine endliche abelsche Gruppe ist (jetzt Teil der Eingabe, stattdessen Dimensionen). 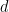 ).
). 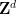 :
: 
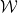 (Einheitsquadrate, jeder Kante ist eine bestimmte Farbe aus einer begrenzten Palette zugewiesen), ist es möglich, die Ebene mithilfe eines Standardgitters
(Einheitsquadrate, jeder Kante ist eine bestimmte Farbe aus einer begrenzten Palette zugewiesen), ist es möglich, die Ebene mithilfe eines Standardgitters 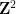 durch Übersetzung so zu tesselisieren, dass benachbarte Kacheln auf einer gemeinsamen Fläche die gleiche Farbe haben? Rand? Berger hat einmal die berühmte Schlussfolgerung gezogen, dass dieses Problem nicht bestimmt werden kann Das Problem der dimensionalen Übersetzung einzelner dichter Kacheln muss einige Zwischenprobleme lösen
durch Übersetzung so zu tesselisieren, dass benachbarte Kacheln auf einer gemeinsamen Fläche die gleiche Farbe haben? Rand? Berger hat einmal die berühmte Schlussfolgerung gezogen, dass dieses Problem nicht bestimmt werden kann Das Problem der dimensionalen Übersetzung einzelner dichter Kacheln muss einige Zwischenprobleme lösen 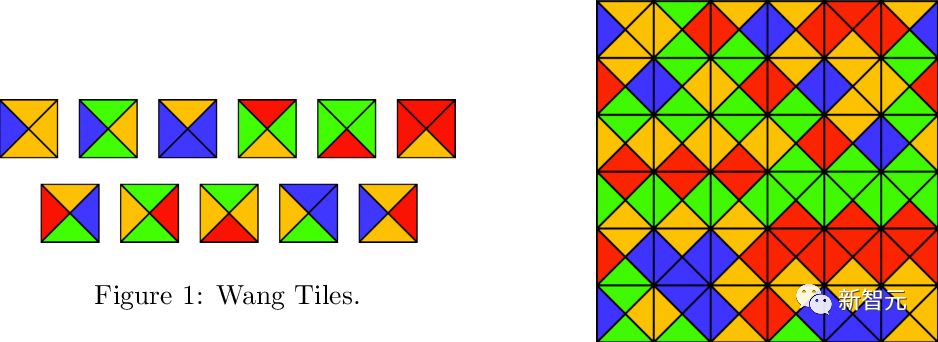 Zunächst können wir das Problem der dichten Kachelung nach Wang leicht in ein ähnliches Problem einbetten, das wir Domino-Problem nennen:
Zunächst können wir das Problem der dichten Kachelung nach Wang leicht in ein ähnliches Problem einbetten, das wir Domino-Problem nennen: 

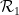
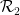 Tatsächlich müssen wir nur jede Wang-Kachel als separaten „Punkt“ einfügen und das Domino-Set
Tatsächlich müssen wir nur jede Wang-Kachel als separaten „Punkt“ einfügen und das Domino-Set 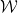 ,
, 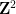 so definieren, dass es horizontal oder vertikal aneinander angrenzt und die Kanten Paare von Wang-Geheimnissen aufweisen der gleichen Farbe.
so definieren, dass es horizontal oder vertikal aneinander angrenzt und die Kanten Paare von Wang-Geheimnissen aufweisen der gleichen Farbe. 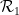 In den nächsten Schritten kombinieren wir das Domino-Problem mit dem Sudoku-Problem:
In den nächsten Schritten kombinieren wir das Domino-Problem mit dem Sudoku-Problem: 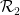

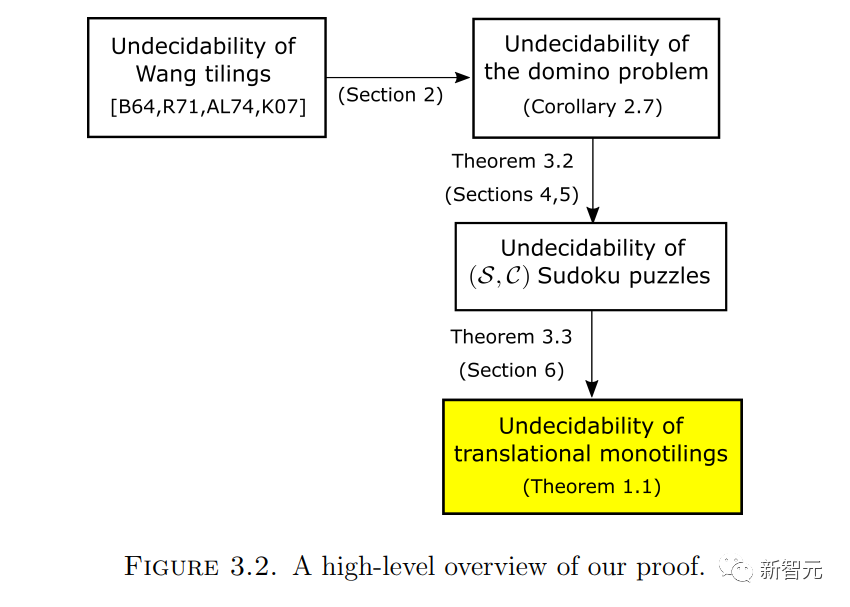
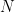 , die Menge der Zahlen
, die Menge der Zahlen 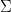 , die Menge der Funktionen
, die Menge der Funktionen 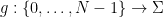
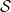 und die „Ausgangsbedingungen“
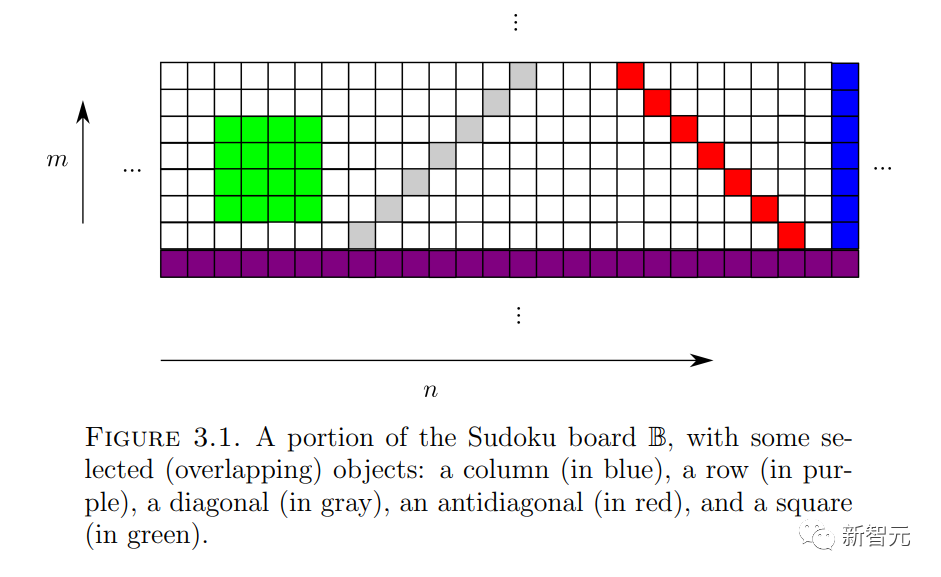
und die „Ausgangsbedingungen“ 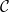 ( Hier möchte ich nicht auf Details eingehen): Ist es möglich, jeder Zelle
( Hier möchte ich nicht auf Details eingehen): Ist es möglich, jeder Zelle 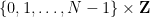 im „Sudoku-Brett“
im „Sudoku-Brett“ 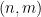 eine Nummer
eine Nummer 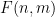 zuzuweisen, sodass für jede Steigung
zuzuweisen, sodass für jede Steigung 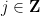 und jeden Schnittpunkt
und jeden Schnittpunkt 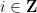 Befinden sich die Zahlen
Befinden sich die Zahlen 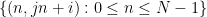 entlang der
entlang der 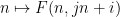 -Linie in
-Linie in 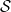 (und
(und 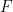 gehorchen die Anfangsbedingungen
gehorchen die Anfangsbedingungen 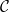 )?
)? 
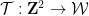 (befolgen Sie einige mit dem Domino-Set verbundene Sudoku-Einschränkungen); umgekehrt gehorcht jede der Zahl. Die Sudoku-Funktionen der Sudoku-Rätselregeln müssen aus dem Domino generiert werden irgendwie funktionieren.
(befolgen Sie einige mit dem Domino-Set verbundene Sudoku-Einschränkungen); umgekehrt gehorcht jede der Zahl. Die Sudoku-Funktionen der Sudoku-Rätselregeln müssen aus dem Domino generiert werden irgendwie funktionieren. 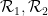
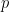 (aufgrund der Zweidimensionalität des Dominoproblems müssen zwei verschiedene Primzahlen verwendet werden).
(aufgrund der Zweidimensionalität des Dominoproblems müssen zwei verschiedene Primzahlen verwendet werden). 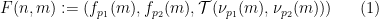 mit
mit 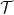 über die Formel
über die Formel 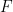 auf, die eine Art Einbettung verkörpert.
auf, die eine Art Einbettung verkörpert. 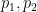 zwei verschiedene große Primzahlen sind (zum Beispiel können Sie
zwei verschiedene große Primzahlen sind (zum Beispiel können Sie 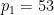 ,
, 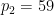 nehmen),
nehmen), 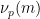 die Häufigkeit darstellt, mit der
die Häufigkeit darstellt, mit der 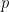 durch
durch 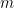 geteilt wird, und.
geteilt wird, und. 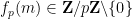 ist die letzte Zahl ungleich Null in der Erweiterung von
ist die letzte Zahl ungleich Null in der Erweiterung von 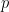 :
: 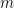
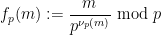 (
(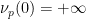 ). Im Fall von 情况 ist die erste Komponente von (1) unten dargestellt:
). Im Fall von 情况 ist die erste Komponente von (1) unten dargestellt: 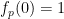
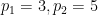 ist unten dargestellt:
ist unten dargestellt: 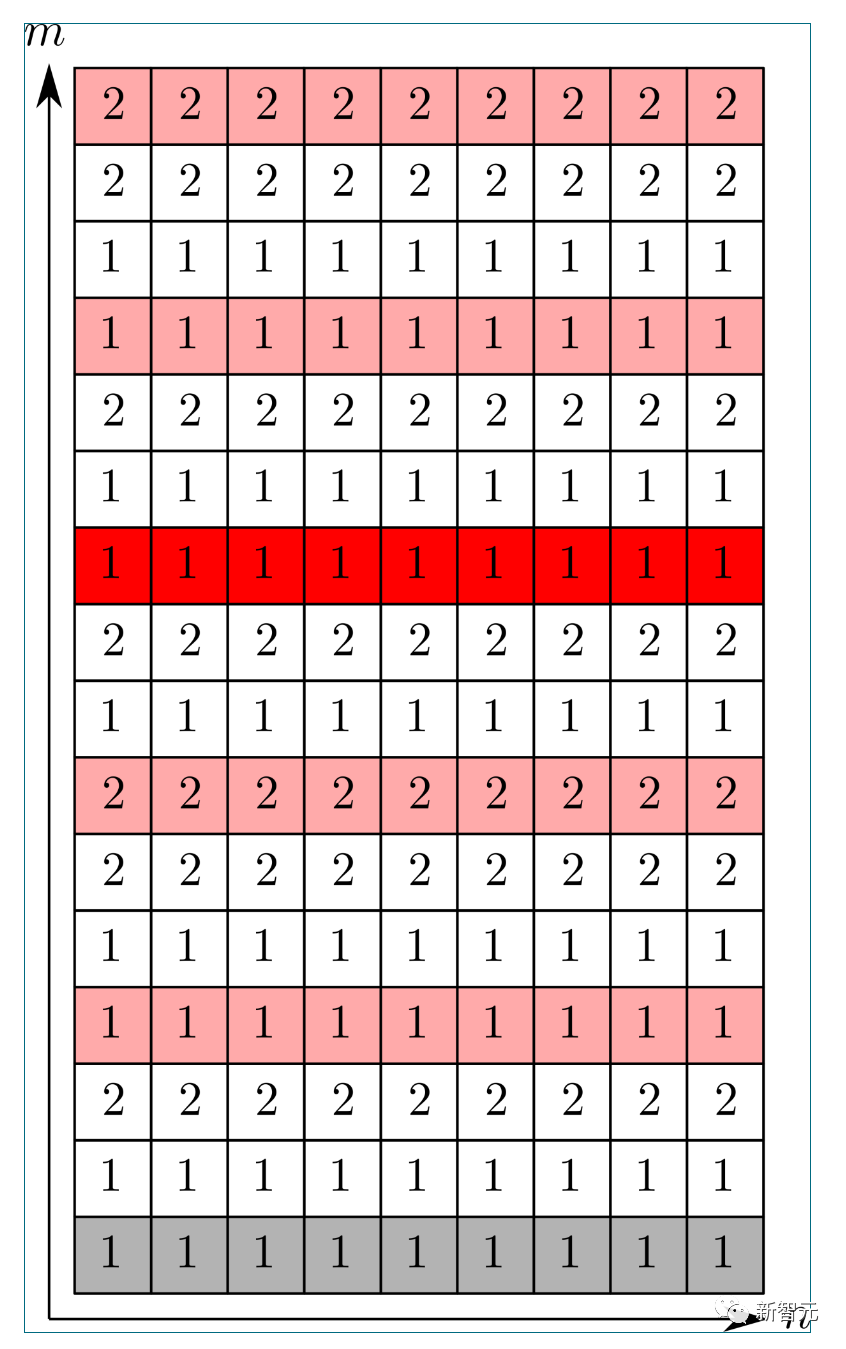
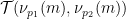
Das obige ist der detaillierte Inhalt vonTerence Tao nähert sich einem weiteren 60-jährigen Geometrieproblem! Beim Problem der regelmäßigen Nahtpflasterung wurde ein neuer Durchbruch erzielt. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- 4 Tipps zur Verwendung der Ersatzfunktion beim Erlernen von Excel-Funktionen
- Google löst das Problem der Speicherung und Bearbeitung n-dimensionaler Daten mit einer Open-Source-Softwarebibliothek
- GPT-4 verfügt über großartige mathematische Fähigkeiten! Die explosive Forschung von OpenAI zum Thema „Prozessüberwachung' durchbricht 78,2 % der Probleme und beseitigt Halluzinationen
- Weltneuheit: Der neue KI-Algorithmus von Molecular Heart zur Überwindung der Probleme der Proteinseitenkettenvorhersage und des Sequenzdesigns

