Zerlegung multimodaler Verteilungen mithilfe von Gaußschen Mischungsmodellen

Die eindimensionale multimodale Verteilung kann mithilfe des Gaußschen Mischungsmodells in mehrere Verteilungen aufgeteilt werden.

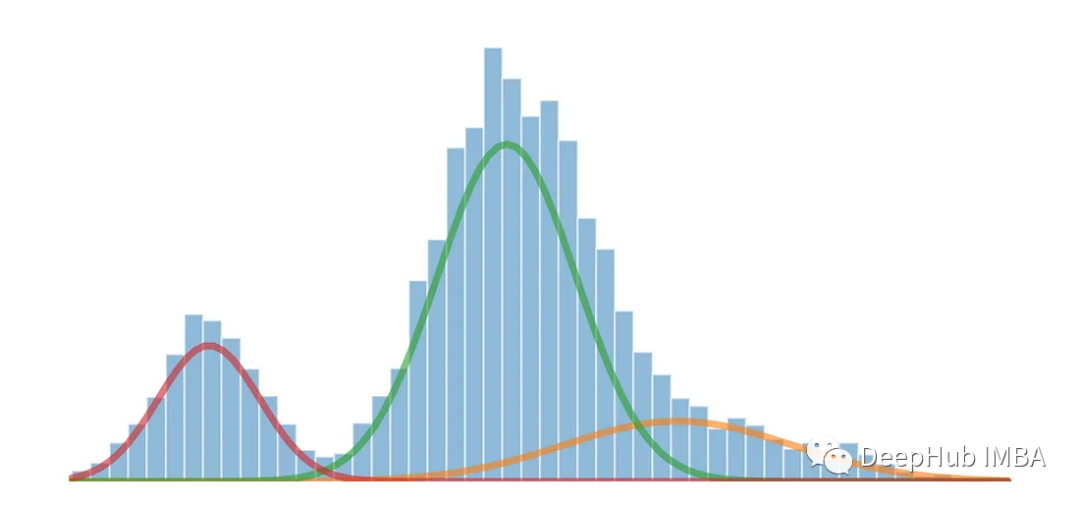
Gaußsche Mischungsmodelle (GMM) sind eine häufig verwendete Methode in den Bereichen Statistik und maschinelles Lernen Analyse komplexer Datenverteilungen. GMM ist ein generatives Modell, das davon ausgeht, dass die beobachteten Daten aus mehreren Gaußschen Verteilungen bestehen. Jede Gaußsche Verteilung wird als Komponente bezeichnet und diese Komponenten steuern ihren Beitrag zu den Daten durch Gewichte.

Generieren Sie Daten mit multimodalen Verteilungen

Wenn ein Datensatz mehrere verschiedene Peaks oder Modi aufweist, bedeutet dies normalerweise, dass der Datensatz mehrere markante Cluster oder Konzentrationen von Datenpunkten enthält. Jeder Modus stellt einen markanten Cluster oder eine Konzentration von Datenpunkten in der Verteilung dar und kann als hochdichter Bereich betrachtet werden, in dem Datenwerte mit größerer Wahrscheinlichkeit auftreten.

Wir werden ein von Numpy generiertes eindimensionales Array verwenden .

import numpy as np  dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500)  multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)

Lassen Sie uns die eindimensionale Datenverteilung visualisieren.

import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid')  plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()

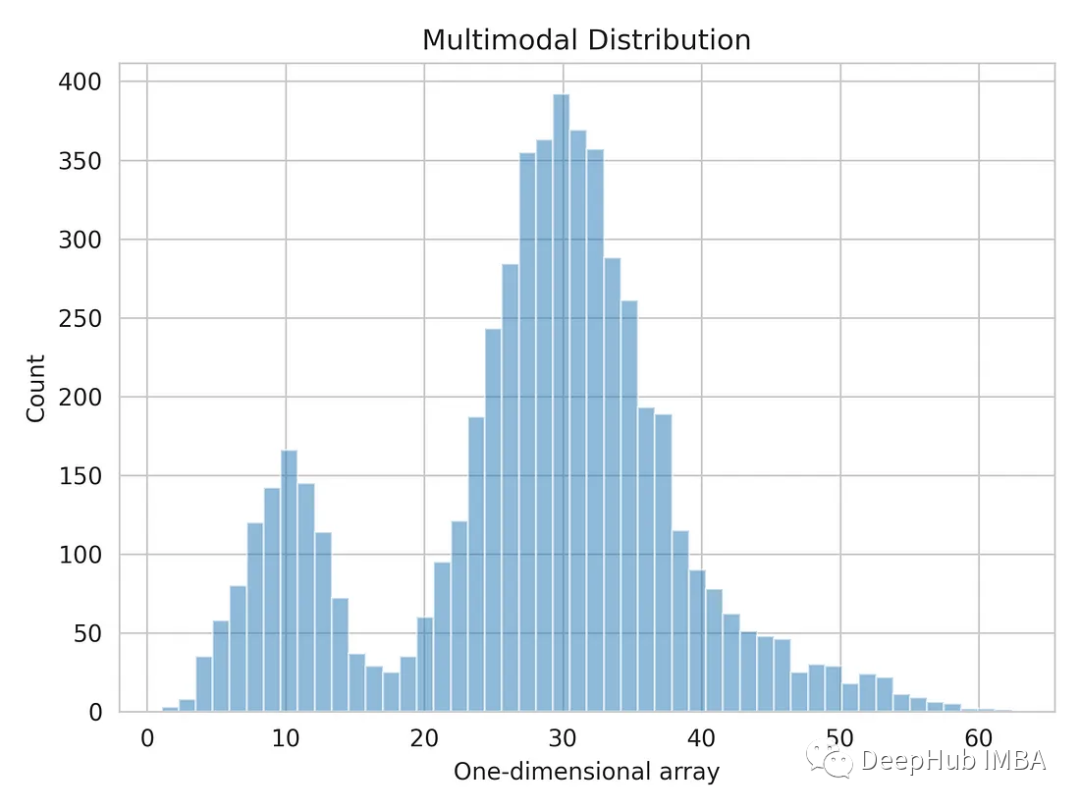
Multimodale Verteilung mithilfe des Gaußschen Mischungsmodells aufteilen

Wir werden das Gaußsche Mischungsmodell verwenden, um den Mittelwert und die Standardabweichung jeder Verteilung zu berechnen, um die multimodale Verteilung in drei Originalverteilungen aufzuteilen. Das Gaußsche Mischungsmodell ist ein unbeaufsichtigtes Wahrscheinlichkeitsmodell, das für die Datenclusterung verwendet werden kann. Es verwendet den Erwartungsmaximierungsalgorithmus, um den Dichtebereich zu schätzen

from sklearn.mixture import GaussianMixture  gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1))  means = gmm.means_  # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5  # Useful when plotting the distributions later weights = gmm.weights_   print(f"Means: {means}, Standard Deviations: {standard_deviations}")  #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]

Wir haben bereits den Mittelwert und die Standardabweichung, um die ursprüngliche Verteilung zu modellieren. Sie sehen, dass der Mittelwert und die Standardabweichung zwar möglicherweise nicht genau korrekt sind, aber eine genaue Schätzung liefern.

Vergleichen Sie unsere Schätzungen mit den Originaldaten.

from scipy.stats import norm  fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))  for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):axes[0].hist(dist, bins=bins, alpha=0.5)  axes[1].hist(multimodal_dist, bins=50, alpha=0.5)  x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)  for mean, covariance, weight in zip(means, standard_deviations, weights):pdf = weight*norm.pdf(x, mean, std)plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)  plt.show()

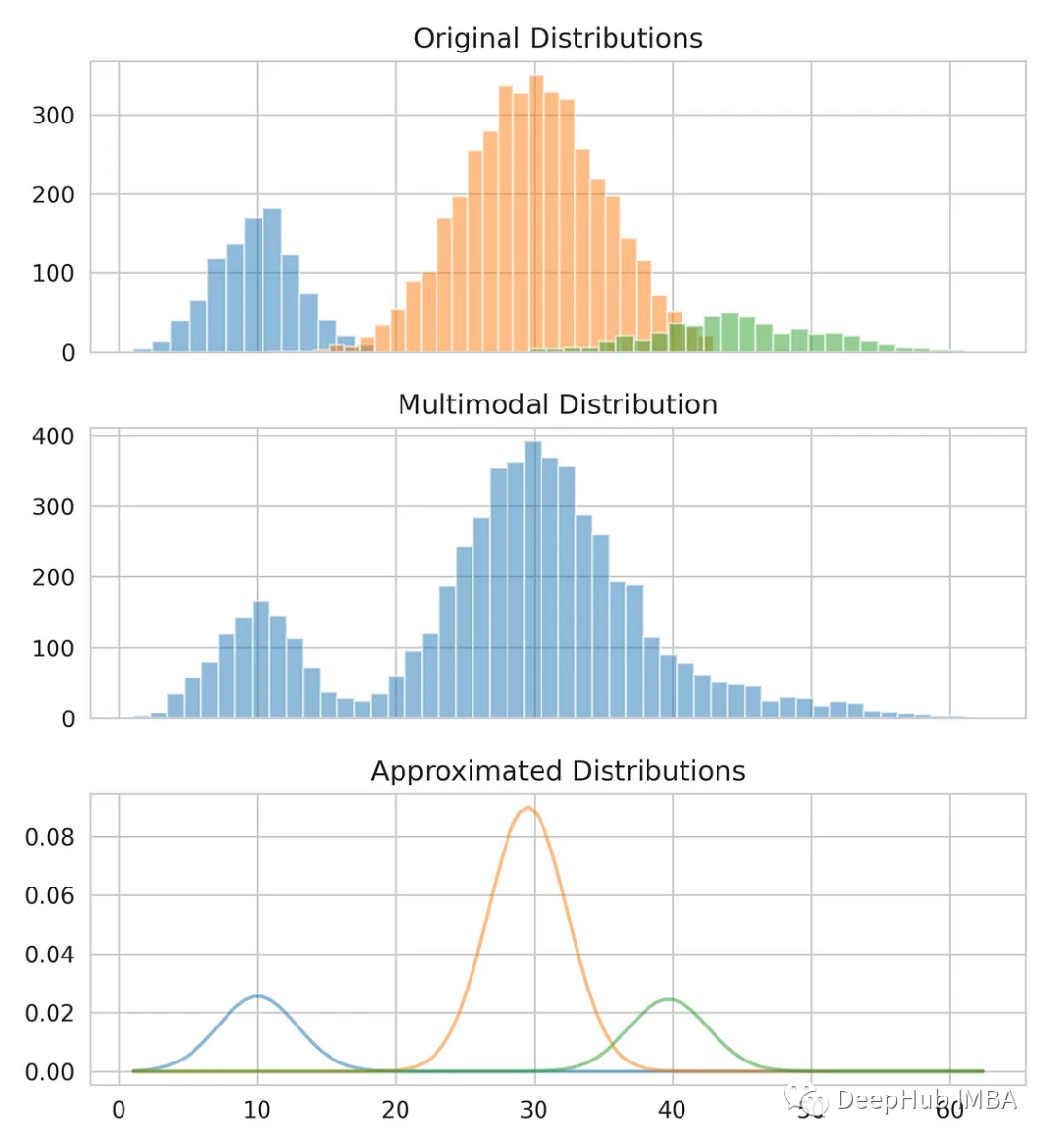
Zusammenfassung

Das Gaußsche Mischungsmodell ist ein leistungsstarkes Werkzeug, mit dem komplexe Datenverteilungen modelliert und analysiert werden können, und ist auch eine der Grundlagen vieler Algorithmen für maschinelles Lernen. Es hat ein breites Anwendungsspektrum und kann verschiedene Datenmodellierungs- und Analyseprobleme lösen

Diese Methode kann als Feature-Engineering-Technik verwendet werden, um die Konfidenzintervalle von Unterverteilungen innerhalb von Eingabevariablen zu schätzen

Das obige ist der detaillierte Inhalt vonZerlegung multimodaler Verteilungen mithilfe von Gaußschen Mischungsmodellen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!