Heim >Technologie-Peripheriegeräte >KI >Quantenmaschinelles Lernen über Kernel-Methoden hinaus, ein einheitliches Framework für Quantenlernmodelle
Quantenmaschinelles Lernen über Kernel-Methoden hinaus, ein einheitliches Framework für Quantenlernmodelle
- PHPznach vorne
- 2023-05-06 17:28:091289Durchsuche
Algorithmen des maschinellen Lernens, die auf parametrisierten Quantenschaltkreisen basieren, sind erstklassige Kandidaten für kurzfristige Anwendungen auf verrauschten Quantencomputern. In dieser Richtung wurden verschiedene Arten von Quantenmaschinenlernmodellen eingeführt und eingehend untersucht. Unser Verständnis darüber, wie diese Modelle miteinander und mit klassischen Modellen verglichen werden, bleibt jedoch begrenzt.
Kürzlich hat ein Forschungsteam der Universität Innsbruck, Österreich, ein konstruktives Framework identifiziert, das alle Standardmodelle basierend auf parametrisierten Quantenschaltkreisen erfasst: das lineare Quantenmodell.
Forscher zeigen, wie mithilfe von Werkzeugen der Quanteninformationstheorie Schaltkreise zum erneuten Hochladen von Daten effizient in ein einfacheres Bild eines linearen Modells im Quanten-Hilbert-Raum abgebildet werden können. Darüber hinaus wird der experimentell relevante Ressourcenbedarf dieser Modelle im Hinblick auf die Anzahl der Qubits und die Menge der zu erlernenden Daten analysiert. Aktuelle Ergebnisse auf Basis des klassischen maschinellen Lernens zeigen, dass lineare Quantenmodelle viel mehr Qubits verwenden müssen als Daten-Reupload-Modelle, um bestimmte Lernaufgaben zu lösen, während Kernel-Methoden auch viel mehr Datenpunkte erfordern. Die Ergebnisse liefern ein umfassenderes Verständnis der Modelle des Quantenmaschinellen Lernens sowie Einblicke in die Kompatibilität verschiedener Modelle mit NISQ-Einschränkungen.
Die Forschung trug den Titel „Quantum Machine Learning Beyond Kernel Methods“ und wurde am 31. Januar 2023 in „Nature Communications“ veröffentlicht.
Link zum Papier: https://www.nature.co m/articles/s41467-023-36159-y
Zwischenquantum (NISQ) In dieser Ära wurden mehrere Methoden vorgeschlagen, um nützliche Quantenalgorithmen zu erstellen, die mit geringfügigen Hardwareeinschränkungen kompatibel sind. Die meisten dieser Methoden beinhalten die Spezifikation von Ansatz-Quantenschaltungen, die auf klassische Weise zur Lösung spezifischer Rechenaufgaben optimiert werden. Neben Variationsquantensignaturlösern und Varianten von Quantennäherungsoptimierungsalgorithmen in der Chemie gehören maschinelle Lernverfahren auf Basis solcher parametrisierter Quantenschaltkreise zu den vielversprechendsten praktischen Anwendungen zur Generierung von Quantenvorteilen.
Kernel-Methoden sind eine Art Mustererkennungsalgorithmus. Sein Zweck besteht darin, die gegenseitigen Beziehungen in einem Datensatz zu finden und zu lernen. Die Kernel-Methode ist eine effektive Methode zur Lösung nichtlinearer Musteranalyseprobleme. Ihre Kernidee besteht darin, zunächst die Originaldaten durch eine nichtlineare Zuordnung in einen geeigneten hochdimensionalen Merkmalsraum einzubetten und dann einen allgemeinen linearen Lernmodus zu verwenden und Verarbeitung im Raum.
Frühere Arbeiten haben in dieser Richtung große Fortschritte gemacht, indem sie die Verbindung zwischen einigen Quantenmodellen und Kernelmethoden des klassischen maschinellen Lernens ausgenutzt haben. Viele Quantenmodelle funktionieren tatsächlich, indem sie Daten in einem hochdimensionalen Hilbert-Raum kodieren und Eigenschaften der Daten modellieren, indem sie nur in diesem Merkmalsraum ausgewertete innere Produkte verwenden. So funktioniert auch die nukleare Methode.
Basierend auf dieser Ähnlichkeit kann eine bestimmte Quantenkodierung verwendet werden, um zwei Arten von Modellen zu definieren: (a) explizite Quantenmodelle, bei denen die kodierten Datenpunkte anhand von Variationsobservablen gemessen werden, die ihre Bezeichnungen angeben; Implizites Kernel-Modell, bei dem ein gewichtetes inneres Produkt codierter Datenpunkte zum Zuweisen von Beschriftungen verwendet wird. In der Literatur zum Quantenmaschinellen Lernen wird großer Wert auf implizite Modelle gelegt.
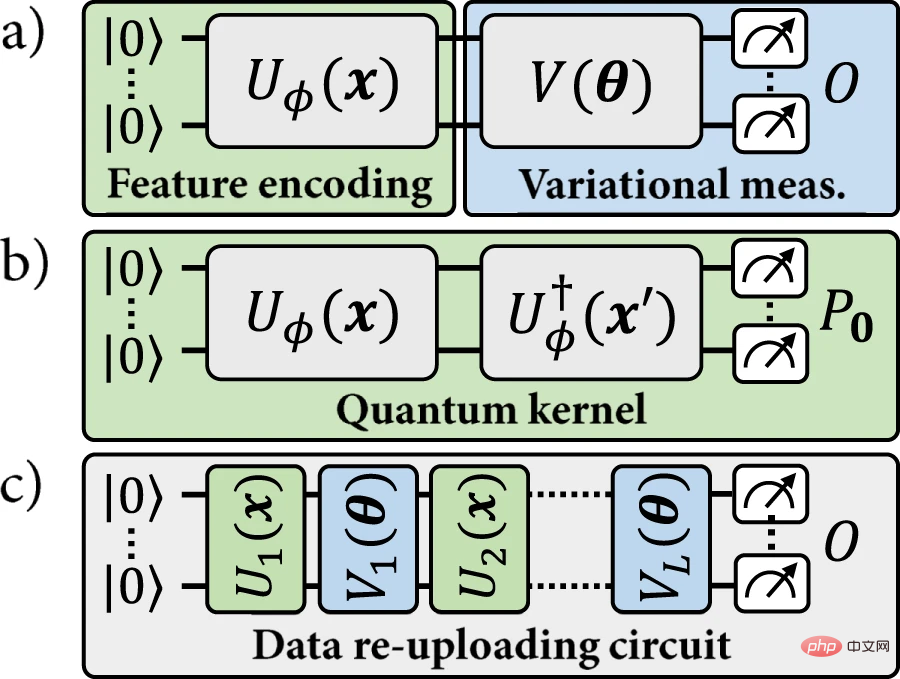
Abbildung 1: Das in dieser Arbeit untersuchte Modell des Quantenmaschinellen Lernens. (Quelle: Papier)
In letzter Zeit gab es Fortschritte bei sogenannten Daten-Re-Upload-Modellen. Das Modell zum erneuten Hochladen von Daten kann als Verallgemeinerung des expliziten Modells angesehen werden. Diese Verallgemeinerung bricht jedoch auch die Übereinstimmung mit dem impliziten Modell, da ein gegebener Datenpunkt x nicht mehr einem festen Kodierungspunkt ρ(x) entspricht. Modelle zum erneuten Hochladen von Daten sind grundsätzlich allgemeiner als explizite Modelle und nicht mit dem Kernel-Modellparadigma kompatibel. Bisher bleibt die Frage offen, ob mit der Garantie von Kernel-Methoden einige Vorteile aus Modellen zum erneuten Hochladen von Daten erzielt werden können.
In dieser Arbeit stellen Forscher ein einheitliches Framework für explizite, implizite und Daten-Re-Upload-Quantenmodelle vor.
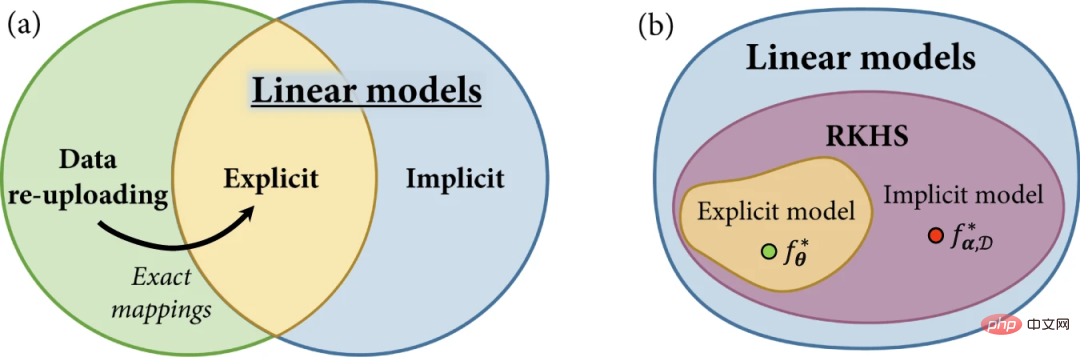
Abbildung 2: Modellfamilie im Quantenmaschinellen Lernen. (Quelle: Paper)
Unified Framework for Quantum Learning Models
Beginnen Sie mit der Überprüfung des Konzepts linearer Quantenmodelle und der Erläuterung expliziter und impliziter Modelle anhand linearer Modelle, die im Quantenmerkmalsraum definiert sind. Anschließend werden Modelle zum erneuten Hochladen von Daten vorgestellt und gezeigt, dass sie, obwohl sie als Verallgemeinerungen expliziter Modelle definiert sind, auch durch lineare Modelle in größeren Hilbert-Räumen implementiert werden können.
Lineares Quantenmodell
Die folgende Abbildung zeigt eine anschauliche Struktur, um visuell zu veranschaulichen, wie die Zuordnung vom erneuten Hochladen der Daten zum expliziten Modell erreicht wird.
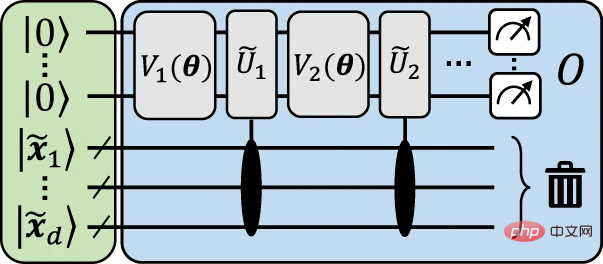
Abbildung 3: Illustratives explizites Modell zur Annäherung an die Schaltung zum erneuten Hochladen von Daten. (Quelle: Paper)
Die allgemeine Idee hinter dieser Struktur besteht darin, die Eingabedaten zu kodieren.
Wir gehen nun zur Hauptstruktur über, was zum erneuten Hochladen der Daten und einer präzisen Zuordnung zwischen expliziten Modellen führt. Basierend auf einer ähnlichen Idee wie die vorherige Struktur werden hier die Eingabedaten auf dem Hilfs-Qubit codiert und dann das Codierungsgatter mithilfe datenunabhängiger Operationen auf dem Arbeits-Qubit implementiert. Der Unterschied besteht darin, Gate-Teleportation, eine Art messungsbasiertes Quantencomputing, zu verwenden, um Codierungs-Gates direkt auf den Hilfs-Qubits zu implementieren und sie bei Bedarf (über Verschränkungsmessungen) zurück zu den Arbeits-Qubits zu teleportieren.
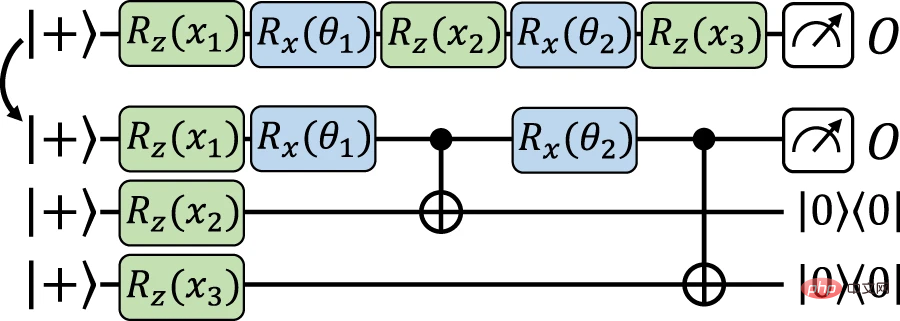
Abbildung 4: Exakte Zuordnung vom Daten-Reupload-Modell zum äquivalenten expliziten Modell unter Verwendung von Gated-Teleportation. (Quelle: Papier)
Forscher haben gezeigt, dass lineare Quantenmodelle nicht nur explizite und implizite Modelle, sondern auch Daten-Re-Upload-Schaltkreise beschreiben können. Genauer gesagt kann jede Hypothesenklasse von Modellen zum erneuten Hochladen von Daten einer äquivalenten Klasse expliziter Modelle zugeordnet werden, d. h. linearen Modellen mit einer eingeschränkten Familie von Observablen.
Als nächstes analysierten die Forscher die Vorteile expliziter Modelle und Modelle zum erneuten Hochladen von Daten gegenüber impliziten Modellen genauer. Im Beispiel wird die Effizienz des Quantenmodells bei der Lösung der Lernaufgabe durch die Anzahl der Qubits und die Größe des Trainingssatzes quantifiziert, die erforderlich sind, um einen nicht trivialen erwarteten Verlust zu erreichen. Die interessante Lernaufgabe besteht darin, ungerade und gerade Funktionen zu lernen.
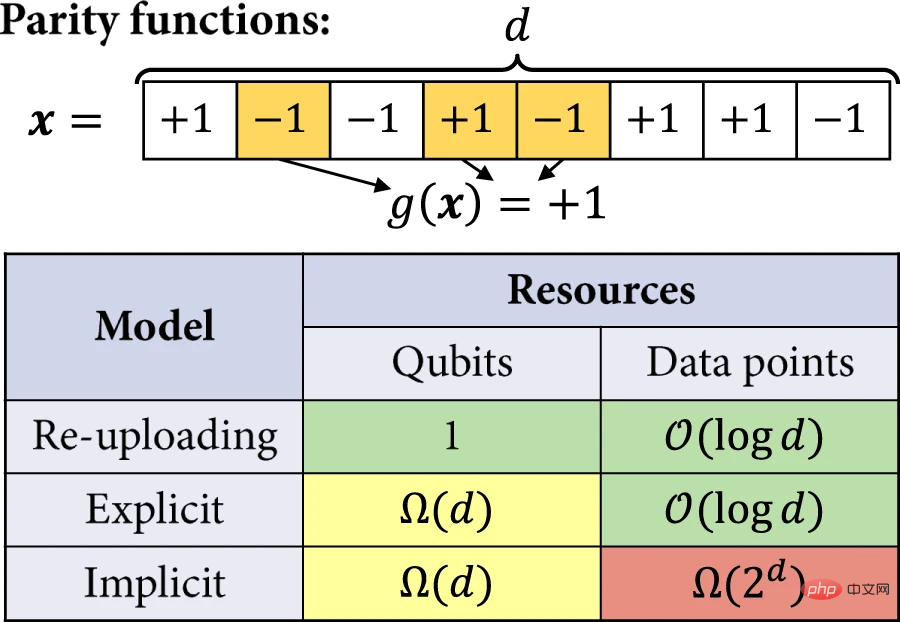
Abbildung 5: Trennen lernen. (Quelle: Paper)
Quantum Advantages Beyond Kernel Methods
Eine große Herausforderung beim Quantenmaschinellen Lernen besteht darin zu zeigen, dass die in dieser Arbeit diskutierten Quantenmethoden Lernvorteile gegenüber (Standard-)klassischen Methoden erzielen können.
In dieser Studie haben Huang et al. von Google Quantum Artificial Intelligence (https://www.php.cn/link/4dfd2a142d36707f8043c40ce0746761 ) Es empfiehlt sich, Lernaufgaben zu studieren, bei denen die Zielfunktion selbst durch (explizite) Quantenmodelle erzeugt wird.
Ähnlich wie Huang et al. führten die Forscher die Regressionsaufgabe mithilfe von Eingabedaten aus dem Fashion-MNIST-Datensatz durch, wobei jedes Beispiel ein 28x28-Graustufenbild war.
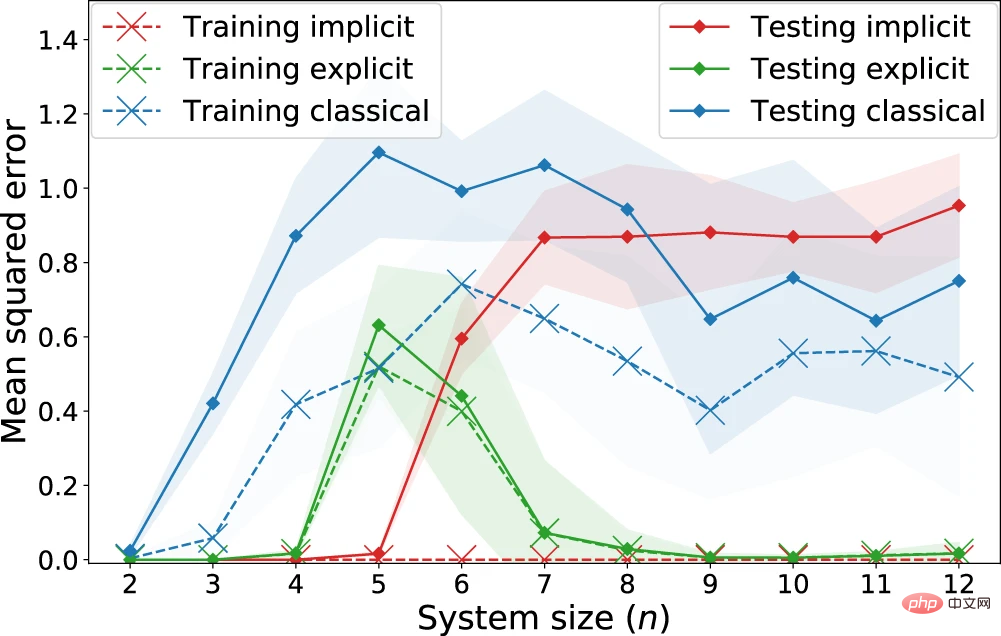
Abbildung 6: Regressionsleistung expliziter, impliziter und klassischer Modelle zur Lernaufgabe „Quantenanpassung“. (Quelle: Paper)
Beobachtet: Implizite Modelle erzielen systematisch geringere Trainingsverluste als explizite Modelle. Insbesondere für nicht regulierte Verluste erreicht das implizite Modell einen Trainingsverlust von 0. Bezüglich der Testverluste, die die erwarteten Verluste darstellen, gibt es hingegen ab n = 7 Qubits eine klare Trennung, bei der das klassische Modell beginnt, mit dem impliziten Modell konkurrenzfähig zu sein, während das explizite Modell beide deutlich übertrifft . Dies legt nahe, dass das Vorhandensein eines Quantenvorteils nicht allein durch den Vergleich klassischer Modelle mit Quantenkernmethoden beurteilt werden sollte, da explizite Modelle (oder Modelle mit erneutem Hochladen von Daten) auch eine bessere Lernleistung verbergen können.
Diese Ergebnisse geben uns ein umfassenderes Verständnis des Bereichs des Quantenmaschinellen Lernens und erweitern unseren Blick auf die Modelltypen, um praktische Lernvorteile in NISQ-Mechanismen zu erzielen.
Die Forscher glauben, dass die Lernaufgabe, die Existenz einer exponentiellen Lerntrennung zwischen verschiedenen Quantenmodellen zu beweisen, auf ungeraden und geraden Funktionen basiert, was keine konzeptionelle Klasse von praktischem Interesse für maschinelles Lernen darstellt. Die Ergebnisse der Untergrenze können jedoch auch auf andere Lernaufgaben mit großdimensionalen Konzeptklassen (d. h. bestehend aus vielen orthogonalen Funktionen) erweitert werden.
Quantum-Kernel-Methoden erfordern notwendigerweise viele Datenpunkte, die linear mit dieser Dimension skalieren, und wie wir in unseren Ergebnissen zeigen, sparen die Flexibilität von Daten-Re-Upload-Schaltkreisen und die begrenzten Ausdrucksmöglichkeiten expliziter Modelle erhebliche Ressourcen. Die Untersuchung, wie und wann diese Modelle auf die jeweilige maschinelle Lernaufgabe zugeschnitten werden können, bleibt eine interessante Forschungsrichtung.
Das obige ist der detaillierte Inhalt vonQuantenmaschinelles Lernen über Kernel-Methoden hinaus, ein einheitliches Framework für Quantenlernmodelle. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

