NP hat die Schafe völlig geknackt und ein Schaf verloren?

In letzter Zeit ist Yang Liao Ge Yang im Internet populär geworden. Es gibt mehr Artikel darüber, wie schwierig das zweite Level ist und wie man es besteht. Es sollte jedoch keine Artikel geben, die den Schwierigkeitsgrad des Spiels aus der Perspektive von Daher habe ich dieses Mal auch einen Artikel über die Komplexität der Berechnungen geschrieben, um einige Ideen zu sammeln.

Der Spielmechanismus ist relativ einfach, es gibt verschiedene Arten von Blöcken auf der Karte (die Slots haben eine Konstante). Der Slot besteht darin, drei Blöcke des gleichen Typs zu eliminieren. Das Ziel des Spiels ist es, alle Blöcke zu eliminieren. Die Schwierigkeit des Spiels besteht darin, dass die unten gestapelten Blöcke nicht ausgewählt (d. h. freigeschaltet) werden können, nachdem die Blöcke oben in die Steckplätze gelegt wurden Die Typen sind unbekannt, da sie unklar sind.

Tatsächlich ist der Mechanismus von Sheep of Sheep dem einiger Minispiele sehr ähnlich, und viele dieser Minispiele haben sich als NP-vollständig erwiesen, sodass wir relativ zuversichtlich sind, dass wir dies auch beweisen können dass das geförderte Schaf von Schafen NP-vollständig ist. Hier geben wir eine relativ schwache und einfache Reduktionsstruktur an, um zu veranschaulichen, dass das geförderte Schaf-zu-Schaf-Spiel NP-vollständig ist. Die Verallgemeinerung, über die wir hier sprechen, bedeutet, dass die Anzahl der Blocktypen nicht auf eine Konstante beschränkt ist, der blockierte Blocktyp bestimmt und bekannt ist und die Anzahl der Slots auf 3 festgelegt ist (eine ähnliche Methode kann verwendet werden, wenn die Anzahl der Slots sind andere Konstanten, solange der Spieler zu Beginn des Spiels gezwungen ist, einen speziellen Blocktyp zu nehmen, der erst am Ende des Spiels entfernt werden kann. Während des gesamten Prozesses belegt dieser Block einen Slot. was dem Fehlen eines Steckplatzes gleichkommt). Natürlich berücksichtigen wir hier nicht die Auswirkungen von Spiel-Requisiten.

Die Reduzierung in diesem Artikel ist hauptsächlich ein Plagiat der Webseite Computational Complexity of Games and Puzzles, die beweist, dass das Mah-Jongg-Spiel (ein Spiel ähnlich Lianliankan, an manchen Stellen auch Mahjong genannt) NP-vollständig ist.

Als Reduktionsproblem verwenden wir immer noch das klassische NP-vollständige Problem von 3-SAT. Wir richten für jede Variable in der 3-SAT-Formel drei quadratische Stapel ein. Ein quadratischer Stapel wird verwendet, um die Zuweisung der Variablen (WAHR oder FALSCH) zu simulieren, ein quadratischer Stapel entspricht der Zuweisung von FALSCH und ein Stapel entspricht der Zuweisung Zuweisung von TRUE. Der Stapel der Zuweisungsblöcke für simulierte Variablen besteht aus zwei Ebenen. Die erste Ebene enthält 4 identische Blöcke, die den Variablen entsprechen. Die zweite Ebene enthält jeweils einen Block mit den Variablen TRUE und FALSE sowie einen Füllblock. Der Heap von Blöcken, der dem FALSE-Wert zugewiesen ist, ist normalerweise mehrschichtig (kann auch auf eine Ebene reduziert werden). Die oberste Ebene enthält zwei Blöcke, die der FALSE-Variablen entsprechen (zur Verwendung mit dem zuvor zugewiesenen Block-Heap). und die untere Ebene enthält die Blöcke, die der Variablen entsprechen, die FALSE zugewiesen ist (entsprechend Klauseln, in denen Variablen als nicht angezeigt werden) und Füllquadrate. Die Struktur, die dem mit TRUE zugewiesenen Blockheap entspricht, ist ähnlich. Schließlich gibt es einen Stapel von Quadraten, der zur Überprüfung der Lösung verwendet wird. Dieser Stapel ist eine mehrschichtige Struktur. Die Oberseite enthält Quadrate, die den Klauseln entsprechen, die Mitte sind Quadrate, die den Klauseln entsprechen.

Wir verwenden ein konkretes Beispiel, um diese Reduzierung zu beschreiben, wobei wir davon ausgehen, dass die Instanz von 3-SAT 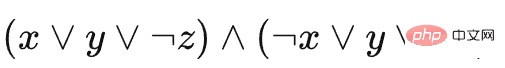ist. Dann sieht das Beispiel des Schafe-ein-Schafe-Spiels wie folgt aus (um den Typ und die Stapelsituation jedes Blocks auszudrücken, verwenden wir die Seitenansicht zur Anzeige)

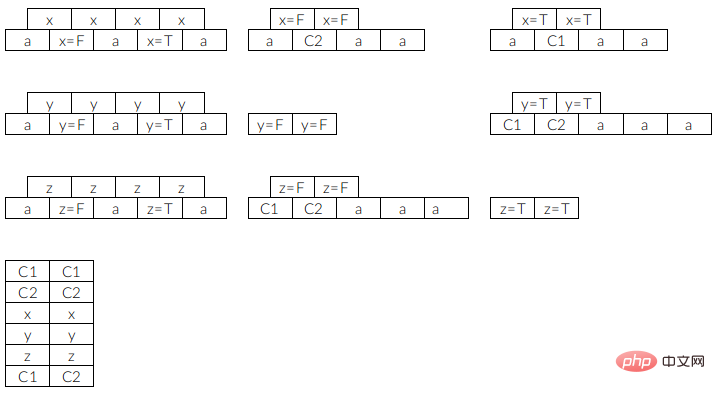
wobei C1 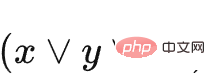darstellt und C2 stellt 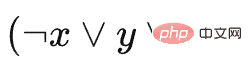dar, a ist ein Füllblock und Block a unterdrückt keine Blöcke, sodass er bis zum Ende belassen und dann alle entfernt werden kann, ohne dass sich dies auf andere Blöcke auswirkt. Beachten Sie, dass die Anzahl der Slots, die wir hier festlegen, 3 beträgt. Das bedeutet, dass Sie diesen Blocktyp entfernen müssen, nachdem Sie einen bestimmten Block ausgewählt und in den Slot platziert haben, andernfalls wird das Spiel nicht fortgesetzt.

Wenn die Formel erfüllt werden kann, können die Blöcke entsprechend der Zuweisung jeder Variablen eliminiert werden, wenn sie erfüllt ist. Nehmen wir beispielsweise an, dass xyz alle als FALSE zugewiesen sind, dann eliminieren wir die drei am weitesten links stehenden x, y und z. Auf diese Weise werden die Quadrate der zweiten Ebene x=F, y=F und z=F entsperrt. und wir können sie alle x=F y=F z=F Blöcke eliminieren, dann werden ein C1-Block und zwei C2-Blöcke entsperrt, und dann können mit dem unteren Verifizierungsblockstapel die oberen beiden Schichten des Verifizierungsstapels eliminiert werden , und dann wird auch der mittlere variable xyz-Block entsperrt. Er kann sofort entfernt werden, und am Ende gibt es keine Begrenzung, alle Blöcke können entfernt werden.

Umgekehrt kann die Formel erfüllt werden, wenn alle Blöcke beseitigt werden können (das heißt, das Level kann gelöscht werden). Beachten Sie, dass, wenn der variable xyz-Block im Überprüfungsheap entfernt werden soll, zuerst die oberen C1-C2-Klauselblöcke entfernt werden müssen und der Klauselblock auf den Zuweisungsblock beschränkt ist, der Zuweisungsblock auf den Variablenblock beschränkt ist Platzierung des Variablenblocks Die Platzierungsmethode legt fest, dass beim Zuweisen von Werten zu Variablen jede Variable nur entweder FALSCH oder WAHR zugewiesen werden kann (insbesondere nach willkürlicher Eliminierung von 3 der 4 x-Quadrate zu Beginn des Spiels). Quadrate x=F und x=T Es muss eines geben, das nicht freigeschaltet ist). Dies bedeutet, dass die Reihenfolge, in der die Blöcke entfernt werden, eine Zuordnung impliziert, die der Formel entspricht.

Dies bedeutet, dass die notwendige und ausreichende Bedingung, die die 3-SAT-Formel erfüllen kann, darin besteht, dass die entsprechende Sheep of Sheep-Spielinstanz bestanden werden kann. Und Sheep Got a Sheep gehört offensichtlich zu NP, da in polynomialer Zeit bestimmt werden kann, ob eine Operationssequenz alle Blöcke eliminieren kann. Daher haben wir den folgenden Satz bewiesen:

#🎜🎜 # Vorschlag: Unter der Bedingung, dass die Typen aller okkludierten Blöcke bestimmt und bekannt sind, ist das geförderte Schaf-gegen-Schaf-Spiel NP-vollständig.

In nicht-menschlichen Begriffen haben Sie keine Möglichkeit, einen polynomialen Zeitkomplexitätsalgorithmus zu entwerfen, um zu bestimmen, ob eine geförderte Schafebene eine Lösung hat, es sei denn, P=NP (Dies Eine 4-stellige Gleichung ist einen Landpreis und 1 Million US-Dollar wert, also machen Sie sich nicht die Mühe, sie zu beweisen oder zu widerlegen. Menschlich gesehen ist der Computer, selbst wenn die Art des blockierten Blocks sicher und bekannt ist, immer noch (fast) nicht in der Lage, schnell zu bestimmen, ob ein Schaf das Level bestehen kann.

Das obige ist der detaillierte Inhalt vonNP hat die Schafe völlig geknackt und ein Schaf verloren?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!