Heim >Technologie-Peripheriegeräte >KI >Anatomie des Entscheidungsbaumalgorithmus
Anatomie des Entscheidungsbaumalgorithmus
- 王林nach vorne
- 2023-04-12 22:01:051909Durchsuche
Übersetzer |. Rezensiert von Zhao Qingyu
Vorwort
Beim maschinellen Lernen gibt es zwei Phasen, nämlich die Lernphase und die Vorhersagephase. In der Lernphase wird ein Modell basierend auf den gegebenen Trainingsdaten erstellt; in der Vorhersagephase wird das Modell verwendet, um die Reaktion anhand der Daten vorherzusagen. Entscheidungsbäume sind einer der am einfachsten zu verstehenden und zu erklärenden Klassifizierungsalgorithmen.Beim maschinellen Lernen besteht die Klassifizierung aus zwei Phasen, nämlich der Lernphase und der Vorhersagephase. In der Lernphase wird ein Modell basierend auf den gegebenen Trainingsdaten erstellt; in der Vorhersagephase wird das Modell verwendet, um die Reaktion anhand der Daten vorherzusagen. Entscheidungsbäume sind einer der am einfachsten zu verstehenden und zu erklärenden Klassifizierungsalgorithmen.
Entscheidungsbaumalgorithmus
Der Entscheidungsbaumalgorithmus ist eine Art überwachter Lernalgorithmus. Im Gegensatz zu anderen überwachten Lernalgorithmen kann der Entscheidungsbaumalgorithmus sowohl zur Lösung von Regressions- als auch von Klassifizierungsproblemen verwendet werden.
Der Zweck der Verwendung von Entscheidungsbäumen besteht darin, ein Trainingsmodell zu erstellen, das die Klasse oder den Wert einer Zielvariablen vorhersagt, indem es einfache Entscheidungsregeln lernt, die aus vorherigen Daten (Trainingsdaten) abgeleitet werden.
In Entscheidungsbäumen beginnen wir an der Wurzel des Baums, um die Klassenbezeichnung eines Datensatzes vorherzusagen. Wir vergleichen den Wert des Stammattributs mit dem aufgezeichneten Attribut und folgen basierend auf dem Vergleich dem diesem Wert entsprechenden Zweig und springen zum nächsten Knoten.
Arten von Entscheidungsbäumen
Basierend auf der Art der Zielvariablen, die wir haben, können wir den Baum in zwei Typen unterteilen:
1. Entscheidungsbaum mit kategorialer Variable: Ein Entscheidungsbaum mit einer kategorialen Zielvariablen wird als kategoriale Variable Entscheidung bezeichnet Baum.
2. Entscheidungsbaum mit kontinuierlichen Variablen: Die Zielvariable des Entscheidungsbaums ist kontinuierlich und wird daher als Entscheidungsbaum mit kontinuierlichen Variablen bezeichnet.
Beispiel: Angenommen, wir haben ein Problem bei der Vorhersage, ob ein Kunde eine Verlängerungsprämie an eine Versicherungsgesellschaft zahlen wird. Das Einkommen eines Kunden ist hier eine wichtige Variable, aber Versicherungsunternehmen verfügen nicht über Einkommensdetails für alle Kunden. Da wir nun wissen, dass dies eine wichtige Variable ist, können wir einen Entscheidungsbaum erstellen, um den Umsatz eines Kunden basierend auf Beruf, Produkt und verschiedenen anderen Variablen vorherzusagen. In diesem Fall sagen wir voraus, dass die Zielvariable kontinuierlich ist.
Wichtige Begriffe im Zusammenhang mit Entscheidungsbäumen
1 Wurzelknoten: Er stellt das gesamte Mitglied oder die gesamte Stichprobe dar, die weiter in zwei oder mehr Sätze desselben Typs unterteilt wird.
2. Aufteilung): Der Vorgang der Aufteilung eines Knotens in zwei oder mehr untergeordnete Knoten.
3. Entscheidungsknoten: Wenn sich ein untergeordneter Knoten in weitere untergeordnete Knoten aufteilt, wird er als Entscheidungsknoten bezeichnet.
4. Blatt-/Endknoten: Ein Knoten, der nicht geteilt werden kann, wird als Blatt- oder Endknoten bezeichnet.
5. Beschneiden: Der Vorgang, bei dem wir die untergeordneten Knoten eines Entscheidungsknotens löschen, wird als Beschneiden bezeichnet. Bauen kann auch als umgekehrter Prozess der Trennung betrachtet werden.
6. Zweig/Unterbaum: Ein Unterteil des gesamten Baums wird als Zweig oder Unterbaum bezeichnet.
7. Übergeordneter und untergeordneter Knoten: Ein Knoten, der in untergeordnete Knoten aufgeteilt werden kann, wird als übergeordneter Knoten bezeichnet, und ein untergeordneter Knoten ist ein untergeordneter Knoten des übergeordneten Knotens.
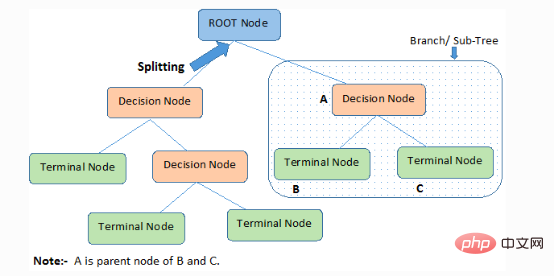 Der Entscheidungsbaum klassifiziert Proben in absteigender Reihenfolge von der Wurzel bis zu den Blatt-/Endknoten, die die Klassifizierungsmethode der Probe bereitstellen. Jeder Knoten im Baum fungiert als Testfall für ein bestimmtes Attribut, und jede absteigende Richtung vom Knoten entspricht einer möglichen Antwort auf den Testfall. Dieser Prozess ist rekursiver Natur und wird für jeden Teilbaum, der an einem neuen Knoten verwurzelt ist, gleich behandelt.
Der Entscheidungsbaum klassifiziert Proben in absteigender Reihenfolge von der Wurzel bis zu den Blatt-/Endknoten, die die Klassifizierungsmethode der Probe bereitstellen. Jeder Knoten im Baum fungiert als Testfall für ein bestimmtes Attribut, und jede absteigende Richtung vom Knoten entspricht einer möglichen Antwort auf den Testfall. Dieser Prozess ist rekursiver Natur und wird für jeden Teilbaum, der an einem neuen Knoten verwurzelt ist, gleich behandelt.
Annahmen bei der Erstellung von Entscheidungsbäumen
Hier sind einige Annahmen, die wir bei der Verwendung von Entscheidungsbäumen treffen:
●Nehmen Sie zunächst den gesamten Trainingssatz als Wurzel.
●Merkmalswerte werden am besten klassifiziert. Wenn diese Werte kontinuierlich sind, können sie vor der Erstellung des Modells diskretisiert werden.
●Datensätze werden basierend auf Attributwerten rekursiv verteilt.
●Durch die Verwendung einiger statistischer Methoden, um die entsprechenden Attribute am Wurzelknoten des Baums oder an den internen Knoten des Baums in die richtige Reihenfolge zu bringen.
Entscheidungsbäume folgen der Ausdrucksform „Summe der Produkte“. Die Summe der Produkte (SOP) wird auch als disjunktive Normalform bezeichnet. Für eine Klasse ist jeder Zweig von der Wurzel des Baums zu einem Blattknoten derselben Klasse eine Konjunktion von Werten, und die verschiedenen Zweige, die in der Klasse enden, bilden eine Disjunktion.
Die größte Herausforderung im Implementierungsprozess des Entscheidungsbaums besteht darin, die Attribute des Wurzelknotens und jedes Ebenenknotens zu bestimmen. Dieses Problem ist das Attributauswahlproblem. Derzeit gibt es verschiedene Attributauswahlmethoden, um die Attribute von Knoten auf jeder Ebene auszuwählen.
Wie funktionieren Entscheidungsbäume?
Die Trennungsmerkmale der Entscheidungsfindung wirken sich stark auf die Genauigkeit des Baums aus. Die Entscheidungskriterien von Klassifizierungsbäumen und Regressionsbäumen sind unterschiedlich.
Entscheidungsbäume verwenden eine Vielzahl von Algorithmen, um zu entscheiden, ob ein Knoten in zwei oder mehr untergeordnete Knoten aufgeteilt werden soll. Durch die Erstellung von untergeordneten Knoten wird die Homogenität der untergeordneten Knoten erhöht. Mit anderen Worten: Die Reinheit des Knotens wird im Verhältnis zur Zielvariablen erhöht. Der Entscheidungsbaum trennt Knoten nach allen verfügbaren Variablen und wählt dann Knoten aus, die viele isomorphe untergeordnete Knoten zur Aufteilung erzeugen können.
Der Algorithmus wird basierend auf der Art der Zielvariablen ausgewählt. Schauen wir uns als nächstes einige Algorithmen an, die in Entscheidungsbäumen verwendet werden:
ID3→(Erweiterung von D3)
C4.5→(Nachfolger von ID3)
CART→(Klassifizierungs- und Regressionsbaum)
CHAID→ (Chi
MARS→ (Multiple Adaptive Regression Splines)
Der ID3-Algorithmus verwendet gierige Suchmethoden von oben nach unten, die Entscheidungsbäume durch den Raum möglicher Zweige ohne Backtracking erstellen. Gierige Algorithmen treffen, wie der Name schon sagt, immer die Wahl, die zu einem bestimmten Zeitpunkt die beste zu sein scheint.
ID3-Algorithmusschritte:
1. Es wird der ursprüngliche Satz S als Wurzelknoten verwendet.
2. Iterieren Sie bei jeder Iteration des Algorithmus über die nicht verwendeten Attribute in der Menge S und berechnen Sie die Entropie (H) und den Informationsgewinn (IG) des Attributs.
3. Wählen Sie dann das Attribut mit der kleinsten Entropie oder dem größten Informationsgewinn aus.
4. Trennen Sie dann die Menge S mithilfe der ausgewählten Attribute, um Teilmengen der Daten zu generieren.
5. Der Algorithmus iteriert weiterhin für jede Teilmenge und berücksichtigt dabei nur Attribute, die noch nie zuvor ausgewählt wurden.
Attributauswahlmethode
Wenn der Datensatz N Attribute enthält, ist die Entscheidung, welches Attribut am Wurzelknoten oder auf verschiedenen Ebenen des Baums als interner Knoten platziert werden soll, ein komplexer Schritt. Das Problem kann nicht durch die zufällige Auswahl eines beliebigen Knotens als Wurzelknoten gelöst werden. Wenn wir einen zufälligen Ansatz verfolgen, erhalten wir möglicherweise schlechtere Ergebnisse.
Um dieses Problem der Attributauswahl zu lösen, haben Forscher einige Lösungen entwickelt. Sie schlagen die Verwendung der folgenden Kriterien vor:
- Entropie
- Informationsgewinn
- Gini-Index
- Gewinnrate
- Varianzreduktion
- Chi-Quadrat
Berechnen Sie den Wert jedes Attributs anhand dieser Kriterien und ordnen Sie diese Werte dann in eine Rangfolge. Und die Attribute werden der Reihe nach im Baum platziert, das heißt, die Attribute mit hohen Werten werden an der Stammposition platziert.
Wenn wir den Informationsgewinn als Kriterium verwenden, gehen wir davon aus, dass die Attribute kategorisch sind, während wir für den Gini-Index davon ausgehen, dass die Attribute kontinuierlich sind.
1. Entropie
Entropie ist ein Maß für die Zufälligkeit der verarbeiteten Informationen. Je höher der Entropiewert, desto schwieriger ist es, aus den Informationen Rückschlüsse zu ziehen. Das Werfen einer Münze ist ein Beispiel für ein Verhalten, das zufällige Informationen liefert.
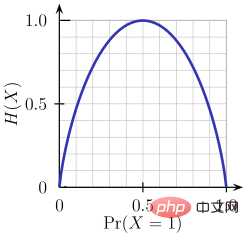
Wie aus der obigen Abbildung ersichtlich ist, ist die Entropie H(X) Null, wenn die Wahrscheinlichkeit 0 oder 1 ist. Die Entropie ist am größten, wenn die Wahrscheinlichkeit 0,5 beträgt, da sie eine vollständige Zufälligkeit der Daten projiziert.
Die von ID3 befolgte Regel lautet: Ein Zweig mit einer Entropie von 0 ist ein Blattknoten, und ein Zweig mit einer Entropie größer als 0 muss weiter getrennt werden.
Die mathematische Entropie eines einzelnen Attributs wird wie folgt ausgedrückt:

wobei S den aktuellen Zustand darstellt und Pi die Wahrscheinlichkeit des Ereignisses i im Zustand S oder den Prozentsatz der Klasse i in den Knoten des Zustands S darstellt.
Die mathematische Entropie mehrerer Attribute wird wie folgt ausgedrückt:
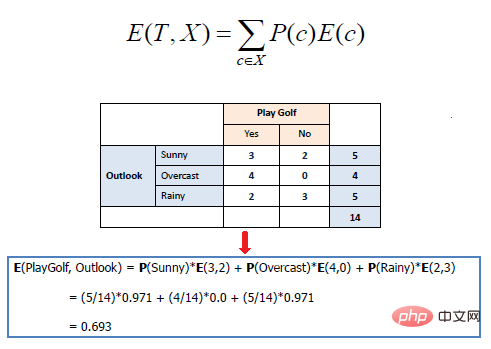
wobei T den aktuellen Zustand darstellt und den Effekt eines separaten Trainings für ein bestimmtes Attribut entsprechend der Zielklasse misst. Beim Erstellen eines Entscheidungsbaums geht es darum, ein Attribut zu finden, das den höchsten Informationsgewinn und die niedrigste Entropie zurückgibt.
Die Zunahme der Information ist die Abnahme der Entropie. Es berechnet die Entropiedifferenz vor der Trennung des Datensatzes und die durchschnittliche Entropiedifferenz nach der Trennung basierend auf den angegebenen Attributwerten. Der ID3-Entscheidungsbaumalgorithmus verwendet die Informationsgewinnmethode.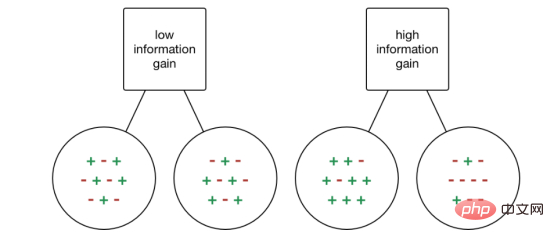 IG wird mathematisch wie folgt ausgedrückt:
IG wird mathematisch wie folgt ausgedrückt:

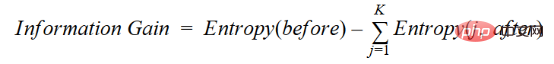 3. Gini-Index
3. Gini-Index
Sie können den Gini-Index als eine Kostenfunktion verstehen, die zur Bewertung der Trennung in einem Datensatz verwendet wird. Sie wird berechnet, indem die Summe der quadrierten Wahrscheinlichkeiten für jede Klasse von 1 subtrahiert wird. Dies begünstigt den Fall größerer Partitionen und ist einfacher zu implementieren, während der Informationsgewinn den Fall kleinerer Partitionen mit unterschiedlichen Werten begünstigt.
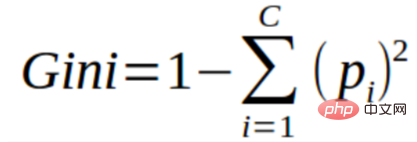
Der Gini-Index ist untrennbar mit der kategorialen Zielvariablen „Erfolg“ oder „Misserfolg“ verbunden. Es führt nur eine binäre Trennung durch. Je höher der Gini-Koeffizient, desto höher der Grad der Ungleichheit und desto stärker die Heterogenität.
Die Schritte zur Berechnung der Gini-Index-Trennung lauten wie folgt:
- Berechnen Sie den Gini-Koeffizienten des untergeordneten Knotens unter Verwendung der obigen Formel (p²+q²) für Erfolg (p) und Misserfolg (q).
- Berechnen Sie den Gini-Koeffizientenindex der Trennung anhand des gewichteten Gini-Scores jedes Knotens der Trennung.
CART (Classification and Regression Tree) verwendet die Gini-Indexmethode, um Trennpunkte zu erstellen.
4. Gewinnrate
Der Informationsgewinn wählt tendenziell Attribute mit einer großen Anzahl von Werten als Wurzelknoten aus. Das bedeutet, dass Eigenschaften mit einer großen Anzahl unterschiedlicher Werte bevorzugt werden.
C4.5 ist eine verbesserte Methode von ID3. Sie verwendet das Verstärkungsverhältnis, eine Modifikation des Informationsgewinns, um dessen Verzerrung zu verringern. Dies ist normalerweise die Methode der besten Wahl. Die Verstärkungsrate überwindet das Problem des Informationsgewinns, indem sie vor der Aufteilung die Anzahl der Zweige berücksichtigt. Es korrigiert den Informationsgewinn, indem es separate intrinsische Informationen berücksichtigt.
Angenommen, wir haben einen Datensatz, der Benutzer und ihre Vorlieben für Filmgenres basierend auf Variablen wie Geschlecht, Altersgruppe, Klasse usw. enthält. Mit Hilfe des Informationsgewinns trennen Sie nach „Geschlecht“ (vorausgesetzt, es hat den höchsten Informationsgewinn). Jetzt können die Variablen „Altersgruppe“ und „Bewertung“ gleich wichtig sein. Mithilfe des Gewinnverhältnisses können wir Eigenschaften auswählen, die werden in der nächsten Schicht getrennt.
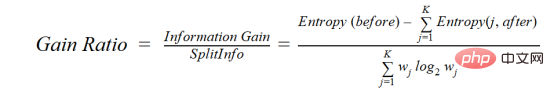
wobei before der Datensatz vor der Trennung ist, K die Anzahl der durch die Trennung erzeugten Teilmengen ist und (j, after) die Teilmenge j nach der Trennung ist.
5. Varianzreduktion
Varianzreduktion ist ein Algorithmus, der für kontinuierliche Zielvariablen (Regressionsprobleme) verwendet wird. Der Algorithmus verwendet die Standardvarianzformel, um die beste Trennung auszuwählen. Wählen Sie die Trennung mit geringerer Varianz als Kriterium für die Trennung der Grundgesamtheit:
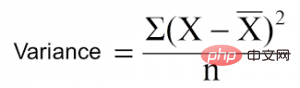
ist der Mittelwert, X ist der tatsächliche Wert und n ist die Anzahl der Werte.
Schritte zur Berechnung der Varianz:
- Berechnen Sie die Varianz jedes Knotens.
- Berechnen Sie die Varianz jeder Trennung und verwenden Sie sie als gewichteten Durchschnitt der Varianz jedes Knotens.
6. Chi-Quadrat
CHAID ist die Abkürzung für Chi-Quadrat-Automatischer Interaktionsdetektor. Dies ist eine der älteren Baumklassifizierungsmethoden. Finden Sie den statistisch signifikanten Unterschied zwischen einem untergeordneten Knoten und seinem übergeordneten Knoten. Wir messen es anhand der Summe der quadrierten Differenzen zwischen den beobachteten und erwarteten Häufigkeiten der Zielvariablen.
Es funktioniert mit der kategorialen Zielvariablen „Erfolg“ oder „Misserfolg“. Es können zwei oder mehr Trennungen durchgeführt werden. Je höher der Chi-Quadrat-Wert, desto statistisch signifikanter ist der Unterschied zwischen dem untergeordneten Knoten und dem übergeordneten Knoten. Es generiert einen Baum namens CHAID.
Mathematisch wird das Chi-Quadrat wie folgt ausgedrückt:

Die Schritte zur Berechnung des Chi-Quadrats sind wie folgt:
- Berechnen Sie das Chi-Quadrat eines einzelnen Knotens, indem Sie die Abweichung von berechnen Erfolg und Misserfolg
- Berechnen Sie das getrennte Chi-Quadrat anhand der Summe aller Chi-Quadrate für Erfolg und Misserfolg jedes einzelnen Knotens
Wie vermeidet bzw. bekämpft man eine Überanpassung von Entscheidungsbäumen?
Es gibt eine Ein häufiges Problem bei Entscheidungsbäumen besteht insbesondere bei einem Baum voller Spalten. Manchmal sieht es so aus, als hätte der Baum den Trainingsdatensatz gespeichert. Wenn ein Entscheidungsbaum keine Einschränkungen hätte, würde er eine 100-prozentige Genauigkeit des Trainingsdatensatzes liefern, da er im schlimmsten Fall für jede Beobachtung ein Blatt erzeugen würde. Dies wirkt sich daher auf die Genauigkeit bei der Vorhersage von Stichproben aus, die nicht Teil des Trainingssatzes sind.
Hier stelle ich zwei Methoden zur Beseitigung von Überanpassungen vor, nämlich das Beschneiden von Entscheidungsbäumen und zufälligen Wäldern.
1. Entscheidungsbaum beschneiden
分 Durch den Aus-Prozess entsteht ein ausgewachsener Baum, bis das Stoppkriterium erreicht ist. Bei ausgewachsenen Bäumen ist es jedoch wahrscheinlich, dass sie die Daten übertreffen, was zu einer schlechten Genauigkeit bei nicht sichtbaren Daten führt.

Beim Beschneiden schneiden Sie die Zweige des Baumes ab, dh Sie löschen die Entscheidungsknoten ausgehend von den Blattknoten, um die Gesamtgenauigkeit zu gewährleisten Es wird keine Unterbrechungen geben. Dies erfolgt durch Aufteilen des eigentlichen Trainingsdatensatzes in zwei Sätze: Trainingsdatensatz D und Validierungsdatensatz V, Vorbereiten des Entscheidungsbaums mit dem getrennten Trainingsdatensatz D und anschließendes weiteres Beschneiden des Baums entsprechend, um den Validierungsdatensatz V zu optimieren Genauigkeit.
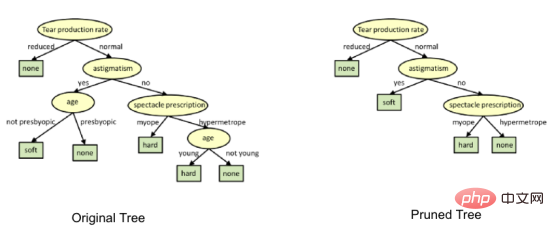
Im Bild oben wurde das Attribut „Alter“ auf der linken Seite des Baums beschnitten, da es auf der rechten Seite wichtiger ist den Baum und eliminierte daher die Überanpassung.
2. Random Forest
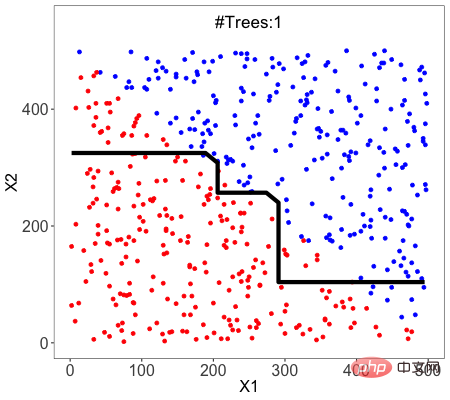
Random Forest ist ein Beispiel für Ensemble-Lernen (Ensemble Learning), um eine bessere Vorhersageleistung zu erzielen. Da der Trainingsdatensatz beim Erstellen des Baums zufällig ausgewählt wird und beim Trennen von Knoten zufällige Teilmengen von Merkmalen berücksichtigt werden, nennen wir diese Methode Zufall.
Eine Technik namens Bagging wird verwendet, um eine Sammlung von Bäumen zu erstellen, in der durch Ersetzen mehrere Trainingssätze generiert werden.
Die Bagging-Technologie verwendet Zufallsstichproben, um den Datensatz in N Stichproben aufzuteilen. Anschließend wird ein einzelner Lernalgorithmus verwendet, um das Modell für alle Stichproben zu erstellen. Die Vorhersagen werden dann durch parallele Abstimmung oder Mittelwertbildung kombiniert.
Was ist besser, ein lineares Modell oder ein baumbasiertes Modell?
Die Frage hängt von der Art des Problems ab Du versuchst es zu lösen.
1. Wenn die Beziehung zwischen der abhängigen Variablen und der unabhängigen Variablen durch ein lineares Modell gut modelliert werden kann, ist die lineare Regression besser als das baumbasierte Modell.
2. Wenn zwischen der abhängigen Variablen und der unabhängigen Variablen eine stark nichtlineare und komplexe Beziehung besteht, ist das Baummodell besser als die klassische Regressionsmethode.
3. Wenn Sie ein leicht verständliches Modell erstellen müssen, ist ein Entscheidungsbaummodell immer besser als ein lineares Modell. Entscheidungsbaummodelle sind leichter zu verstehen als lineare Regression!
Verwendung von Scikit-learn für die Konstruktion von Entscheidungsbaumklassifikatoren
Die von mir verwendeten Daten stammen von https://drive.google. com/open?id=1x1KglkvJxNn8C8kzeV96YePFnCUzXhBS hat Supermarkt-bezogene Daten heruntergeladen. Verwenden Sie zunächst den folgenden Code, um alle Basisbibliotheken zu laden:
import numpy as np import matplotlib.pyplot as plt import pandas as pd
Danach verwenden wir die Folgende Methode zum Laden des Datensatzes: Es umfasst 5 Attribute: Benutzer-ID, Geschlecht, Alter, geschätztes Gehalt und Kaufstatus.
data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()
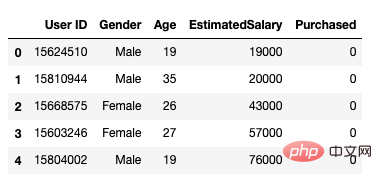
Abbildung 1 Datensatz
# 🎜 🎜#Als unabhängige Variablen verwenden wir ausschließlich das Alter und das geschätzte Gehalt
feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
Der nächste Schritt besteht darin, den Datensatz in Trainings- und Testsätze zu unterteilen.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)
Führen Sie als Nächstes die Feature-Skalierung durch 🎜 # Passen Sie das Modell in einen Entscheidungsbaumklassifikator ein.
#feature scaling from sklearn.preprocessing import StandardScaler sc_X = StandardScaler() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
Machen Sie Vorhersagen und überprüfen Sie die Genauigkeit. Der Entscheidungsbaumklassifikator hat eine Genauigkeit von 91 %.
Verwirrungsmatrixfrom sklearn.tree import DecisionTreeClassifier classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
Das bedeutet, dass 6 Beobachtungen fehlerhaft aufgeführt sind.
Lassen Sie uns zunächst die Ergebnisse der Modellvorhersage visualisieren Schauen Sie sich den Baum anAls nächstes können Sie die export_graphviz-Funktion von Scikit-learn verwenden, um den Baum in einem Jupyter-Notizbuch anzuzeigen. Um den Baum zu zeichnen, müssen wir Graphviz und pydotplus mit dem folgenden Befehl installieren:
#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))export_graphviz-Funktion konvertiert den Entscheidungsbaumklassifikator in eine Punktdatei und pydotplus Konvertiert die Punktdatei in PNG oder zeigt sie auf Jupyter an. Die spezifische Implementierungsmethode lautet wie folgt:
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)Output: array([[64,4], [ 2, 30]])
在决策树形图中,每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数,它代表了节点的纯度。当一个节点的所有记录都属于同一个类时,您可以说它是纯节点,这种节点称为叶节点。
在这里,生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中,我会通过修剪的方式来优化树。
随后优化决策树分类器
criteria: 该选项默认配置是Gini,我们可以通过该项选择合适的属性选择方法,该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。
splitter: 该选项默认配置是" best ",我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。
max_depth:默认配置是None,我们可以通过该参数设置树的最大深度。若设置为None,则节点将展开,直到所有叶子包含的样本小于min_samples_split。最大深度值越高,过拟合越严重,反之,过拟合将不严重。
在Scikit-learn中,只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。
# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
至此分类率提高到94%,相对之前的模型来说,其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。
dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
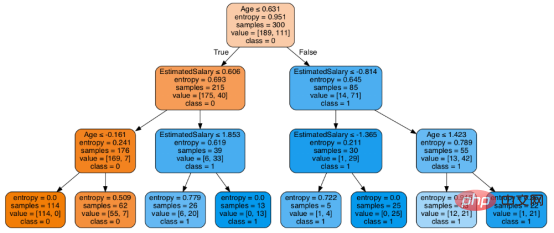
上图是经过修剪后的模型,相对之前的决策树模型图来说,其更简单、更容易解释和理解。
总结
在本文中,我们讨论了很多关于决策树的细节,它的工作方式,属性选择措施,如信息增益,增益比和基尼指数,决策树模型的建立,可视化,并使用Python Scikit-learn包评估和优化决策树性能,这就是这篇文章的全部内容,希望你们能喜欢它。
译者介绍
赵青窕,51CTO社区编辑,从事多年驱动开发。
原文标题:Decision Tree Algorithm, Explained,作者:Nagesh Singh Chauhan
Das obige ist der detaillierte Inhalt vonAnatomie des Entscheidungsbaumalgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

