Heim >Technologie-Peripheriegeräte >KI >13 Wahrscheinlichkeitsverteilungen, die beim Deep Learning beherrscht werden müssen
13 Wahrscheinlichkeitsverteilungen, die beim Deep Learning beherrscht werden müssen
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-11 21:58:121740Durchsuche
1. Überblick über die Wahrscheinlichkeitsverteilung
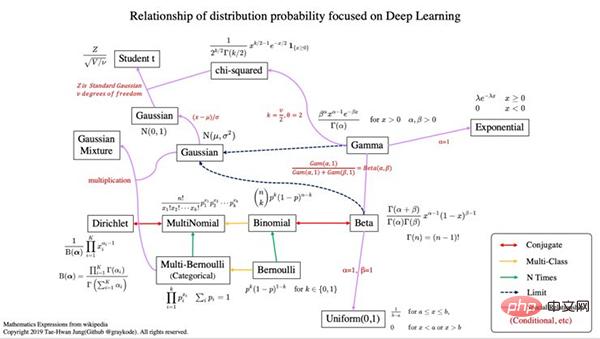
- Konjugiert bedeutet, dass es die Beziehung einer konjugierten Verteilung aufweist.
- Wenn in der Bayes'schen Wahrscheinlichkeitstheorie die Posterior-Verteilung p(θx) und die Prior-Wahrscheinlichkeitsverteilung p(θ) zur gleichen Wahrscheinlichkeitsverteilungsfamilie gehören, werden die Prior- und Posterior-Verteilung als konjugierte Verteilungen bezeichnet, und die Prior-Verteilung wird als konjugierte Prior-Verteilung bezeichnet Wahrscheinlichkeitsfunktionen. Conjugate prior Wikipedia ist hier (https://en.wikipedia.org/wiki/Conjugate_prior).
- Mehrfache Klassifizierung bedeutet, dass die Zufallsvarianz größer als 2 ist.
- n-mal bedeutet, dass wir auch die A-priori-Wahrscheinlichkeit p(x) berücksichtigen.
- Um mehr über Wahrscheinlichkeit zu erfahren, empfehle ich die Lektüre von [Mustererkennung und maschinelles Lernen, Bishop 2006].
2. Verteilungswahrscheinlichkeit und Eigenschaften
1. Gleichmäßige Verteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/uniform.py
Die Gleichverteilung hat den gleichen Wahrscheinlichkeitswert für [a, b] und ist eine einfache Wahrscheinlichkeitsverteilung.
2. Bernoulli-Verteilung (diskret)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/bernoulli.py
- Prior Die Wahrscheinlichkeit p (x) berücksichtigt nicht die Bernoulli-Verteilung. Wenn wir daher auf maximale Wahrscheinlichkeit optimieren, kann es leicht zu einer Überanpassung kommen.
- Klassifizierung mit binärer Kreuzentropie zur Binomialklassifizierung. Seine Form ist die gleiche wie der negative Logarithmus der Bernoulli-Verteilung. Bild
3. Binomialverteilung (diskret)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/binomial.py
- Die Parameter sind n und Die Binomialverteilung von p ist eine diskrete Wahrscheinlichkeitsverteilung der Anzahl der Erfolge in einer Reihe von n unabhängigen Experimenten.
- Die Binomialverteilung ist eine Verteilung, die die A-priori-Wahrscheinlichkeit berücksichtigt, indem sie die zu entnehmende Menge im Voraus angibt.
4. Multi-Bernoulli-Verteilung, kategoriale Verteilung (diskret)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/categorical.py
- Multiple Bernoulli wird als kategoriale Verteilung bezeichnet.
- Kreuzentropie hat die gleiche Form wie die Multi-Bernoulli-Verteilung unter Verwendung des negativen Logarithmus.
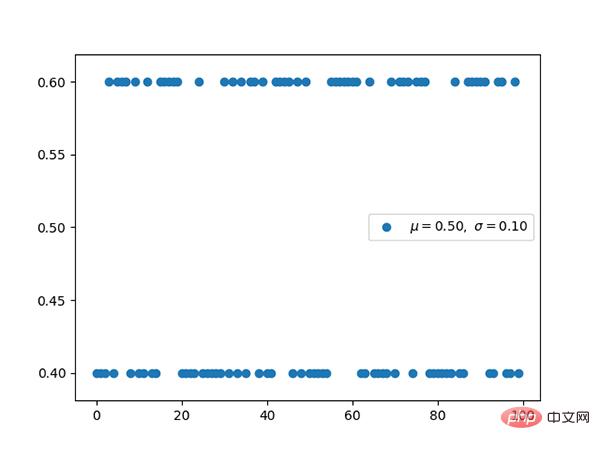
5. Polynomverteilung (diskret)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/multinomial.py
Polynomverteilung und Klassifizierung Die Beziehung zwischen den Verteilungen ist dieselbe wie die Beziehung zwischen der Bernoul-Verteilung und der Binomialverteilung.
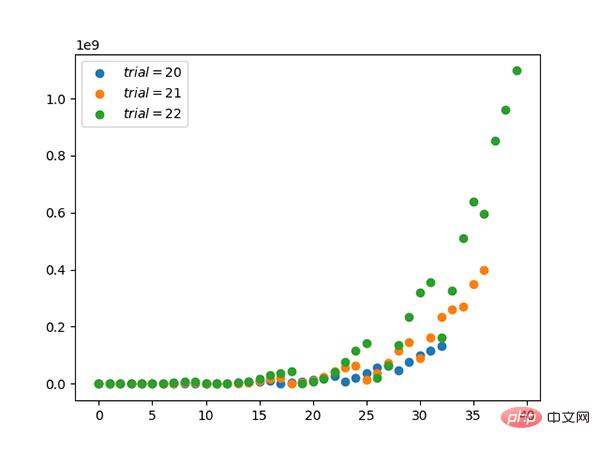
6.β-Verteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/beta.py
- β-Verteilung und zwei Der Begriff Verteilung ist mit der Bernoulli-Verteilung konjugiert.
- Durch Konjugation kann die Posterior-Verteilung einfacher mithilfe der bekannten Prior-Verteilung ermittelt werden.
- Wenn die β-Verteilung den Sonderfall (α=1, β=1) erfüllt, ist die Gleichverteilung dieselbe.
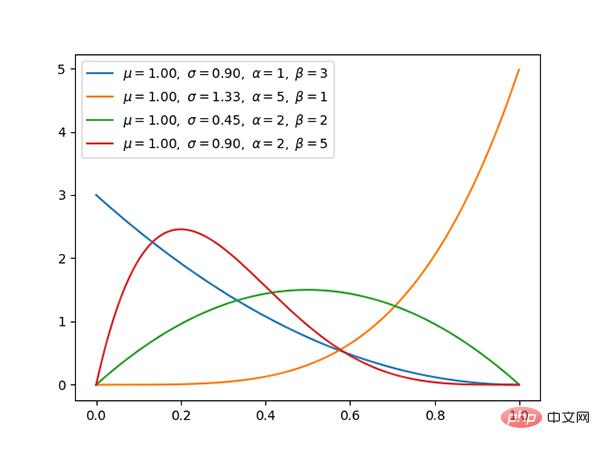
7. Dirichlet-Verteilung (fortlaufend)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/dirichlet.py
- Dirichlet-Verteilung und Polynomverteilungen sind konjugiert.
- Wenn k=2, handelt es sich um eine Beta-Verteilung.
8. Gammaverteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/gamma.py
- Wenn Gamma ( a, 1)/Gamma (a, 1) + Gamma (b, 1) ist dasselbe wie Beta (a, b), dann ist die Gammaverteilung eine Betaverteilung.
- Die Exponentialverteilung und die Chi-Quadrat-Verteilung sind Sonderfälle der Gammaverteilung.
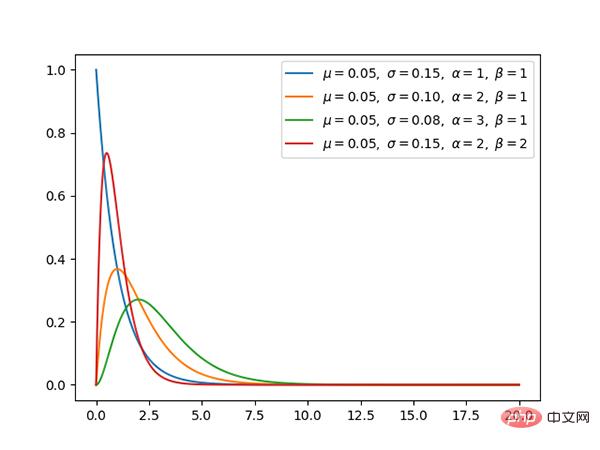
9. Exponentielle Verteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/exponential.py
Die Exponentialverteilung ist ein Sonderfall der γ-Verteilung, wenn α 1 ist.
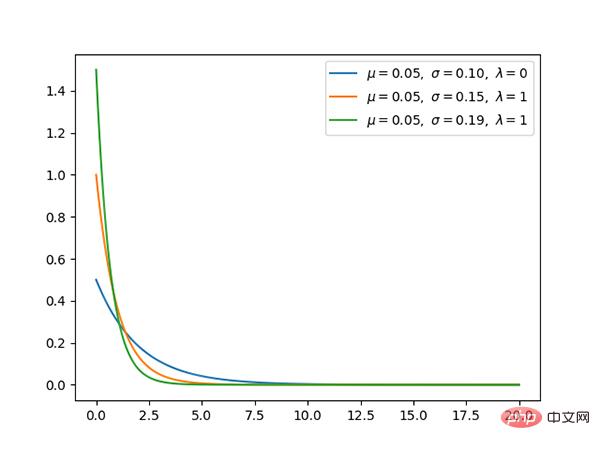
10. Gaußsche Verteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/gaussian.py
Die Gaußsche Verteilung ist eine Sehr häufige kontinuierliche Wahrscheinlichkeitsverteilung.
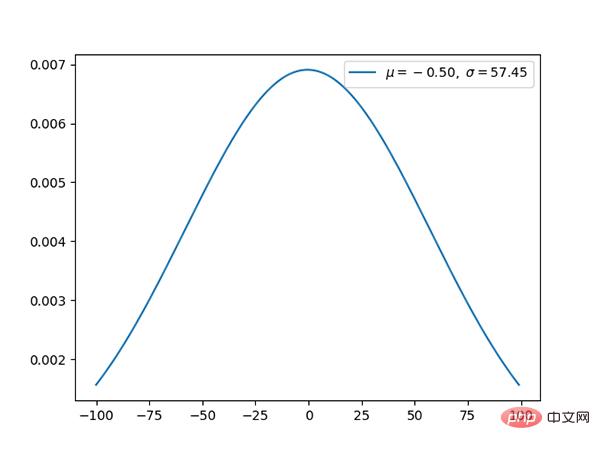
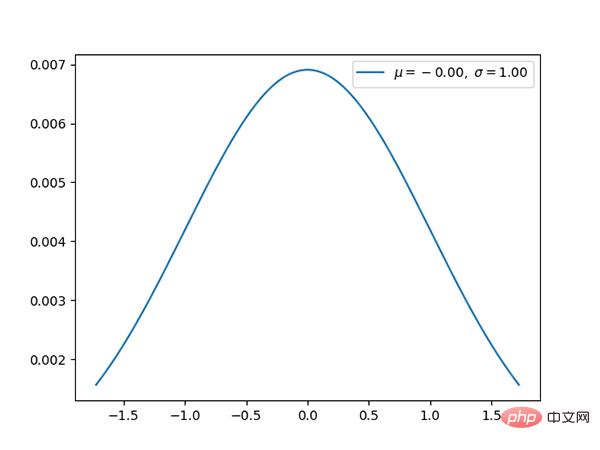
11. Normalverteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/normal.py
Die Normalverteilung ist The Die Standard-Gauß-Verteilung hat einen Mittelwert von 0 und eine Standardabweichung von 1.
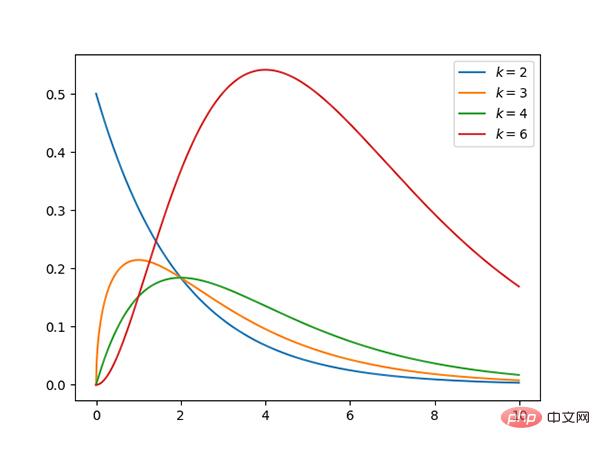
12. Chi-Quadrat-Verteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/blob/master/chi-squared.py
- k Die Chi-Quadrat-Verteilung mit Freiheitsgraden ist die Verteilung der Summe der Quadrate von k unabhängigen Standardnormal-Zufallsvariablen.
- Chi-Quadrat-Verteilung ist ein Sonderfall der Beta-Verteilung
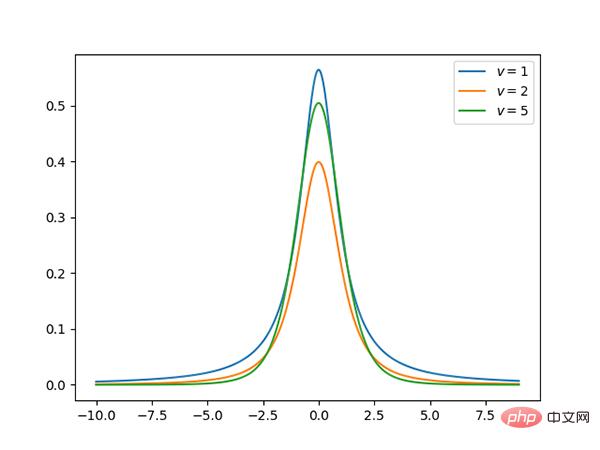
13.t-Verteilung (kontinuierlich)
Code: https://github.com/graykode/distribution-is-all-you-need/ blob/master /student-t.py
t Die Verteilung ist symmetrisch, glockenförmig, ähnlich der Normalverteilung, hat aber schwerere Enden, was bedeutet, dass sie mit größerer Wahrscheinlichkeit Werte erzeugt, die deutlich unter dem Mittelwert liegen.
über: https://github.com/graykode/distribution-is-all-you-needa
Das obige ist der detaillierte Inhalt von13 Wahrscheinlichkeitsverteilungen, die beim Deep Learning beherrscht werden müssen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

