Heim >Technologie-Peripheriegeräte >KI >Erweitern Sie Ihr Wissen! Maschinelles Lernen mit logischen Regeln
Erweitern Sie Ihr Wissen! Maschinelles Lernen mit logischen Regeln
- 青灯夜游nach vorne
- 2023-04-01 22:07:422079Durchsuche
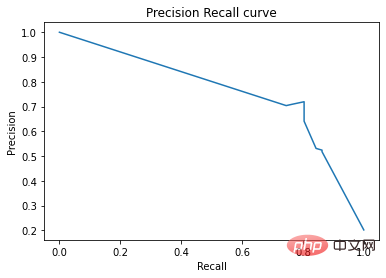
Auf der Precision-Recall-Kurve werden dieselben Punkte mit unterschiedlichen Achsen aufgetragen. Warnung: Der erste rote Punkt links (0 % Rückruf, 100 % Präzision) entspricht 0 Regeln. Der zweite Punkt links ist die erste Regel und so weiter.
Skope-rules verwendet ein Baummodell, um Regelkandidaten zu generieren. Erstellen Sie zunächst einige Entscheidungsbäume und betrachten Sie die Pfade vom Wurzelknoten zu internen Knoten oder Blattknoten als Regelkandidaten. Diese Kandidatenregeln werden dann nach einigen vordefinierten Kriterien wie Präzision und Rückruf gefiltert. Nur diejenigen, deren Präzision und Erinnerung über ihren Schwellenwerten liegen, werden beibehalten. Abschließend wird eine Ähnlichkeitsfilterung angewendet, um Regeln mit ausreichender Diversität auszuwählen. Im Allgemeinen werden Skope-Regeln angewendet, um die zugrunde liegenden Regeln für jede Grundursache zu lernen.
Projektadresse: https://github.com/scikit-learn-contrib/skope-rules
- Skope-rules ist ein Python-Modul für maschinelles Lernen, das auf scikit-learn basiert und unter 3-Klausel-BSD veröffentlicht wird Erlaubnis.
- Skope-rules zielt darauf ab, logische, interpretierbare Regeln zum „Definieren“ der Zielkategorie zu lernen, d. h. Instanzen dieser Kategorie mit hoher Genauigkeit zu erkennen.
- Skope-Regeln sind ein Kompromiss zwischen der Interpretierbarkeit von Entscheidungsbäumen und den Modellierungsfähigkeiten von Zufallswäldern.
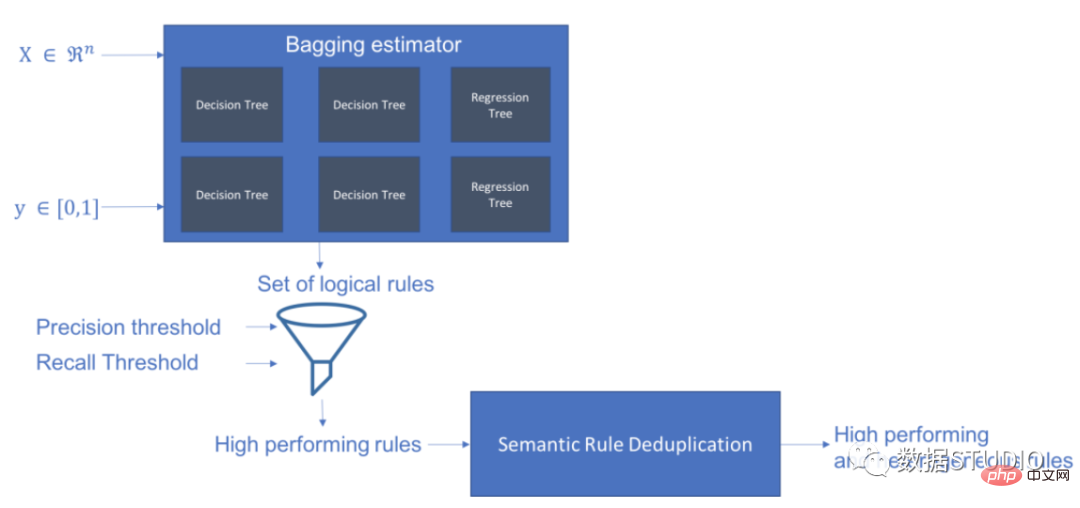
schema
Installation
Sie können pip verwenden, um die neuesten Ressourcen zu erhalten:
pip install skope-rules
Quick Start
SkopeRules können verwendet werden, um Klassen mit logischen Regeln zu beschreiben:
from. sklear n .datasets import load_iri s UFrom Skrules Import Skoperules
dataset = load_iris ()
feature_names = ['SEPAL_LENGTH', 'SEPAL_WIDTH', 'Petal_length'] KClf = Skoperules (MAX_DEPTH_DUPLICATINOTALOW = 2,
n_estimators = 30,
precision_min = 0,3 ,
call_min=0,1,
feature_names=feature_names)
für idx, Arten in enumerate(dataset.target_names):
X, y = dataset.data, dataset.target
clf.fit(X, y == idx)
Regeln = clf.rules_[0:3]
print("Regeln für Iris", Art)
für Regel in Regeln:
print(rule)
print()
print(20*'=')
print()
 Hinweis:
Hinweis:
Wenn der folgende Fehler auftritt:
 Lösung:
Lösung:
Informationen zum Python-Importfehler: Der Name „six“ kann nicht aus „sklearn.externals“ importiert werden. Yun Duojun hat einen ähnlichen Fehler bei „Stack Overflow Question“ gefunden : https://stackoverflow.com/questions/61867945/
Die Lösung ist wie folgt
import six
import syssys.modules['sklearn.externals.six'] = six
import mlrose
Persönlicher Test ist gültig !
SkopeRules können auch als Prädiktoren verwendet werden, wenn die Methode „score_top_rules“ verwendet wird:
aus sklearn.datasets import load_boston
aus sklearn.metrics import precision_recall_curveaus matplotlib import pyplot as plt
aus skrules import SkopeRules
dataset = _boston( )
clf = skoperules (max_depth_duplicatinotallow = none,
n_estimators = 30,
precision_min = 0,2,
usw. min = 0,01,
feature_names = dataset.feature_names)
x, y = dataset.data, dataSet.target & gt; , y_train = X[:len(y)//2], y[:len(y)//2]
X_test, y_test = X[len(y)//2:], y[len(y)/ /2:]
clf.fit(X_train, y_train)
y_score = clf.score_top_rules(X_test) # Erhalten Sie eine Risikobewertung für jedes Testbeispiel
precision, Recall, _ = precision_recall_curve(y_test, y_score)
plt.plot(recall , Präzision)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision Recall Curve')
plt.show()
- Lösen Sie das Problem der binären Klassifizierung.
- Extrahieren Sie interpretierbare Entscheidungsregeln.
Dieser Fall ist in 5 Teile unterteilt Erläuterung der „Überlebensregeln“ (mithilfe von SkopeRules().rules_property).
- Leistungsanalyse (mit der Methode SkopeRules.predict_top_rules()). 🔜 geteilt
- vom sklearn.tree-Import DecisionTreeClassifier matplotlib.pyplot als plt importieren
- aus sklearn.metrics importieren roc_curve, precision_recall_curve aus matplotlib importieren cm
- numpy als np importieren aus sklearn.metrics importieren confusion_matrix
- aus IPython.display import display
- # Titanic-Daten importieren Daten = pd.read_csv('../data/titanic-train.csv')
Datenvorbereitung
# Zeilen mit fehlendem Alter löschen
data = data.query('Age == Age')
# Codierung für Variable Sex erstellen Wert
data['isFemale'] = (data['Sex'] == 'female') * 1
# Unvaried Embarked erstellt codierten Wert
data = pd.concat(
[data,
pd.get_dummies(data. loc [:,'Embarked'],
dummy_na=False,
prefix='Embarked',
prefix_sep='_')],
axis=1
)
# Nicht verwendete Variablen löschen
data = data.drop( ['Name ', 'Ticket', 'Cabin',
'PassengerId', 'Sex', 'Embarked'],
axis = 1)# Trainings- und Testsätze erstellen
X_train, X_test, y_train, y_test = train_test_split(
data. drop(['Survived'], axis=1),data['Survived'],
test_size=0.25, random_state=42)
feature_names = X_train.columns
print('Spaltennamen sind: ' + ' '. join(feature_names.tolist())+'.')
print('Form des Trainingssatzes ist: ' + str(X_train.shape) + '.')
Spaltennamen sind: Pclass Age SibSp Parch Fare
isFemale Embarked_C Embarked_Q Embarked_S.
Die Form des Trainingssatzes ist: (535, 9).
Modelltraining
# Trainieren Sie einen Gradienten-Boosting-Klassifikator für Benchmark-Tests .fit(X_train, y_train)
# Trainiere einen zufälligen Waldklassifizierer für das Benchmarking
random_forest_clf = RandomForestClassifier(random_state=42, n_estimators=30, max_ Depth = 5)
random_forest_clf.fit(X_train , y_train)
# Trainiere einen Entscheidungsbaum Klassifikator für Benchmarking
decision_tree_clf = DecisionTreeClassifier(random_state=42, max_third = 5)
decision_tree_clf.fit(X_train, y_train)
# Trainieren Sie eine Skope-Regeln-verstärkende Klassifizierung
skope_rules_clf = SkopeRules(feature_names=feature_names, random_state= 42, n_schätzer =30,
call_min=0,05, precision_min=0,9,max_samples=0,7,
max_ Depth_duplicatinotallow= 4, max_ Depth = 5)
skope_rules_clf.fit(X _train, y_train)
# Vorhersage berechnen. Punktzahl
gradient_boost_scoring = gradient_boost_clf.predict_proba( X_test)[:, 1]random_forest_scoring = random_forest_clf.predict_proba (X_test)[:, 1] n")
# Drucken diese Regeln
rules_explanations = [
"Weiblich unter 3 Jahren und unter 37 Jahren in der ersten oder zweiten Klasse. „
“Frauen ab 3 Jahren reisen in der ersten oder zweiten Klasse und zahlen mehr als 26 Euro. „
„Frau, die in der ersten oder zweiten Klasse reist und mehr als 29 Euro bezahlt.“ „
„Frau, die über 39 Jahre alt ist und in der ersten oder zweiten Klasse reist. "
]
print('Die vier leistungsstärksten „Titanic-Überlebensregeln“ lauten wie folgt:/n')
für i_rule, Regel in enumerate(skope_rules_clf.rules_[:4])
print(rule[ 0])
print('->'+rules_explanations[i_rule]+ 'n')
Mit SkopeRules 9 Regeln erstellen
Die besten 4 „Titanic Survival Rules“ sind wie folgt:
Alter und P-Klasse > 0,5-> Frauen unter 3 Jahren und unter 37 Jahren
Alter > ;= 2,5 und isFemale > 0,5
-> Frauen über 3 Jahre, die in der ersten oder zweiten Klasse reisen und mehr als 26 Euro bezahlen.
Tarif > 29,356250762939453
und Pclass 0,5
-> Frauen, die mehr als 29 Euro für die erste oder zweite Klasse bezahlen.
Alter > 38,5 und Klasse und weiblich > 0,5
->
def compute_y_pred_from_query(X, Regel):
score = np.zeros(X.shape[0])
X = X.reset_index(drop=True)
score[list(X.query(rule).index)] = 1
return(score)
def compute_performances_from_y_pred(y_true, y_pred, index_name='default_index'):
df = pd.DataFrame(data=
{
'precision':[sum(y_true * y_pred)/sum(y_pred )],
'recall':[sum(y_true * y_pred)/sum(y_true)]
},
index=[index_name],
columns=['precision', 'recall']
)
return(df) ?? _performances_from_y_pred( y_test, y_test_pred, 'test_set')],
axis=0)
return(performances)
print('Präzision = 0,96 bedeutet, dass 96 % der durch die Regel identifizierten Personen Überlebende sind.')
print(' Recall = 0,12 bedeutet, dass die durch die Regel identifizierten Überlebenden 12 % der gesamten Überlebenden ausmachen.')
für i in range(4):
print('Rule '+str(i+1)+':')
display(compute_train_test_query_performances(X_train, y_train,
X_test, y_test,
skope_rules_clf.rules_[i][ 0])
)
Precision = 0,96 bedeutet, dass 96 % der durch die Regeln bestimmten Personen Überlebende sind.
Recall = 0,12 bedeutet, dass die durch die Regel identifizierten Überlebenden 12 % der Gesamtüberlebenden ausmachen. Modellleistungstests 'skope-rules']):
gradient = np.linspace(0, 1, 10)
color_list = [ cm.tab10(x) für x im Farbverlauf ]
fig, axis = plt.subplots(1, 2, figsize=(12, 5),
sharex=True, sharey=True)
ax = axis[0]
n_line = 0
für i_score, Score in enumerate(scores_with_line):
n_line = n_line + 1
fpr, tpr, _ = roc_curve(y_true, Score)
ax.plot(fpr, tpr, linestyle='-.', c=color_list[i_score], lw=1, label=labels_with_line[i_score])für i_score, Score in enumerate( scores_with_points):
fpr, tpr, _ = roc_curve(y_true, score)
ax.scatter(fpr[:-1], tpr[:-1], c=color_list[n_line + i_score], s=10, label= labels_with_points[i_score])ax.set_title("ROC", fnotallow=20)
ax.set_ylabel('True-Positiv-Rate (Rückruf)', fnotallow=18 ) ax.legend(loc='lower center', fnotallow=8)
ax.legend(loc='lower center', fnotallow=8)
ax = axis[1]
n_line = 0für i_score, Punkte in enumerate(scores_with_line):
n_line = n_line + 1
precision, Recall , _ = precision_recall_curve(y_true, score)
ax.step(recall, precision, linestyle='-.', c=color_list[i_score], lw=1, where='post', label=labels_with_line[i_score])
für i_score, Punktzahl in enumerate(scores_with_points):
precision, Recall, _ = precision_recall_curve(y_true, score)
ax.scatter(recall, precision, c=color_list[n_line + i_score], s=10, label=labels_with_points[i_score ])
ax.set_title("Precision-Recall", fnotallow=20)
ax.set_xlabel('Recall (True Positive Rate)', fnotallow=18)
ax.set_ylabel('Precision', fnotallow=18)
ax .legend(loc='lower center', fnotallow=8)
plt.show()
plot_titanic_scores(y_test,
scores_with_line=[gradient_boost_scoring, random_forest_scoring, Decision_tree_scoring],
scores_with_points=[skope_rules_scoring]
)
Auf der ROC-Kurve entspricht jeder rote Punkt der Anzahl der aktivierten Regeln (aus Skope-Regeln). Der niedrigste Punkt ist beispielsweise der Ergebnispunkt einer Regel (der besten). Der zweitniedrigste Punkt ist der 2-Regel-Ergebnispunkt und so weiter.
Auf der Precision-Recall-Kurve werden dieselben Punkte mit unterschiedlichen Koordinatenachsen aufgetragen. Warnung: Der erste rote Punkt links (0 % Rückruf, 100 % Präzision) entspricht 0 Regeln. Der zweite Punkt links ist die erste Regel und so weiter.
Aus diesem Beispiel lassen sich einige Schlussfolgerungen ziehen.
- Skope-Regeln sind leistungsfähiger als Entscheidungsbäume.
- skope-rules funktionieren ähnlich wie Random Forest/Gradient Boosting (in diesem Beispiel).
- Durch die Verwendung von 4 Regeln kann eine sehr gute Leistung erzielt werden (61 % Rückruf, 94 % Präzision) (in diesem Beispiel).
n_rule_chosen = 4
y_pred = skope_rules_clf.predict_top_rules(X_test, n_rule_chosen)
print('Die mit '+str(n_rule_chosen)+' ermittelten Regeln erreichten Leistungen sind die folgenden:')
compute_performances_from_y_pred (y_test, y_pred, ' test_set')
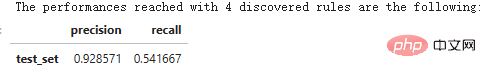
predict_top_rules(new_data, n_r) Methode wird verwendet, um die Vorhersage von new_data zu berechnen, die die ersten n_r Skope-Rules-Regeln enthält.
Das obige ist der detaillierte Inhalt vonErweitern Sie Ihr Wissen! Maschinelles Lernen mit logischen Regeln. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Technologietrends, die Sie im Jahr 2023 im Auge behalten sollten
- Wie künstliche Intelligenz Rechenzentrumsteams neue Alltagsaufgaben beschert
- Können künstliche Intelligenz oder Automatisierung das Problem der geringen Energieeffizienz in Gebäuden lösen?
- OpenAI-Mitbegründer im Interview mit Huang Renxun: Die Argumentationsfähigkeiten von GPT-4 haben noch nicht die Erwartungen erfüllt
- Dank der OpenAI-Technologie übertrifft Bing von Microsoft Google im Suchverkehr

