Heim >Java >javaLernprogramm >Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

WBOYnach vorne: 2022-11-25 16:51:501424Durchsuche

Dieser Artikel vermittelt Ihnen relevantes Wissen über Java und stellt hauptsächlich den relevanten Inhalt zu Sequenztabellen und verknüpften Listen vor. Eine Sequenztabelle ist ein Array, das eine Speichereinheit mit einer kontinuierlichen physischen Adresse verwendet, um Datenelemente nacheinander zu speichern Werfen Sie einen Blick auf die lineare Struktur. Ich hoffe, sie wird für alle hilfreich sein.

Empfohlenes Lernen: „Java-Video-Tutorial“

1. Lineare Liste

Eine lineare Liste ist eine endliche Folge von n Datenelementen mit denselben Eigenschaften. Lineare Tabellen sind in der Praxis weit verbreitete Datenstrukturen: Sequenzliste, verknüpfte Liste, Stapel, Warteschlange, Zeichenfolge ...

Eine lineare Tabelle ist logischerweise eine lineare Struktur, das heißt eine kontinuierliche gerade Linie. Die physische Struktur ist jedoch nicht unbedingt kontinuierlich. Wenn lineare Tabellen physisch gespeichert werden, werden sie normalerweise in Form von Arrays und verknüpften Strukturen gespeichert.

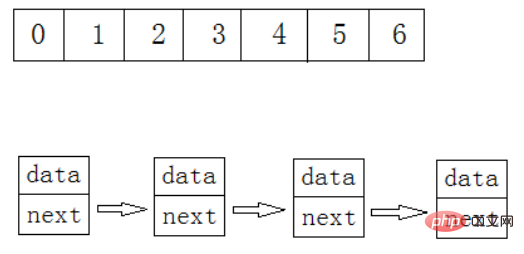
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

2. Die Sequenzliste

ist eigentlich ein Array . [Hinzufügen, löschen, prüfen und ändern] Warum schreiben Sie dann immer noch eine Sequenztabelle? Es ist anders. Wenn Sie es in eine Klasse schreiben, können Sie in Zukunft objektorientiert werden.

2.1 Konzept und Struktur

Eine Sequenztabelle ist eine lineare Struktur, die eine Speichereinheit mit kontinuierlichen physischen Adressen verwendet, um Datenelemente der Reihe nach zu speichern. Schließen Sie das Hinzufügen, Löschen, Überprüfen und Ändern von Daten im Array ab.

Sequenztabellen können im Allgemeinen unterteilt werden in:

Statische Sequenztabellen: Verwenden Sie Array-Speicher mit fester Länge.
Dynamische Sequenztabelle: Verwenden Sie dynamisch geöffneten Array-Speicher.

Die statische Sequenztabelle eignet sich für Szenarien, in denen bekannt ist, wie viele Daten gespeichert werden müssen.

Das Array fester Länge der statischen Sequenztabelle führt dazu, dass N auf eine große Größe festgelegt wird. Es wird zu viel Platz verschwendet. und zu wenig Platz ist nicht genug.

Im Gegensatz dazu sind dynamische Sequenztabellen flexibler und können Platz je nach Bedarf dynamisch zuweisen.

2.2 Schnittstellenimplementierung

Im Folgenden sind die Schnittstellen aufgeführt die unterstützt werden müssen.

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

Hier zerlegen wir sie einzeln. Out:

public class MyArrayList {

    public int[] elem;
    public int usedSize;//有效的数据个数

    public MyArrayList() {
        this.elem = new int[10];
    }
    // 打印顺序表public void display() {
    
    }
    System.out.println();}// 获取顺序表长度public int size() {
    return 0;}// 在 pos 位置新增元素public void add(int pos, int data) {}// 判定是否包含某个元素public boolean contains(int toFind) {
    return true;}// 查找某个元素对应的位置public int search(int toFind) {
    return -1;}// 获取 pos 位置的元素public int getPos(int pos) {
    return -1;}// 给 pos 位置的元素设为 valuepublic void setPos(int pos, int value) {}//删除第一次出现的关键字keypublic void remove(int toRemove) {}// 清空顺序表public void clear() {}}

Das ist die Grundstruktur unserer Sequenztabelle. Lassen Sie uns die Funktionen der Sequenztabelle einzeln aufschlüsseln:

Drucken Sie die Datentabelle:

public void display() {
    for (int i = 0; i < this.usedSize; i++) {
        System.out.print(this.elem[i] + " ");
    }
    System.out.println();}

Ermitteln Sie die Länge der Sequenztabelle:

public int size() {
    return this.usedSize;}

Fügen Sie ein Element an der Position pos hinzu:

public void add(int pos, int data) {
    if(pos < 0 || pos > this.usedSize) {
        System.out.println("pos 位置不合法");
        return;
    }
    if(isFull()){
        this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
    }
    for (int i = this.usedSize-1; i >= pos; i--) {
        this.elem[i + 1] = this.elem[i];
    }
    this.elem[pos] = data;
    this.usedSize++;}//判断数组元素是否等于有效数据个数public boolean isFull() {
    return this.usedSize == this.elem.length;}

Beurteilen Sie, ob ein bestimmtes Element vorhanden ist ist enthalten:

public boolean contains(int toFind) {
    for (int i = 0; i < this.usedSize; i++) {
        if (this.elem[i] == toFind) {
            return true;
        }
    }
    return false;}

Finden Sie die Position, die einem Element entspricht:

public int search(int toFind) {
    for (int i = 0; i < this.usedSize; i++) {
        if (this.elem[i] == toFind) {
            return i;
        }
    }
    return -1;}

Erhalten Sie das Element an der Pos-Position:

public int getPos(int pos) {
    if (pos < 0 || pos >= this.usedSize){
        System.out.println("pos 位置不合法");
        return -1;//所以 这里说明一下,业务上的处理，这里不考虑
    }
    if(isEmpty()) {
        System.out.println("顺序表为空！");
        return -1;
    }
    return this.elem[pos];}//判断数组链表是否为空public boolean isEmpty() {
    return this.usedSize == 0;}

Setzen Sie das Element an der Pos-Position als Wert:

public void setPos(int pos, int value) {
    if(pos < 0 || pos >= this.usedSize) {
        System.out.println("pos 位置不合法");
        return;
    }
    if(isEmpty()) {
        System.out.println("顺序表为空！");
        return;
    }
    this.elem[pos] = value;}//判断数组链表是否为空public boolean isEmpty() {
    return this.usedSize == 0;}

Löschen Sie das erste Vorkommen des Schlüsselwortschlüssels:

public void remove(int toRemove) {
    if(isEmpty()) {
        System.out.println("顺序表为空！");
        return;
    }
    int index = search(toRemove);//index记录删除元素的位置
    if(index == -1) {
        System.out.println("没有你要删除的数字！");
    }
    for (int i = index; i < this.usedSize - 1; i++) {
        this.elem[i] = this.elem[i + 1];
    }
    this.usedSize--;
    //this.elem[usedSize] = null;引用数组必须这样做才可以删除}

Sequenzliste löschen:

public void clear() {
    this.usedSize = 0;}

2.3 Probleme und Gedanken zu Sequenztabellen

Einfügung und Löschung in der Mitte/Kopf der Sequenztabelle, die zeitliche Komplexität ist O(N)
Steigend Kapazität erfordert die Beantragung von neuem Speicherplatz und das Kopieren von altem Speicherplatz. Es wird viel Verbrauch geben.
Die Kapazitätserweiterung erhöht sich im Allgemeinen um das Zweifache, und es wird zwangsläufig eine gewisse Menge an verschwendetem Platz entstehen. Beispielsweise beträgt die aktuelle Kapazität 100, und wenn sie voll ist, wird die Kapazität auf 200 erhöht. Wir fügen weiterhin 5 Daten ein, und später werden keine Daten eingefügt, sodass 95 Datenplätze verschwendet werden.

Denken: Wie kann man die oben genannten Probleme lösen? Zur Veranschaulichung ist unten die Struktur der verlinkten Liste aufgeführt. 3. Verknüpfte Liste 3.1 Das Konzept und die Struktur einer verknüpften Liste In der verknüpften Liste werden Links der Reihe nach implementiert.

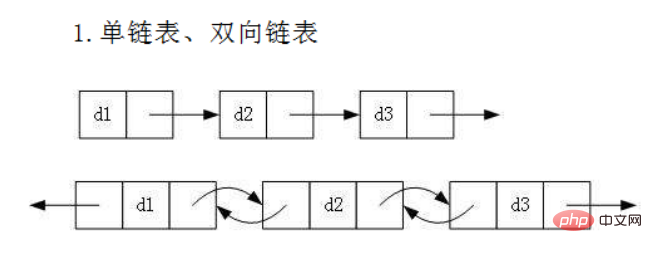
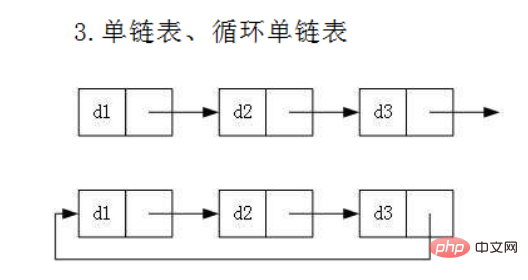
Tatsächlich sind die Strukturen verknüpfter Listen sehr unterschiedlich. Bei allgemeiner Aufteilung gibt es vier Typen:

Einseitig verknüpfte Liste

Doppelt verknüpfte ListeRundschreibende Liste 🔜 nichtzyklisch

Diese acht Typen sind: 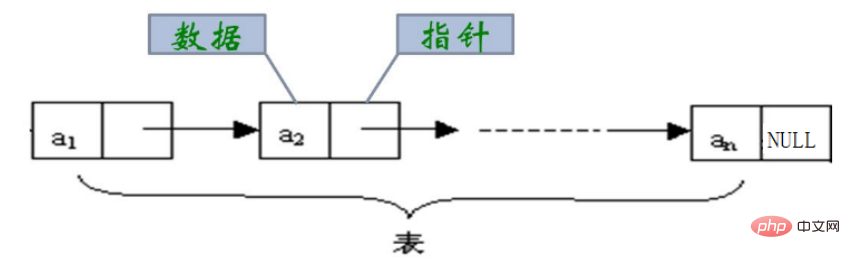Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

Einseitige führende Schleife

Einseitige führende Schleife
Einseitige führende Schleife, nicht-Schleife

Zweiseitige führende Schleife

Keine führende Schleife in beide Richtungen. Schleife
Zweiseitige führende Schleife, keine Schleife

Hinweis: Die oben fettgedruckten Wörter müssen wir lernen! ! !

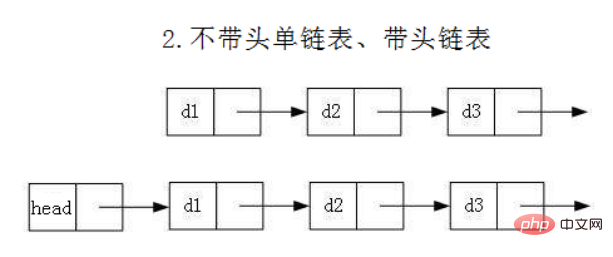
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

虽然有这么多的链表的结构，但是我们重点掌握两种:

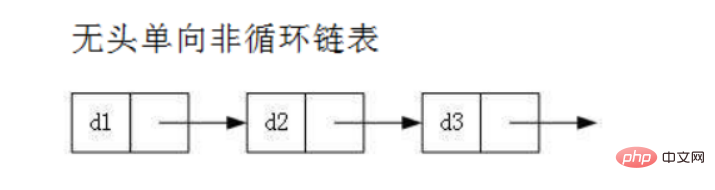
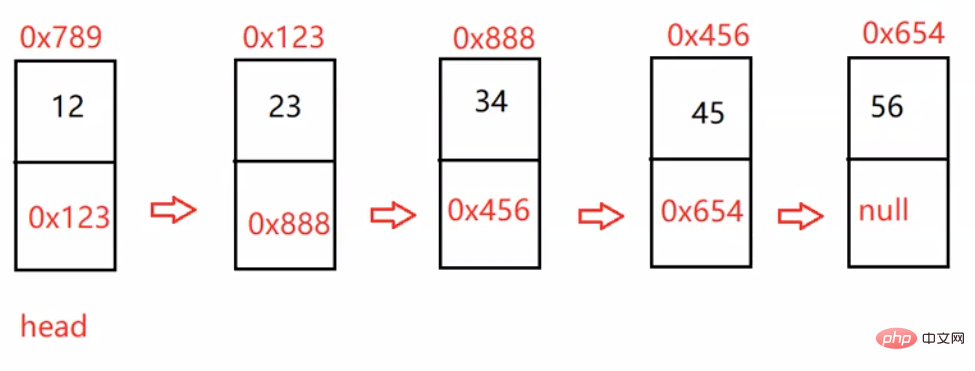
无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

head：里面存储的就是第一个节点(头节点)的地址

head.next：存储的就是下一个节点的地址

尾结点：它的next域是一个null

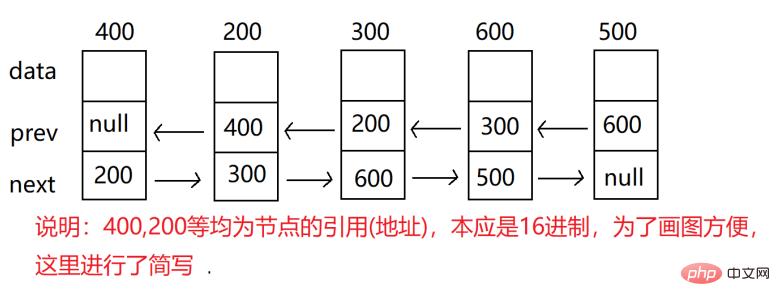
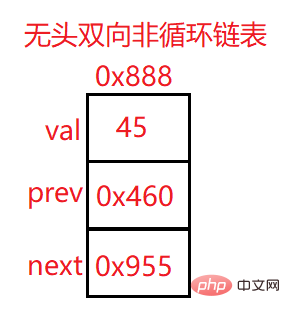
无头双向链表：在Java的集合框架库中LinkedList底层实现就是无头双向循环链表。

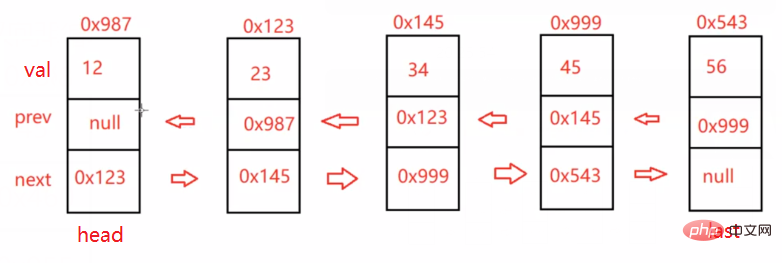
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

最上面的数字是我们每一个数值自身的地址。
prev：指向前一个元素地址
next：下一个节点地址
data：数据

3.2 链表的实现

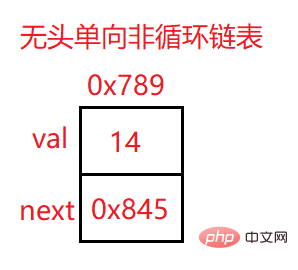
3.2.1无头单向非循环链表的实现

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

上面地址为改结点元素的地址
val：数据域
next：下一个结点的地址
head：里面存储的就是第一个结点(头结点)的地址
head.next：存储的就是下一个结点的地址

无头单向非循环链表实现:

class ListNode {
    public int val;
    public ListNode next;//ListNode储存的是结点类型

    public ListNode (int val) {
        this.val = val;
    }}public class MyLinkedList {
    public ListNode head;//链表的头引用

    public void creatList() {
        ListNode listNode1 = new ListNode(12);
        ListNode listNode2 = new ListNode(23);
        ListNode listNode3 = new ListNode(34);
        ListNode listNode4 = new ListNode(45);
        ListNode listNode5 = new ListNode(56);
        listNode1.next = listNode2;
        listNode2.next = listNode3;
        listNode3.next = listNode4;
        listNode4.next = listNode5;
        this.head = listNode1;
    }
    //查找是否包含关键字key是否在单链表当中
    public boolean contains(int key) {
        
        return true;
    }
    //得到单链表的长度
    public int size(){
        return -1;
    }
    //头插法
    public void addFirst(int data) {

    }
    //尾插法
    public void addLast(int data) {

    }
    //任意位置插入,第一个数据节点为0号下标
    public boolean addIndex(int index,int data) {
        return true;
    }
    //删除第一次出现关键字为key的节点
    public void remove(int key) {

    }
    //删除所有值为key的节点
    public ListNode removeAllKey(int key) {

    }
    //打印链表中的所有元素
    public void display() {

    }
    //清除链表中所有元素
    public void clear() {
        
    }}

上面是我们链表的初步结构(未给功能赋相关代码，大家可以复制他们到自己的idea中进行练习，答案在下文中) 这里我们将他们一个一个拿出来实现并实现！

打印链表中所有元素：

public void display() {
    ListNode cur = this.head;
    while(cur != null) {
        System.out.print(cur.val + " ");
        cur = cur.next;
    }
    System.out.println();}

查找是否包含关键字key是否在单链表当中：

public boolean contains(int key) {
    ListNode cur = this.head;
    while (cur != null) {
        if (cur.val == key) {
            return true;
        }
        cur = cur.next;
    }
    return false;}

得到单链表的长度：

public int size(){
    int count = 0;
    ListNode cur = this.head;
    while (cur != null) {
        count++;
        cur = cur.next;
    }
    return count;}

头插法(一定要记住绑定位置时一定要先绑定后面的数据避免后面数据丢失)：

public void addFirst(int data) {
    ListNode node = new ListNode(data);
    node.next = this.head;
    this.head = node;
    /*if (this.head == null) {
        this.head = node;
    } else {
        node.next = this.head;
        this.head = node;
    }*/}

尾插法：

public void addLast(int data) {
    ListNode node = new ListNode(data);
    if (this.head == null) {
        this.head = node;
    } else {
        ListNode cur = this.head;
        while (cur.next != null) {
            cur = cur.next;
        }
        cur.next = node;
    }}

任意位置插入,第一个数据结点为0号下标(插入到index后面一个位置)：

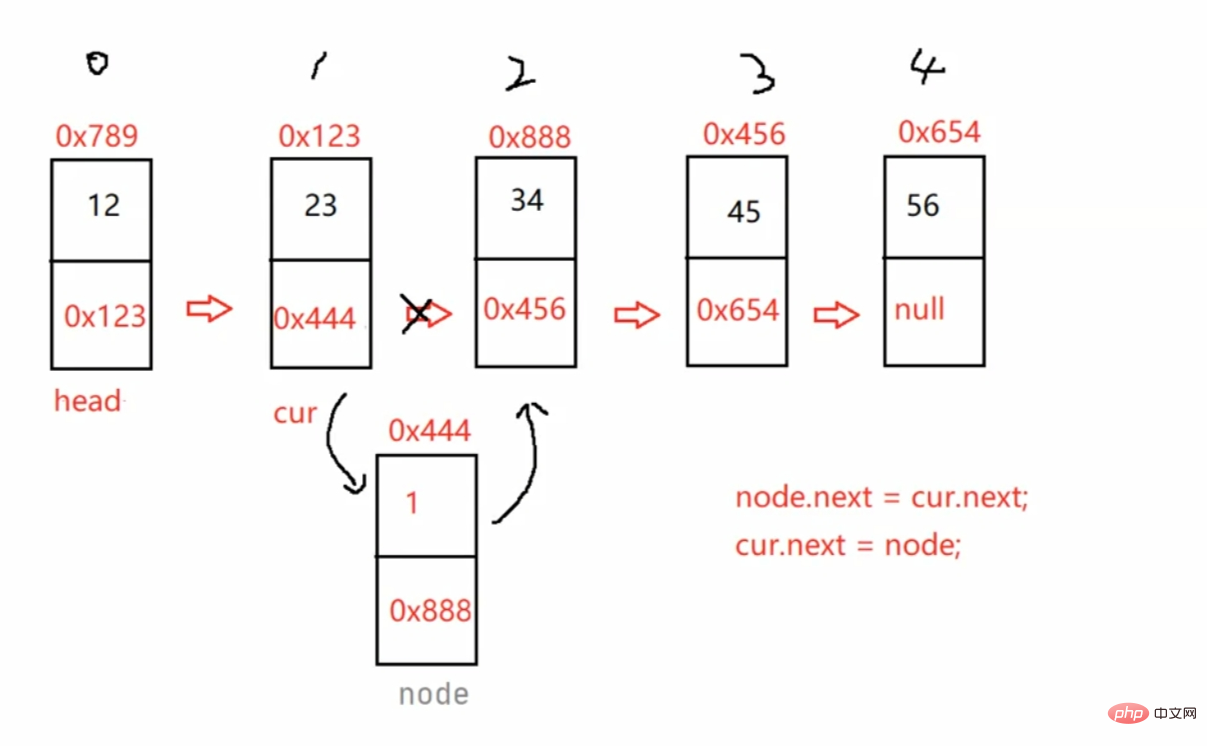
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

/**
 * 找到index - 1位置的节点的地址
 * @param index
 * @return
 */public ListNode findIndex(int index) {
    ListNode cur = this.head;
    while (index - 1 != 0) {
        cur = cur.next;
        index--;
    }
    return cur;}//任意位置插入,第一个数据节点为0号下标public void addIndex(int index,int data) {
    if(index < 0 || index > size()) {
        System.out.println("index 位置不合法！");
        return;
    }
    if(index == 0) {
        addFirst(data);
        return;
    }
    if(index == size()) {
        addLast(data);
        return;
    }
    ListNode cur = findIndex(index);
    ListNode node = new ListNode(data);
    node.next = cur.next;
    cur.next = node;}

注意：单向链表找cur时要-1，但双向链表不用直接返回cur就好

删除第一次出现关键字为key的结点：

/**
 * 找到 要删除的关键字key的节点
 * @param key
 * @return
 */public ListNode searchPerv(int key) {
    ListNode cur = this.head;
    while(cur.next != null) {
        if(cur.next.val == key) {
            return cur;
        }
        cur = cur.next;
    }
    return null;}//删除第一次出现关键字为key的节点public void remove(int key) {
    if(this.head == null) {
        System.out.println("单链表为空");
        return;
    }
    if(this.head.val == key) {
        this.head = this.head.next;
        return;
    }
    ListNode cur = searchPerv(key);
    if(cur == null) {
        System.out.println("没有你要删除的节点");
        return;
    }
    ListNode del = cur.next;
    cur.next = del.next;}

删除所有值为key的结点：

public ListNode removeAllKey(int key) {
    if(this.head == null) {
        return null;
    }
    ListNode prev = this.head;
    ListNode cur = this.head.next;
    
    while(cur != null) {
        if(cur.val == key) {
            prev.next = cur.next;
            cur = cur.next;
        } else {
            prev = cur;
            cur = cur.next;
        }
    }
        //最后处理头
    if(this.head.val == key) {
        this.head = this.head.next;
    }
    return this.head;}

清空链表中所有元素：

public void clear() {
    while (this.head != null) {
        ListNode curNext = head.next;
        head.next = null;
        head.prev = null;
        head = curNext;
    }
    last = null;}

3.2.2无头双向非循环链表实现：

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

上面的地址0x888为该结点的地址

val：数据域

prev：上一个结点地址

next：下一个结点地址

head：头结点一般指向链表的第一个结点

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

class ListNode {
    public int val;
    public ListNode prev;
    public ListNode next;

    public ListNode (int val) {
        this.val = val;
    }}public class MyLinkedList {
    public ListNode head;//指向双向链表的头结点
    public ListNode last;//只想双向链表的尾结点
    //打印链表
    public void display() {

    }
    //得到单链表的长度
    public int size() {
        return -1;
    }
    //查找是否包含关键字key是否在单链表当中
    public boolean contains(int key) {
        return true;
    }
    //头插法
    public void addFirst(int data) {

    }
    //尾插法
    public void addLast(int data) {

    }
    //删除第一次出现关键字为key的节点
    public void remove(int key) {

    }
    //删除所有值为key的节点
    public void removeAllKey(int key) {

    }
    //任意位置插入,第一个数据节点为0号下标
    public boolean addIndex(int index,int data) {
        return true;
    }
    //清空链表
    public void clear() {

    }}

打印链表：

public void display() {
    ListNode cur = this.head;
    while (cur != null) {
        System.out.print(cur.val + " ");
        cur = cur.next;
    }
    System.out.println();}

得到单链表的长度：

public int size() {
    ListNode cur = this.head;
    int count = 0;
    while (cur != null) {
        count++;
        cur = cur.next;
    }
    return count;}

查找是否包含关键字key是否在单链表当中:

public boolean contains(int key) {
    ListNode cur = this.head;
    while (cur != null) {
        if (cur.val == key) {
            return true;
        }
        cur = cur.next;
    }
    return false;}

头插法：

public void addFirst(int data) {
    ListNode node = new ListNode(data);
    if (this.head == null) {
        this.head = node;
        this.last = node;
    } else {
        node.next = this.head;
        this.head.prev = node;
        this.head = node;
    }}

尾插法：

public void addLast(int data) {
    ListNode node = new ListNode(data);
    if (this.head == null) {
        this.head = node;
        this.last = node;
    } else {
        ListNode lastPrev = this.last;
        this.last.next = node;
        this.last = this.last.next;
        this.last.prev = lastPrev;
        /**
         * 两种方法均可
         * this.last.next = node;
         * node.prev = this.last;
         * this.last = node;
         */
    }}

注：第一种方法是先让last等于尾结点再让他的前驱等于上一个地址而第二种方法是先使插入的尾结点的前驱等于上一个地址再使其等于尾结点

删除第一次出现关键字为key的结点:

public void remove(int key) {
    ListNode cur = this.head;
    while (cur != null) {
        if (cur.val == key) {
            if (cur == head) {
                head = head.next;
                if (head != null) {
                    head.prev = null;
                } else {
                    last = null;
                }
            } else if (cur == last) {
                last = last.prev;
                last.next = null;
            } else {
                cur.prev.next = cur.next;
                cur.next.prev = cur.prev;
            }
            return;
        }
        cur = cur.next;
    }}

删除所有值为key的结点:

public void removeAllKey(int key) {
    ListNode cur = this.head;
    while (cur != null) {
        if (cur.val == key) {
            if (cur == head) {
                head = head.next;
                if (head != null) {
                    head.prev = null;
                } else {
                    last = null;
                }
            } else if (cur == last) {
                last = last.prev;
                last.next = null;
            } else {
                cur.prev.next = cur.next;
                cur.next.prev = cur.prev;
            }
            //return;
        }
        cur = cur.next;
    }}

注：他和remove的区别就是删除完后是不是直接return返回，如果要删除所有的key值则不return，让cur继续往后面走。

任意位置插入,第一个数据节点为0号下标：

public void addIndex(int index,int data) {
    if (index < 0 || index > size()) {
        System.out.println("index 位置不合法");
    }
    if (index == 0) {
        addFirst(data);
        return;
    }
    if (index == size()) {
        addLast(data);
        return;
    }
    ListNode cur = searchIndex(index);
    ListNode node = new ListNode(data);
    node.next = cur;
    cur.prev.next = node;
    node.prev = cur.prev;
    cur.prev = node;}public ListNode searchIndex(int index) {
    ListNode cur = this.head;
    while (index != 0) {
        cur = cur.next;
        index--;
    }
    return cur;}

思路：先判断在头位置就头插在尾位置就尾插在中间就改变四个位置的值。

注意：单向链表找cur时要-1，但双向链表不用直接返回cur就好

清空链表：

public void clear() {
    while (this.head != null) {
        ListNode curNext = head.next;
        head.next = null;
        head.prev = null;
        head = curNext;
    }
    last = null;}

3.3 链表面试题

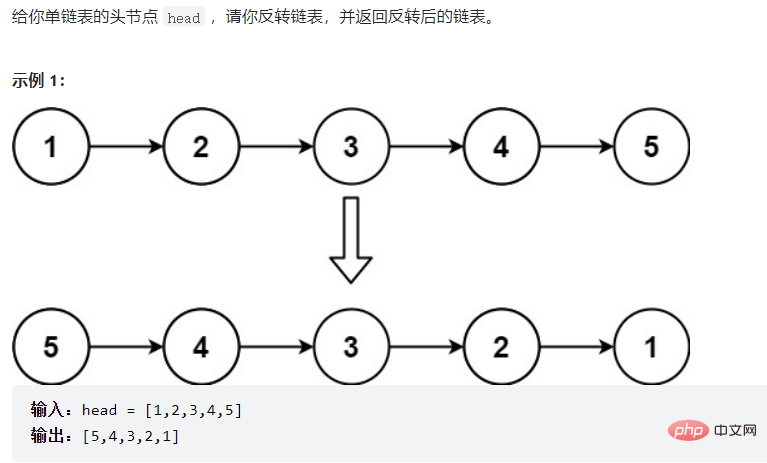
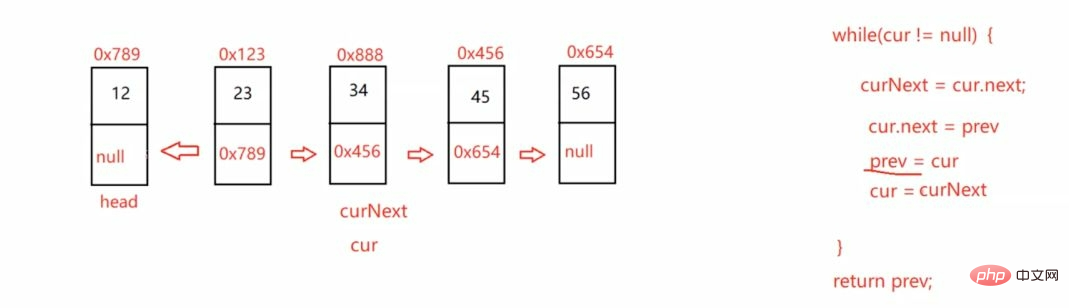
3.3.1反转链表：

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

这里的

cur = this.head;

prev = null;

curNext = cur.next;

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public ListNode reverseList() {
    if (this.head == null) {
        return null;
    }
    ListNode cur = this.head;
    ListNode prev = null;
    while (cur != null) {
        ListNode curNext = cur.next;
        cur.next = prev;
        prev = cur;
        cur = curNext;
    }
    return prev;}

3.3.2找到链表的中间结点：

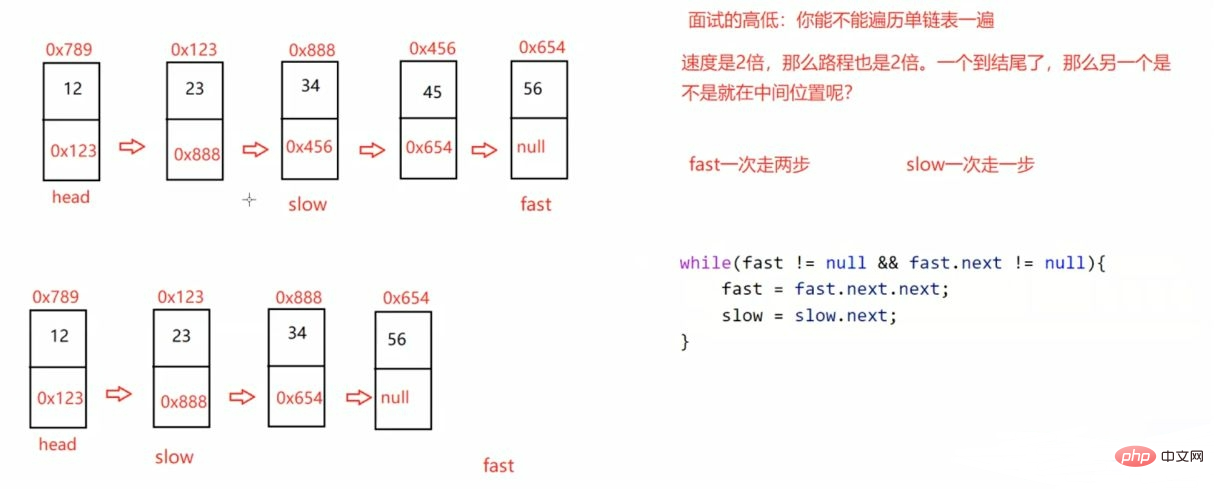
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public  ListNode middleNode() {
    if (head == null) {
        return null;
    }
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        if (fast == null) {
            return slow;
        }
        slow = slow.next;
    }
    return slow;}

3.3.3输入一个链表返回该链表中倒数第k个结点

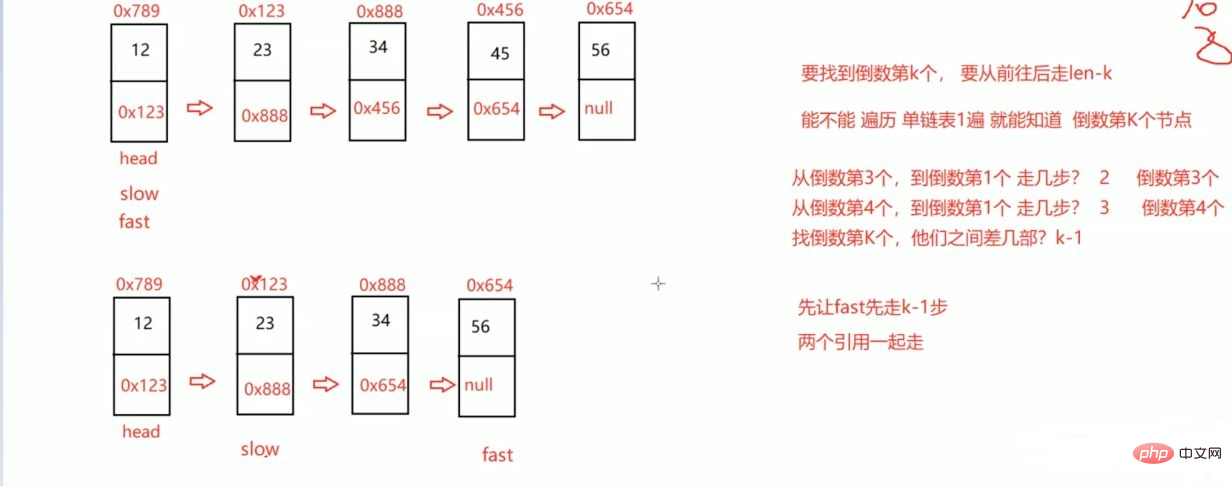
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public ListNode findKthToTail(ListNode head,int k) {
    if (k <= 0 || head == null) {
        return null;
    }
    ListNode fast = head;
    ListNode slow = head;
    while (k - 1 != 0) {
        fast = fast.next;
        if (fast == null) {
            return null;
        }
        k--;
    }
    while (fast.next != null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;}

3.3.4合并两个链表并变成有序的

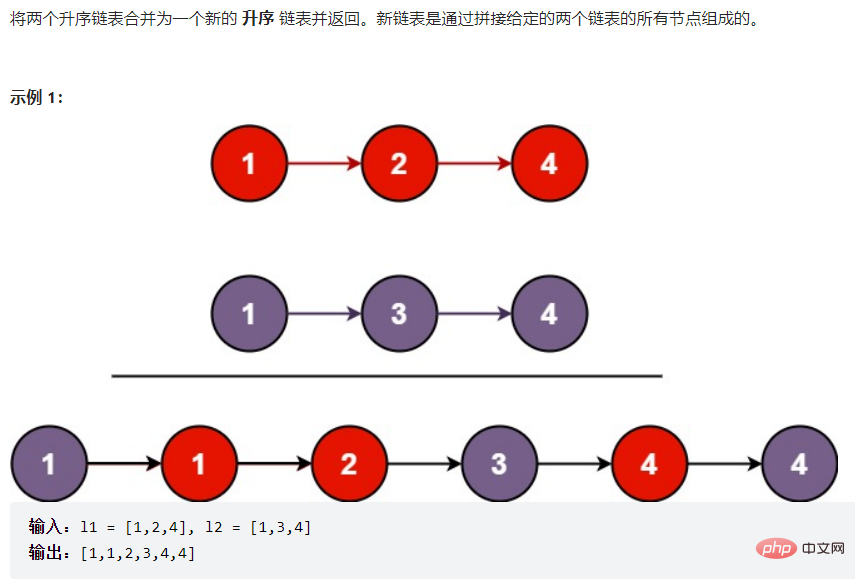
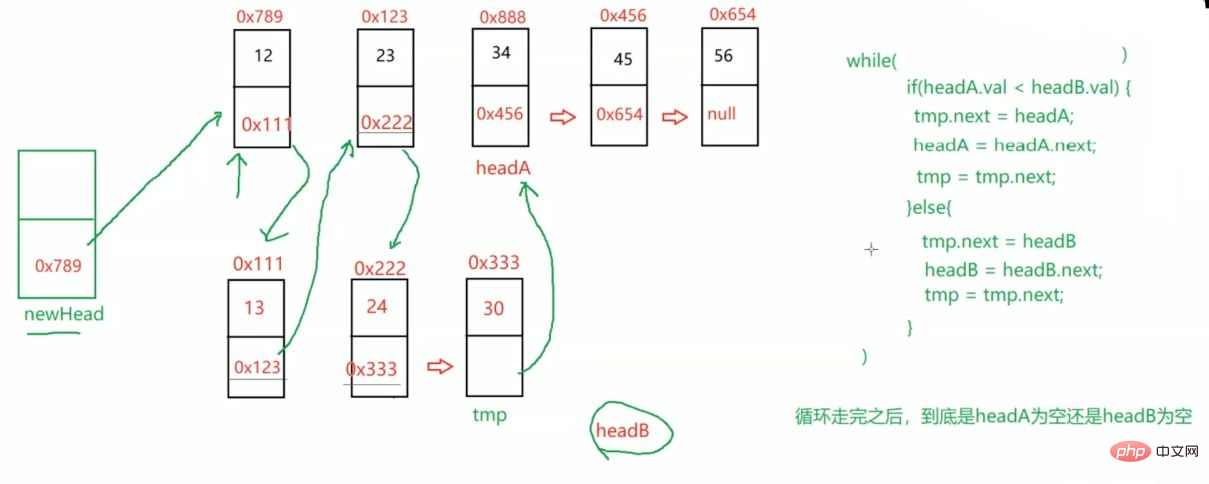
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public  static  ListNode mergeTwoLists(ListNode headA,ListNode headB) {
    ListNode newHead = new ListNode(-1);
    ListNode tmp = newHead;
    while (headA != null && headB != null) {
        if(headA.val <headB.val) {
            tmp.next = headA;
            headA = headA.next;
            tmp = tmp.next;
        } else {
            tmp.next = headB;
            headB = headB.next;
            tmp = tmp.next;
        }
    }
    if (headA != null) {
        tmp.next = headA;
    }
    if (headB != null) {
        tmp.next = headB;
    }
    return newHead.next;}

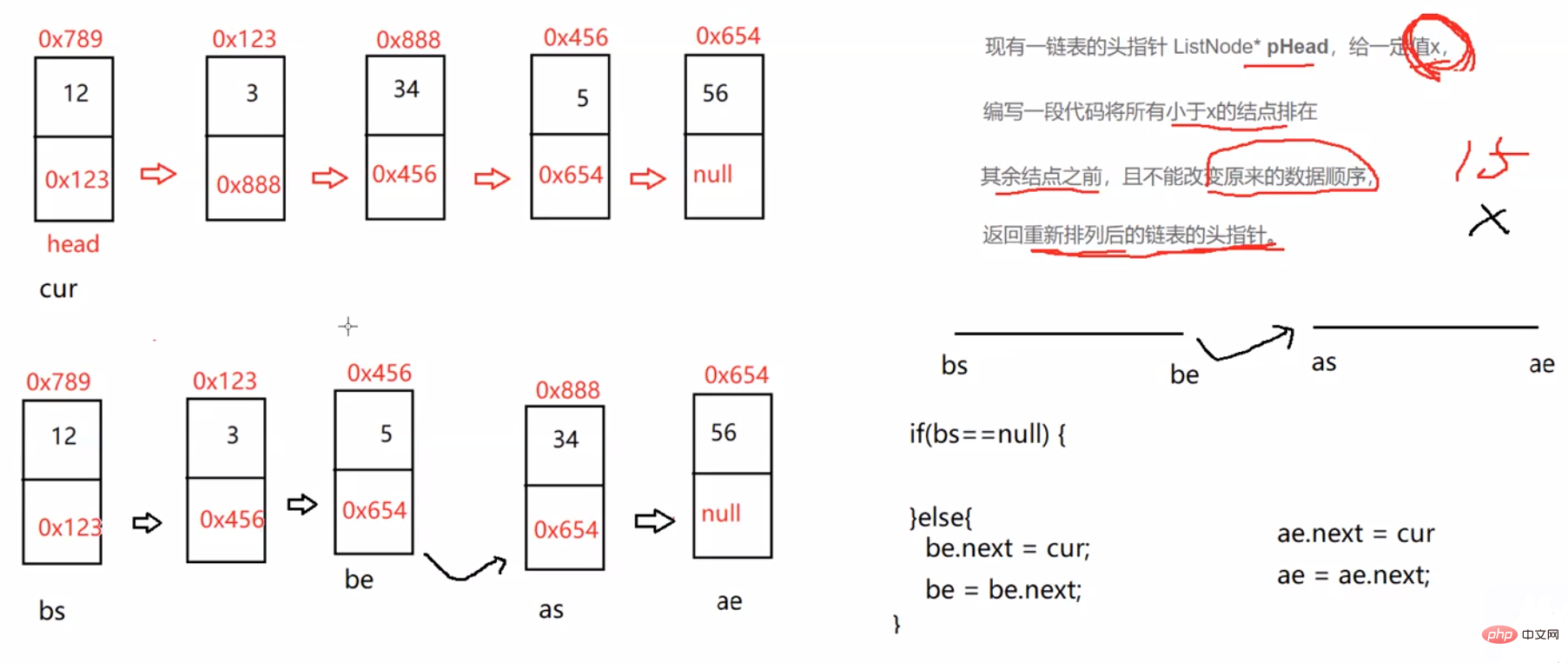
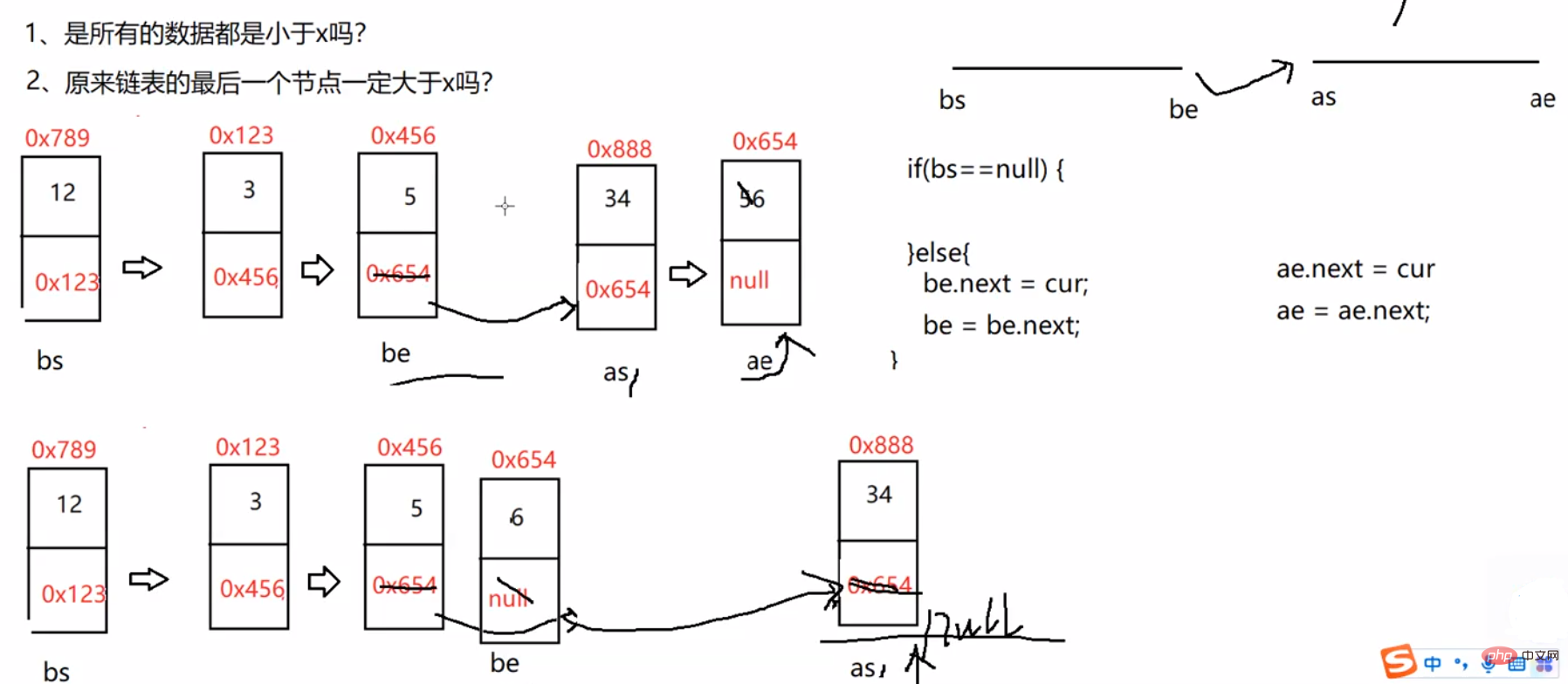
最后返回的是傀儡结点的下一个即newHead.next

3.3.5 编写代码，以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结点之前。(即将所有小于x的放在x左边，大于x的放在x右边。且他们本身的排序不可以变)

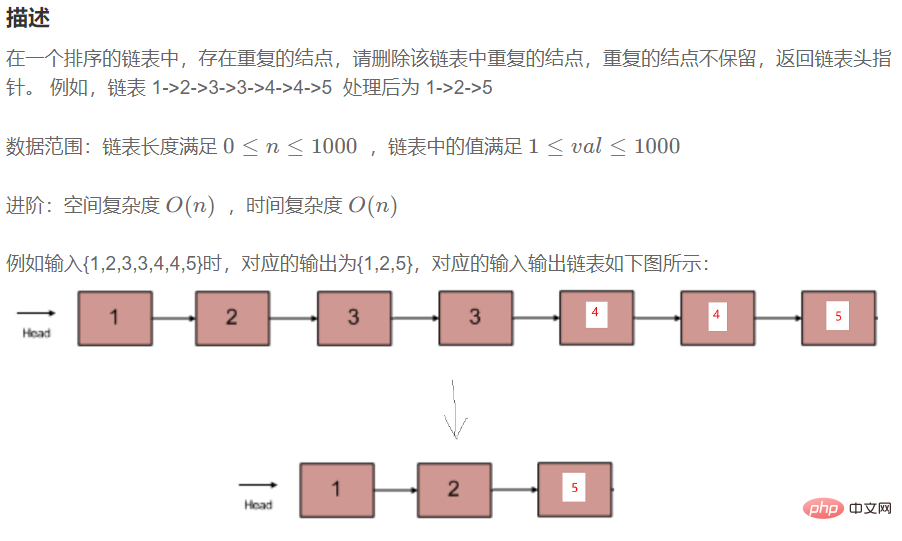
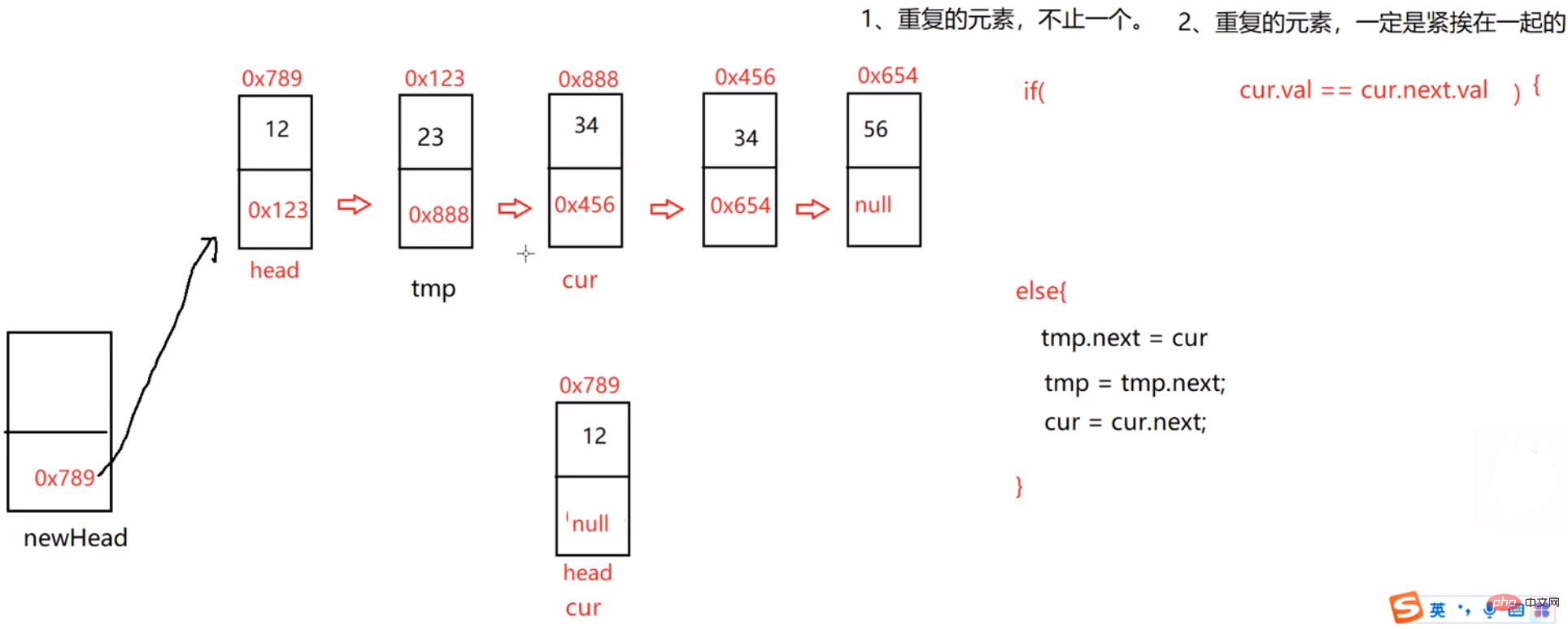
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

//按照x和链表中元素的大小来分割链表中的元素public ListNode partition(int x) {
    ListNode bs = null;
    ListNode be = null;
    ListNode as = null;
    ListNode ae = null;
    ListNode cur = head;
    while (cur != null) {
        if(cur.val < x){
            //1、第一次
            if (bs == null) {
                bs = cur;
                be = cur;
            } else {
                //2、不是第一次
                be.next = cur;
                be = be.next;
            }
        } else {
            //1、第一次
            if (as == null) {
                as = cur;
                as = cur;
            } else {
                //2、不是第一次
                ae.next = cur;
                ae = ae.next;
            }
        }
        cur = cur.next;
    }
    //预防第1个段为空
    if (bs == null) {
        return as;
    }
    be.next = as;
    //预防第2个段当中的数据，最后一个节点不是空的。
    if (as != null) {
        ae.next = null;
    }
    return be;}

3.3.6 在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。(有序的链表中重复的结点一定是紧紧挨在一起的)

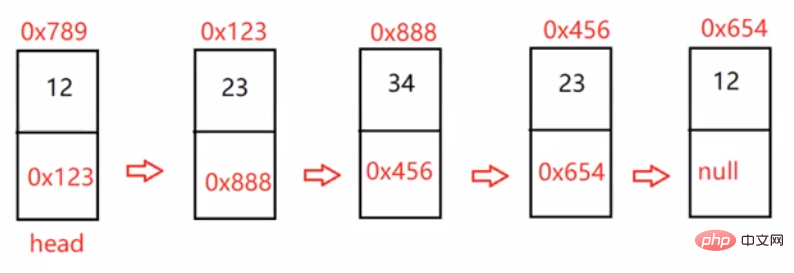
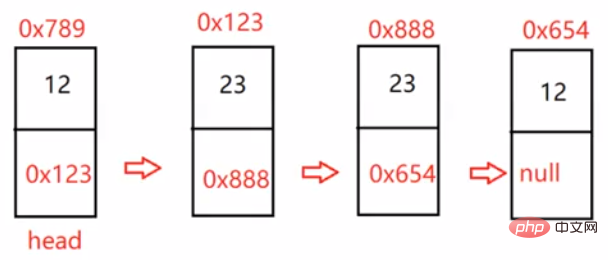
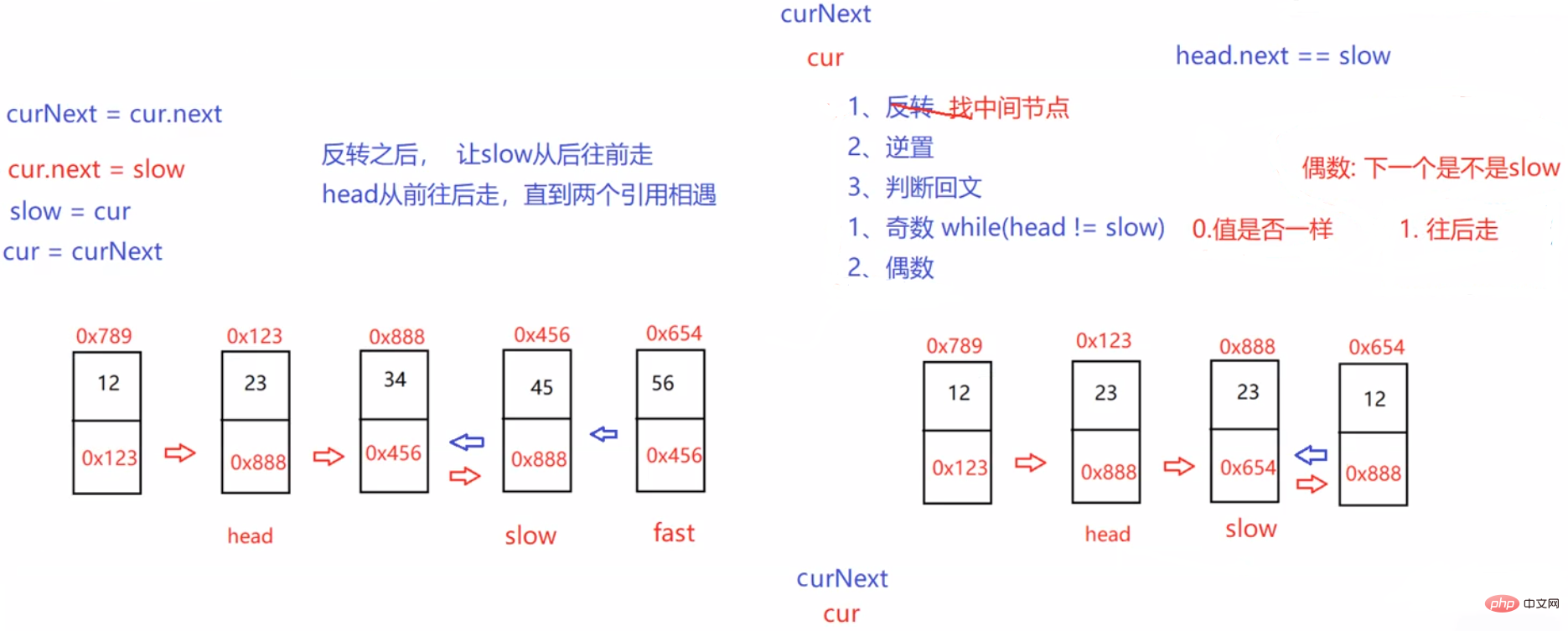
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public ListNode deleteDuplication() {
    ListNode cur = head;
    ListNode newHead = new ListNode(-1);
    ListNode tmp = newHead;
    while (cur != null) {
        if (cur.next != null && cur.val == cur.next.val) {
            while (cur.next != null && cur.val == cur.next.val) {
                cur = cur.next;
            }
            //多走一步
            cur = cur.next;
        } else {
            tmp.next = cur;
            tmp = tmp.next;
            cur = cur.next;
        }
    }
    //防止最后一个结点的值也是重复的
    tmp.next = null;
    return newHead.next;}

3.3.7 链表的回文结构。

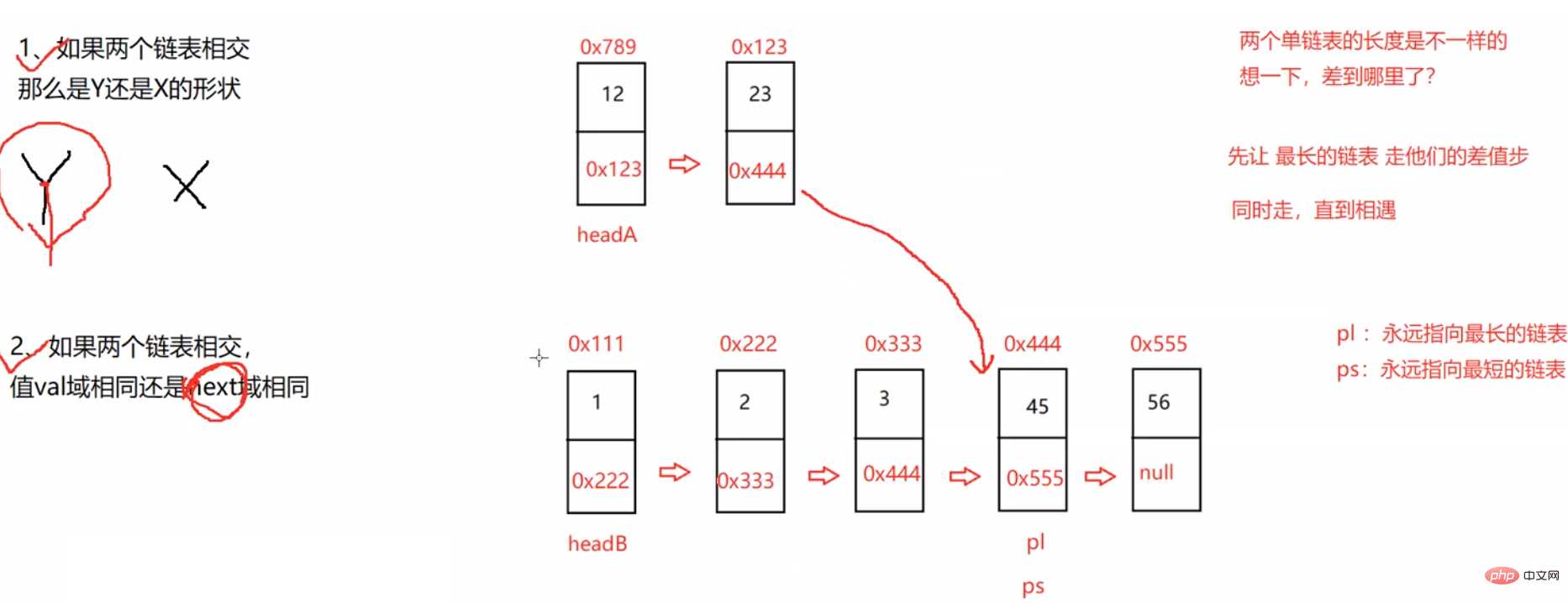
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public boolean chkPalindrome(ListNode head) {
    if (head == null) {
        return true;
    }
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    //slow走到了中间位置
    ListNode cur = slow.next;
    while (cur != null) {
        ListNode curNext = cur.next;
        cur.next = slow;
        slow = cur;
        cur = curNext;
    }
    //反转完成
    while (head != slow) {
        if(head.val != slow.val) {
            return false;
        } else {
            if (head.next == slow) {
                return true;
            }
            head = head.next;
            slow = slow.next;
        }
        return true;
    }
    return true;}

3.3.8 输入两个链表，找出它们的第一个公共结点。

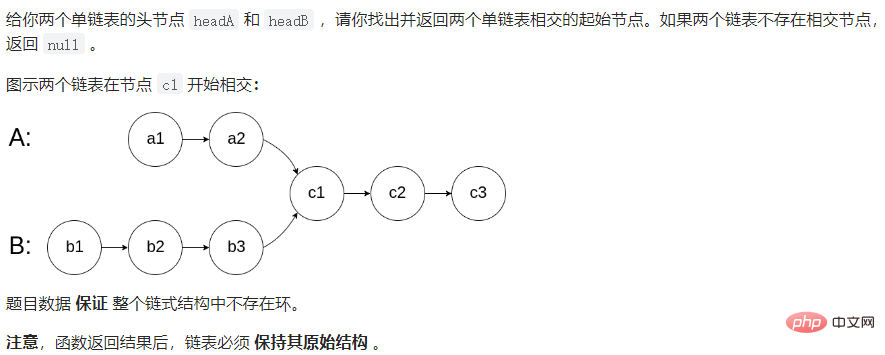
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

他是一个Y字形

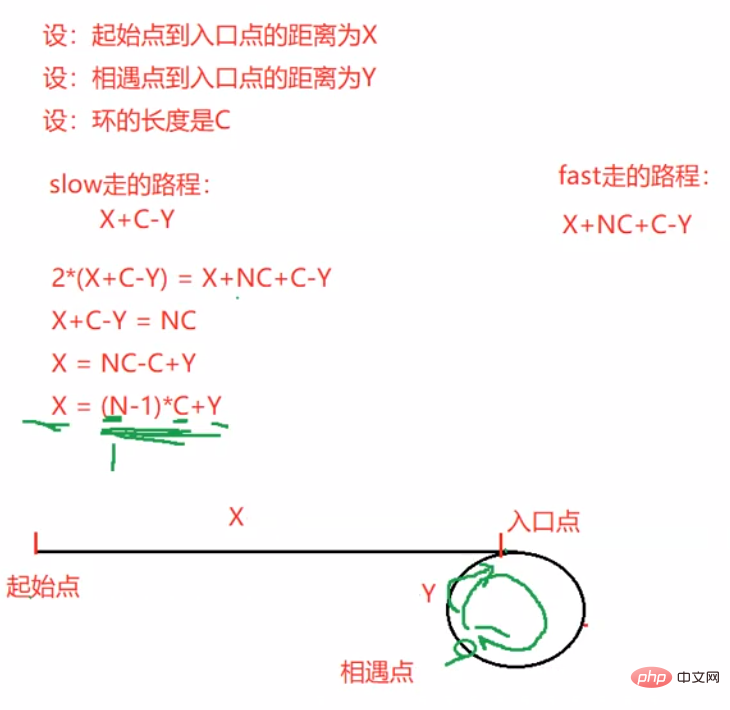
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    if (headA == null || headB == null) {
        return null;
    }
    ListNode pl = headA;
    ListNode ps = headB;
    int lenA = 0;
    int lenB = 0;
    //求lenA的长度
    while (pl != null) {
        lenA++;
        pl = pl.next;
    }
    pl = headA;
    //求lenB的长度
    while (ps != null) {
        lenB++;
        ps = ps.next;
    }
    ps = headB;
    int len = lenA - lenB;//差值步
    if (len < 0) {
        pl = headB;
        ps = headA;
        len = lenB - lenA;
    }
    //1、pl永远指向了最长的链表，ps永远指向了最短的链表   2、求到了插值len步
    //pl走差值len步
    while (len != 0) {
        pl = pl.next;
        len--;
    }
    //同时走直到相遇
    while (pl != ps) {
        pl = pl.next;
        ps = ps.next;
    }
    return pl;}

3.3.9 给定一个链表，判断链表中是否有环。

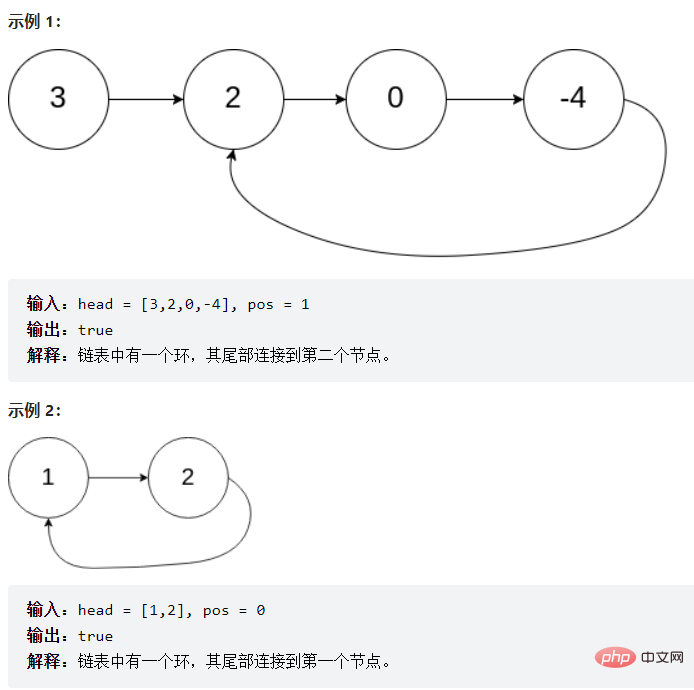
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

提问：为啥么fast一次走两步，不走三步？

答：如果链表只有两个元素他们则永远相遇不了(如上图的示例2)，而且走三步的效率没有走两步的效率高。

public boolean hasCycle(ListNode head) {
    if (head == null) {
        return false;
    }
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) {
            return true;
        }
    }
    return false;}

3.3.10 给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null

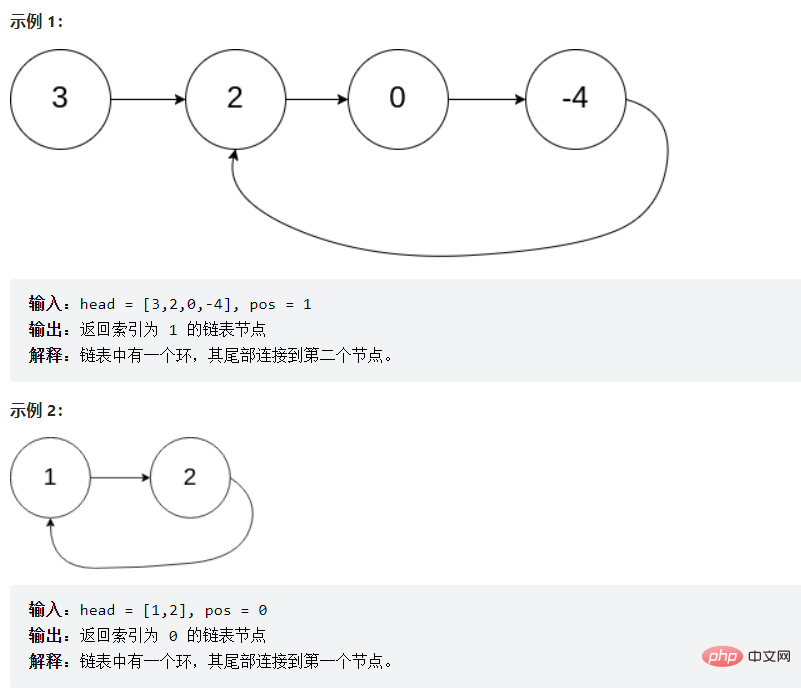
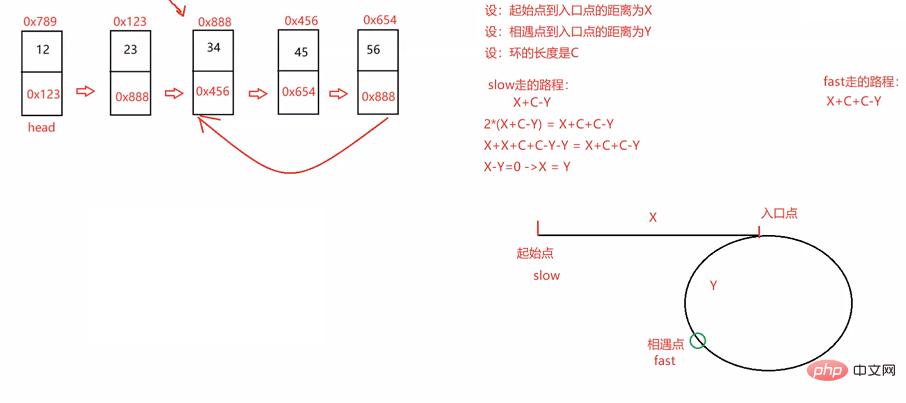
Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

public ListNode detectCycle(ListNode head) {
    if (head == null) {
        return null;
    }
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) {
            break;
        }
    }
    if (fast == null || fast.next == null) {
        return null;
    }
    fast = head;
    while (fast != slow) {
        fast = fast.next;
        slow = slow.next;
    }
    return fast;}

4. 顺序表和链表的区别和联系

4.1顺序表和链表的区别

顺序表：一白遮百丑

白：空间连续、支持随机访问

丑：

中间或前面部分的插入删除时间复杂度O(N)
增容的代价比较大。

链表：一(胖黑)毁所有

胖黑：以节点为单位存储，不支持随机访问

所有：

任意位置插入删除时间复杂度为O(1)
没有增容问题，插入一个开辟一个空间。

组织：

1、顺序表底层是一个数组，他是一个逻辑上和物理上都是连续的

2、链表是一个由若干结点组成的一个数据结构，逻辑上是连续的但是在物理上[内存上]是不一定连续的。

操作：

1、顺序表适合，查找相关的操作，因为可以使用下标，直接获取到某个位置的元素

2、链表适合于，频繁的插入和删除操作。此时不需要像顺序表一样，移动元素。链表的插入只需要修改指向即可。

3、顺序表还有不好的地方，就是你需要看满不满，满了要扩容，扩容了之后，不一定都能放完。所以，他空间上的利用率不高。

4.2数组和链表的区别

链表随用随取要一个new一个

而数组则不一样数组是一开始就确定好的

4.3AeeayList和LinkedList的区别

集合框架当中的两个类

集合框架就是将所有的数据结构，封装成Java自己的类

以后我们要是用到顺序表了直接使用ArrayList就可以。

推荐学习：《java视频教程》

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Java NULL 面向对象封装字符串循环指针数据结构接口栈对象 this idea

Stellungnahme：

Dieser Artikel ist reproduziert unter:csdn.net. Bei Verstößen wenden Sie sich bitte an admin@php.cn löschen

Vorheriger Artikel：Java-Datenstruktur, einfach verknüpfte Liste und OJ-FragenNächster Artikel：Java-Datenstruktur, einfach verknüpfte Liste und OJ-Fragen

In Verbindung stehende Artikel

Mehr sehen

Detaillierte Erläuterung der Java-Sequenzliste und der verknüpften Liste mit Beispielen

1. Lineare Liste

2. Die Sequenzliste

2.1 Konzept und Struktur

2.2 Schnittstellenimplementierung

2.3 Probleme und Gedanken zu Sequenztabellen

Einseitig verknüpfte Liste

3.2 链表的实现

3.2.1无头单向非循环链表的实现

3.2.2无头双向非循环链表实现：

3.3 链表面试题

3.3.1反转链表：

3.3.2找到链表的中间结点：

3.3.3输入一个链表 返回该链表中倒数第k个结点

3.3.4合并两个链表 并变成有序的

3.3.5 编写代码，以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结点之前 。(即将所有小于x的放在x左边，大于x的放在x右边。且他们本身的排序不可以变)

3.3.6 在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。(有序的链表中重复的结点一定是紧紧挨在一起的)

3.3.7 链表的回文结构。

3.3.8 输入两个链表，找出它们的第一个公共结点。

3.3.9 给定一个链表，判断链表中是否有环。

3.3.10 给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null

4. 顺序表和链表的区别和联系

4.1顺序表和链表的区别

4.2数组和链表的区别

4.3AeeayList和LinkedList的区别

In Verbindung stehende Artikel

3.3.3输入一个链表返回该链表中倒数第k个结点

3.3.4合并两个链表并变成有序的

3.3.5 编写代码，以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结点之前。(即将所有小于x的放在x左边，大于x的放在x右边。且他们本身的排序不可以变)

3.3.10 给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null