Die Universität für Wissenschaft und Technologie Chinas und Huawei Noah haben das Entropiegesetz vorgeschlagen, um den Zusammenhang zwischen der Leistung großer Modelle, der Datenkomprimierungsrate und dem Trainingsverlust aufzudecken.

Die AIxiv-Kolumne ist eine Kolumne, in der diese Website akademische und technische Inhalte veröffentlicht. In den letzten Jahren sind in der AIxiv-Kolumne dieser Website mehr als 2.000 Berichte eingegangen, die Spitzenlabore großer Universitäten und Unternehmen auf der ganzen Welt abdecken und so den akademischen Austausch und die Verbreitung wirksam fördern. Wenn Sie hervorragende Arbeiten haben, die Sie teilen möchten, können Sie gerne einen Beitrag leisten oder uns für die Berichterstattung kontaktieren. E-Mail für die Einreichung: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com China und Huaweis Arche Noah-Labor. Das Team von Professor Chen Enhong beschäftigt sich intensiv mit den Bereichen Data Mining und maschinelles Lernen und hat zahlreiche Artikel in führenden Fachzeitschriften und Konferenzen veröffentlicht, die mehr als 20.000 Mal zitiert wurden. Das Noah's Ark Laboratory ist das Huawei-Labor, das sich mit Grundlagenforschung zu künstlicher Intelligenz beschäftigt. Es verfolgt das Konzept, theoretische Forschung und Anwendungsinnovation gleichermaßen in den Vordergrund zu stellen, und setzt sich für die Förderung technologischer Innovationen und Entwicklungen im Bereich der künstlichen Intelligenz ein.

Daten sind der Grundstein für den Erfolg großer Sprachmodelle (LLMs), aber nicht alle Daten sind für das Modelllernen von Vorteil. Intuitiv wird erwartet, dass qualitativ hochwertige Proben eine bessere Effizienz beim LLM-Unterricht haben. Daher konzentrieren sich bestehende Methoden in der Regel auf eine qualitätsbasierte Datenauswahl. Die meisten dieser Methoden werten jedoch verschiedene Datenproben unabhängig voneinander aus und ignorieren dabei die komplexen kombinatorischen Effekte zwischen den Proben. Wie in Abbildung 1 dargestellt, kann die Kombination der einzelnen Stichproben aufgrund der Redundanz oder Inkonsistenz der gegenseitigen Informationen dennoch suboptimal sein, selbst wenn jede Stichprobe von perfekter Qualität ist. Obwohl die qualitätsbasierte Teilmenge aus allen drei Qualitätsproben besteht, ist das darin kodierte Wissen tatsächlich redundant und widersprüchlich. Im Gegensatz dazu kann ein anderer Datenteilsatz, der aus mehreren relativ minderwertigen, aber unterschiedlichen Stichproben besteht, für den LLM-Unterricht aussagekräftiger sein. Daher ist die qualitätsbasierte Datenauswahl nicht vollständig auf das Ziel einer Maximierung der LLM-Wissenserfassung ausgerichtet.

Und dieser Artikel zielt darauf ab, die intrinsische Beziehung zwischen LLM-Leistung und Datenauswahl aufzudecken. Inspiriert durch die Natur der LLM-Informationskomprimierung haben wir ein Entropiegesetz entdeckt, das die LLM-Leistung mit der Datenkomprimierungsrate und dem Verlust früherer Schritte des Modelltrainings verknüpft, was jeweils den Grad der Informationsredundanz des Datensatzes und den inhärenten Effekt widerspiegelt des LLM im Datensatz. Durch theoretische Ableitung und empirische Auswertung stellen wir fest, dass die Modellleistung umgekehrt mit dem Komprimierungsverhältnis der Trainingsdaten zusammenhängt, was normalerweise zu einem geringeren Trainingsverlust führt. Basierend auf den Erkenntnissen des Entropiegesetzes schlagen wir eine sehr effiziente und allgemeine Datenauswahlmethode für das Training von LLM namens ZIP vor, die darauf abzielt, vorzugsweise Datenteilmengen mit niedrigem Komprimierungsverhältnis auszuwählen. ZIP wählt in mehreren Schritten gierig verschiedene Daten aus und erhält so letztendlich eine Datenteilmenge mit guter Diversität.

Team: Chen Enhongs Team am National Key Laboratory of Cognitive Intelligence, University of Science and Technology of China, Huawei Noah's Ark Laboratory

Link zum Papier: https://arxiv.org/pdf/2407.06645

• Code-Link: https://github.com/USTC-StarTeam/ZIP
O Abbildung 1 tENTropiegesetz
Wir analysieren die theoretische Analyse des Zusammenhangs zwischen Datenkomprimierung und LLM-Leistung. Intuitiv wirken sich die Korrektheit und Vielfalt der Trainingsdaten auf die Leistung des endgültigen Modells aus. Gleichzeitig kann die LLM-Leistung nicht optimal sein, wenn die Daten schwerwiegende inhärente Konflikte aufweisen oder wenn das Modell die in den Daten kodierten Informationen nur unzureichend versteht. Basierend auf diesen Annahmen bezeichnen wir die Leistung von LLM als Z, die voraussichtlich beeinflusst wird durch:


Datenkomprimierungsverhältnis R: Intuitiv weisen Datensätze mit niedrigeren Komprimierungsverhältnissen auf eine höhere Informationsdichte hin.

Trainingsverlust L: Gibt an, ob die Daten für das Modell schwer zu merken sind. Unter demselben Basismodell ist ein hoher Trainingsverlust normalerweise auf das Vorhandensein von Rauschen oder inkonsistenten Informationen im Datensatz zurückzuführen.
• Datenkonsistenz C: Die Konsistenz der Daten spiegelt sich in der Entropie der Wahrscheinlichkeit des nächsten Tokens angesichts der vorherigen Situation wider. Eine höhere Datenkonsistenz führt normalerweise zu einem geringeren Trainingsverlust.
• Durchschnittliche Datenqualität Q: spiegelt die durchschnittliche Qualität der Daten auf Stichprobenebene wider, die anhand verschiedener objektiver und subjektiver Aspekte gemessen werden kann.
• Bei einer bestimmten Menge an Trainingsdaten kann die Modellleistung anhand der oben genannten Faktoren geschätzt werden:
wobei f eine implizite Funktion ist. Bei einem bestimmten Basismodell hängt die Skala von L normalerweise von R und C ab und kann wie folgt ausgedrückt werden:


Da ein Datensatz mit höherer Homogenität oder besserer Datenkonsistenz vom Modell leichter zu erlernen ist, wird L erwartet in R und C monoton sein. Daher können wir die obige Formel wie folgt umschreiben:

wobei g' eine Umkehrfunktion ist. Durch die Kombination der obigen drei Gleichungen erhalten wir:

wobei h eine weitere implizite Funktion ist. Wenn die Datenauswahlmethode die durchschnittliche Datenqualität Q nicht wesentlich verändert, können wir die Variable Q näherungsweise als Konstante behandeln. Daher kann die endgültige Leistung grob ausgedrückt werden als:
Dies bedeutet, dass die Modellleistung mit der Datenkomprimierungsrate und dem Trainingsverlust zusammenhängt. Wir nennen diese Beziehung „Entropiegesetz“.

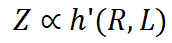
Basierend auf dem Entropiegesetz schlagen wir zwei Schlussfolgerungen vor:


Wenn C als Konstante betrachtet wird, wird der Trainingsverlust direkt von der Kompressionsrate beeinflusst. Daher wird die Modellleistung durch das Komprimierungsverhältnis gesteuert: Wenn das Datenkomprimierungsverhältnis R höher ist, ist Z normalerweise schlechter, was in unseren Experimenten bestätigt wird.
Bei gleichem Komprimierungsverhältnis bedeutet ein höherer Trainingsverlust eine geringere Datenkonsistenz. Daher ist das vom Modell erlernte effektive Wissen möglicherweise begrenzter. Dies kann verwendet werden, um die Leistung von LLM bei verschiedenen Daten mit ähnlichem Komprimierungsverhältnis und ähnlicher Probenqualität vorherzusagen. Die Anwendung dieser Argumentation in der Praxis werden wir später zeigen.


ZIP: Sehr leichter Datenauswahlalgorithmus

Unter der Anleitung des Entropiegesetzes haben wir ZIP vorgeschlagen, eine Datenauswahlmethode, um Datenproben anhand der Datenkomprimierungsrate auszuwählen, mit dem Ziel, die zu maximieren Menge effektiver Informationen bei begrenztem Trainingsdatenbudget. Aus Effizienzgründen verwenden wir ein iteratives mehrstufiges Greedy-Paradigma, um Näherungslösungen mit relativ niedrigen Komprimierungsraten effizient zu erhalten. In jeder Iteration verwenden wir zunächst eine globale Auswahlphase, um einen Pool von Kandidatenproben mit niedrigem Komprimierungsverhältnis auszuwählen, um Proben mit hoher Informationsdichte zu finden. Anschließend verwenden wir eine grobkörnige lokale Auswahlstufe, um einen Satz kleinerer Stichproben auszuwählen, die mit den ausgewählten Stichproben die geringste Redundanz aufweisen. Schließlich verwenden wir eine feinkörnige lokale Auswahlstufe, um die Ähnlichkeit zwischen den hinzuzufügenden Proben zu minimieren. Der obige Prozess wird fortgesetzt, bis genügend Daten vorliegen:



Experimentelle Ergebnisse


1. Wirksamkeit des ZIP-Auswahlalgorithmus für verschiedene LLMs und in verschiedenen LLM-Ausrichtungsphasen

Beim Vergleich verschiedener SFT-Datenauswahlalgorithmen zeigt das auf ZIP-Auswahldaten trainierte Modell Vorteile in der Leistung und ist auch in der Effizienz überlegen. Die spezifischen Ergebnisse sind in der folgenden Tabelle aufgeführt:

Dank der modellunabhängigen und inhaltsunabhängigen Eigenschaften von ZIP kann es auch auf die Datenauswahl in der Präferenzausrichtungsphase angewendet werden. Auch die von ZIP ausgewählten Daten weisen große Vorteile auf. Die spezifischen Ergebnisse sind in der folgenden Tabelle aufgeführt: 2. Experimentelle Überprüfung des Entropiegesetzes des Modells in den vorherigen Trainingsschritten bzw. Es wurden mehrere Beziehungskurven angepasst. Die Ergebnisse sind in den Abbildungen 2 und 3 dargestellt, aus denen wir die enge Korrelation zwischen den drei Faktoren erkennen können. Erstens führen Daten mit niedriger Komprimierungsrate normalerweise zu besseren Modellergebnissen. Dies liegt daran, dass der Lernprozess von LLMs stark mit der Informationskomprimierung zusammenhängt. Wir können uns LLM als Datenkomprimierer vorstellen, sodass Daten mit niedrigerer Komprimierungsrate mehr Daten bedeuten Wissen und damit wertvoller für den Kompressor. Gleichzeitig ist zu beobachten, dass niedrigere Komprimierungsraten in der Regel mit höheren Trainingsverlusten einhergehen. Dies liegt daran, dass Daten, die schwer zu komprimieren sind, mehr Wissen enthalten, was das LLM vor größere Herausforderungen stellt, das darin enthaltene Wissen zu absorbieren.



                                                                               Abbildung 3 Llama-3-8B
Wir stellen ein Entropiegesetz bereit, um die inkrementelle Aktualisierung von LLM-Trainingsdaten in realen Anwendungsszenarien zu steuern. In diesem Aufgabenszenario bleibt die Menge der Trainingsdaten relativ stabil und nur ein kleiner Teil der Daten wird geändert. Die Ergebnisse sind in Abbildung 4 dargestellt, wobei bis ^{fünf Datenversionen sind, die schrittweise inkrementell aktualisiert werden. Aus Gründen der Vertraulichkeit wird nur die relative Beziehung der Modelleffekte bei unterschiedlichen Komprimierungsraten angegeben. Den Vorhersagen des Entropiegesetzes zufolge ist unter der Annahme, dass die Datenqualität nach jeder inkrementellen Aktualisierung nicht wesentlich abnimmt, zu erwarten, dass sich die Modellleistung mit abnehmender Datenkomprimierungsrate verbessert. Diese Vorhersage stimmt mit den Ergebnissen für die Datenversionen} bis in der Abbildung überein. Allerdings zeigt die Datenversion
einen ungewöhnlichen Anstieg des Verlust- und Datenkomprimierungsverhältnisses, was auf die Möglichkeit einer Verschlechterung der Modellleistung aufgrund einer verringerten Konsistenz der Trainingsdaten hinweist. Diese Vorhersage wurde durch die anschließende Bewertung der Modellleistung weiter bestätigt. Daher kann das Entropiegesetz als Leitprinzip für das LLM-Training dienen und das potenzielle Risiko eines Scheiterns des LLM-Trainings vorhersagen, ohne das Modell bis zur Konvergenz auf dem gesamten Datensatz zu trainieren. Dies ist besonders wichtig angesichts der hohen Kosten für die Ausbildung von LLMs.


                                                                       

Das obige ist der detaillierte Inhalt vonDie Universität für Wissenschaft und Technologie Chinas und Huawei Noah haben das Entropiegesetz vorgeschlagen, um den Zusammenhang zwischen der Leistung großer Modelle, der Datenkomprimierungsrate und dem Trainingsverlust aufzudecken.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!