
贝叶斯神经网络模型(Bayesian Neural Networks, BNNs)和概率神经网络模型(Probabilistic Neural Networks, PNNs)是神经网络领域中两种重要的概率模型。它们都处理不确定性,并推断模型参数的后验分布。尽管两者有相似之处,但在方法和理论上存在一些区别。 首先,BNNs使用贝叶斯推断来处理模型参数的不确定性。它们引入先验分布来表示对参数的先验信念,并使用贝叶斯定理更新参数的后验分布。通过引入参数的不确定性,BNNs能够提供对预测的置信度度量,并能够灵活地适应新数据。 相比之下,PNNs使用其他概率模型(如高斯混合模型)来表示模型参数的不确定性。它们通过最大似然估计或期望最大化算法来估计参数,并使用概率分布来表示参数的不确定性。尽管PNNs没有使用贝叶斯推断,但它们仍然能够提供对预
1、理论基础
BNNs是基于贝叶斯统计学的模型,它使用联合概率分布来描述模型参数和数据之间的关系。模型包含一个先验分布,用于表示参数的先验知识,以及一个似然函数,用于表示数据对参数的贡献。在该模型中,参数是随机变量,因此可以推断参数的后验分布。在推断过程中,可以使用贝叶斯定理计算后验分布,从而获得参数的不确定性信息。
PNNs(概率神经网络)是一种基于概率论的模型,旨在充分考虑模型的随机性和不确定性,并能够对模型参数和输出进行概率推断。相比传统神经网络,PNNs不仅能够输出期望值,还能够提供概率分布信息。在PNNs中,模型的输出和参数都被视为随机变量,并可通过概率分布进行描述。这使得PNNs能够更好地处理不确定性和噪声,并作出更可靠的预测或决策。通过引入概率推断,PNNs为各种任务,如分类、回归和生成模型等提供了强大的建模能力。
2、模型表达能力
BNNs:BNNs通常具有更强的模型表达能力,因为它可以通过选择不同的先验分布来表示不同的函数类。在BNNs中,参数的先验分布可以被视为正则化项,因此可以控制模型的复杂度。同时,BNNs还可以通过使用多个分布来表示不同层之间的关系,从而提高模型的表达能力。
PNNs:PNNs的表达能力相对较弱,因为它只能使用一个分布来表示整个模型。在PNNs中,模型的不确定性通常由随机噪声和输入变量的不确定性引起。因此,PNNs通常用于处理具有较高噪声和不确定性的数据集。
3、可解释性
BNNs:BNNs通常具有较高的可解释性,因为它可以提供参数的后验分布,从而可以得到参数的不确定性信息。此外,BNNs还可以通过选择不同的先验分布来表达先验知识,从而提高模型的可解释性。
PNNs:PNNs相对较难解释,因为它通常只能输出概率分布,而不能提供参数的具体值。此外,PNNs的不确定性通常是由随机噪声和输入变量的不确定性引起的,而不是由参数的不确定性引起的。因此,PNNs在解释模型的不确定性时可能会存在一些困难。
4、计算复杂度
BNNs:BNNs通常具有较高的计算复杂度,因为需要进行贝叶斯推断来计算参数的后验分布。此外,BNNs通常需要使用MCMC等高级采样算法来进行推断,这也会增加计算复杂度。
PNNs:PNNs的计算复杂度相对较低,因为它可以使用标准的反向传播算法来进行参数更新和梯度计算。此外,PNNs通常只需要输出概率分布,而不需要计算具体的参数值,因此计算复杂度相对较低。
5、应用领域
BNNs:BNNs通常用于小数据集和需要较高的模型鲁棒性的任务,如医疗和金融领域。此外,BNNs还可以用于不确定性量化和模型选择等任务。
PNNs:PNNs通常用于大规模数据集和需要高度可解释性的任务,如图像生成和自然语言处理。此外,PNNs还可以用于异常检测和模型压缩等任务。
6、关联点:
BNNs和PNNs都是概率神经网络的重要代表,它们都使用了概率编程语言来描述模型和推断过程。
在实践中,PNNs通常使用BNNs作为其基础模型,从而利用贝叶斯方法来进行后验推断。这种方法被称为BNNs的变分推断,可以提高模型的可解释性和泛化性能,并且可以处理大规模数据集。
综合来看,BNNs和PNNs都是在神经网络领域中非常重要的概率模型,它们在理论和方法上有一些不同之处,但也有一些相似之处。BNNs通常具有更强的模型表达能力和可解释性,但计算复杂度相对较高,适用于小数据集和需要较高的模型鲁棒性的任务。PNNs相对较易于计算,适用于大规模数据集和需要高度可解释性的任务。在实践中,PNNs通常使用BNNs作为其基础模型,从而利用贝叶斯方法来进行后验推断。
以上是对比分析贝叶斯神经网络模型与概率神经网络模型的详细内容。更多信息请关注PHP中文网其他相关文章!
 让我们跳舞:结构化运动以微调我们的人类神经网Apr 27, 2025 am 11:09 AM
让我们跳舞:结构化运动以微调我们的人类神经网Apr 27, 2025 am 11:09 AM科学家已经广泛研究了人类和更简单的神经网络(如秀丽隐杆线虫中的神经网络),以了解其功能。 但是,出现了一个关键问题:我们如何使自己的神经网络与新颖的AI一起有效地工作
 新的Google泄漏揭示了双子AI的订阅更改Apr 27, 2025 am 11:08 AM
新的Google泄漏揭示了双子AI的订阅更改Apr 27, 2025 am 11:08 AMGoogle的双子座高级:新的订阅层即将到来 目前,访问Gemini Advanced需要$ 19.99/月Google One AI高级计划。 但是,Android Authority报告暗示了即将发生的变化。 最新的Google P中的代码
 数据分析加速度如何求解AI的隐藏瓶颈Apr 27, 2025 am 11:07 AM
数据分析加速度如何求解AI的隐藏瓶颈Apr 27, 2025 am 11:07 AM尽管围绕高级AI功能炒作,但企业AI部署中潜伏的巨大挑战:数据处理瓶颈。首席执行官庆祝AI的进步时,工程师努力应对缓慢的查询时间,管道超载,一个
 Markitdown MCP可以将任何文档转换为Markdowns!Apr 27, 2025 am 09:47 AM
Markitdown MCP可以将任何文档转换为Markdowns!Apr 27, 2025 am 09:47 AM处理文档不再只是在您的AI项目中打开文件,而是将混乱变成清晰度。诸如PDF,PowerPoints和Word之类的文档以各种形状和大小淹没了我们的工作流程。检索结构化
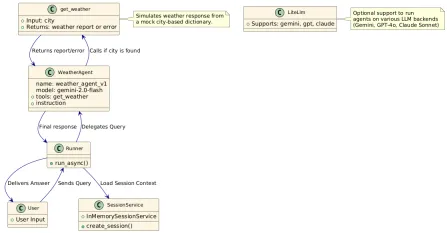 如何使用Google ADK进行建筑代理? - 分析VidhyaApr 27, 2025 am 09:42 AM
如何使用Google ADK进行建筑代理? - 分析VidhyaApr 27, 2025 am 09:42 AM利用Google的代理开发套件(ADK)的力量创建具有现实世界功能的智能代理!该教程通过使用ADK来构建对话代理,并支持Gemini和GPT等各种语言模型。 w
 在LLM上使用SLM进行有效解决问题-Analytics VidhyaApr 27, 2025 am 09:27 AM
在LLM上使用SLM进行有效解决问题-Analytics VidhyaApr 27, 2025 am 09:27 AM摘要: 小型语言模型 (SLM) 专为效率而设计。在资源匮乏、实时性和隐私敏感的环境中,它们比大型语言模型 (LLM) 更胜一筹。 最适合专注型任务,尤其是在领域特异性、控制性和可解释性比通用知识或创造力更重要的情况下。 SLM 并非 LLMs 的替代品,但在精度、速度和成本效益至关重要时,它们是理想之选。 技术帮助我们用更少的资源取得更多成就。它一直是推动者,而非驱动者。从蒸汽机时代到互联网泡沫时期,技术的威力在于它帮助我们解决问题的程度。人工智能 (AI) 以及最近的生成式 AI 也不例
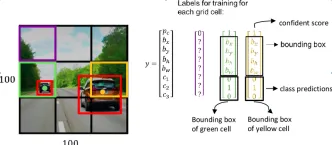 如何将Google Gemini模型用于计算机视觉任务? - 分析VidhyaApr 27, 2025 am 09:26 AM
如何将Google Gemini模型用于计算机视觉任务? - 分析VidhyaApr 27, 2025 am 09:26 AM利用Google双子座的力量用于计算机视觉:综合指南 领先的AI聊天机器人Google Gemini扩展了其功能,超越了对话,以涵盖强大的计算机视觉功能。 本指南详细说明了如何利用
 Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好吗?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好吗?Apr 27, 2025 am 09:20 AM2025年的AI景观正在充满活力,而Google的Gemini 2.0 Flash和Openai的O4-Mini的到来。 这些尖端的车型分开了几周,具有可比的高级功能和令人印象深刻的基准分数。这个深入的比较


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

PhpStorm Mac 版本
最新(2018.2.1 )专业的PHP集成开发工具

ZendStudio 13.5.1 Mac
功能强大的PHP集成开发环境

DVWA
Damn Vulnerable Web App (DVWA) 是一个PHP/MySQL的Web应用程序,非常容易受到攻击。它的主要目标是成为安全专业人员在合法环境中测试自己的技能和工具的辅助工具,帮助Web开发人员更好地理解保护Web应用程序的过程,并帮助教师/学生在课堂环境中教授/学习Web应用程序安全。DVWA的目标是通过简单直接的界面练习一些最常见的Web漏洞,难度各不相同。请注意,该软件中

Atom编辑器mac版下载
最流行的的开源编辑器

记事本++7.3.1
好用且免费的代码编辑器





