
线性支持向量机(LSVM)和一般支持向量机(SVM)是常用于分类和回归的机器学习模型。它们的核心思想是通过在数据空间中找到最佳超平面来分离不同的类别或解决回归问题。尽管它们都属于支持向量机的范畴,但它们之间存在一些区别。 LSVM是一种基于线性核函数的支持向量机模型,它假设数据可以通过一个线性超平面进行良好的分割。它的优点是计算简单且容易解释,但它只能处理线性可分问题,对于非线性数据可能效果不佳。 SVM是一种更通用的支持向量机模型,它使用核函数来将数据映射到高维特征空间,从而将非线性问题转化为线性可分问题。SVM可以使用不同的核函数来适应不同类型的数据,例如多项式核、高斯核等。这使得SVM在处理非线性问题时表现更好,但计算复杂度相对
1.模型形式
LSVM是一种线性分类器,其决策边界为一个超平面,表示为w^Tx+b=0。其中,w是法向量,b是偏移量。与LSVM不同,SVM不仅支持线性分类,还能使用核函数将数据映射到高维空间中进行非线性分类或回归。SVM的决策边界可表示为sum_{i=1}^nalpha_i y_i K(x_i,x)+b=0。在此方程中,alpha_i是拉格朗日乘子,y_i是标签,K(x_i,x)是核函数的输出。
2.模型优化
LSVM和SVM在模型优化上有一些不同。LSVM的目标是最大化间隔,即使得决策边界到每个类别最近样本点的距离最大化。而SVM的目标是同时最小化损失函数并最大化间隔。SVM通常使用Hinge Loss作为损失函数,它能惩罚误分类的样本。
3.解决问题类型
LSVM仅能进行线性分类或回归,对于非线性问题需要使用非线性变换或者核函数来进行处理。而SVM不仅可以处理线性问题,还可以使用核函数将数据映射到更高维的空间中进行非线性分类或回归。这也是SVM相比LSVM更加灵活的原因之一。
4.模型复杂度
由于SVM支持使用核函数进行非线性分类或回归,因此其模型复杂度一般比LSVM更高。在使用核函数时,数据被映射到高维空间中,导致模型需要处理更多的特征。这也导致SVM的训练时间和计算资源消耗更高,对于大规模数据集的处理可能会带来挑战。
5.对异常值的鲁棒性
LSVM对异常值比较敏感,因为它的目标是最大化间隔,而异常值可能会对间隔产生较大的影响。而SVM则相对鲁棒一些,它使用了Hinge Loss来对误分类样本进行惩罚,因此对于一些异常值的影响会相对较小。
总的来说,LSVM和SVM都是支持向量机的变种,都能够用于分类和回归问题。相比LSVM,SVM更加灵活,可以处理非线性问题,并且相对鲁棒一些。但是,SVM的模型复杂度更高,需要更多的计算资源和训练时间。因此,在实际应用中需要根据具体情况选择适合的模型。
以上是线性支持向量机和一般向量机的区别的详细内容。更多信息请关注PHP中文网其他相关文章!
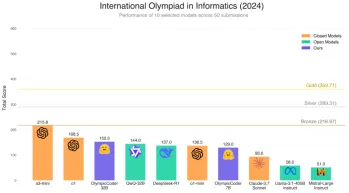 拥抱面部是否7B型号奥林匹克赛车击败克劳德3.7?Apr 23, 2025 am 11:49 AM
拥抱面部是否7B型号奥林匹克赛车击败克劳德3.7?Apr 23, 2025 am 11:49 AM拥抱Face的OlympicCoder-7B:强大的开源代码推理模型 开发以代码为中心的语言模型的竞赛正在加剧,拥抱面孔与强大的竞争者一起参加了比赛:OlympicCoder-7B,一种产品
 4个新的双子座功能您可以错过Apr 23, 2025 am 11:48 AM
4个新的双子座功能您可以错过Apr 23, 2025 am 11:48 AM你们当中有多少人希望AI可以做更多的事情,而不仅仅是回答问题?我知道我有,最近,我对它的变化感到惊讶。 AI聊天机器人不仅要聊天,还关心创建,研究
 Camunda为经纪人AI编排编写了新的分数Apr 23, 2025 am 11:46 AM
Camunda为经纪人AI编排编写了新的分数Apr 23, 2025 am 11:46 AM随着智能AI开始融入企业软件平台和应用程序的各个层面(我们必须强调的是,既有强大的核心工具,也有一些不太可靠的模拟工具),我们需要一套新的基础设施能力来管理这些智能体。 总部位于德国柏林的流程编排公司Camunda认为,它可以帮助智能AI发挥其应有的作用,并与新的数字工作场所中的准确业务目标和规则保持一致。该公司目前提供智能编排功能,旨在帮助组织建模、部署和管理AI智能体。 从实际的软件工程角度来看,这意味着什么? 确定性与非确定性流程的融合 该公司表示,关键在于允许用户(通常是数据科学家、软件
 策划的企业AI体验是否有价值?Apr 23, 2025 am 11:45 AM
策划的企业AI体验是否有价值?Apr 23, 2025 am 11:45 AM参加Google Cloud Next '25,我渴望看到Google如何区分其AI产品。 有关代理空间(此处讨论)和客户体验套件(此处讨论)的最新公告很有希望,强调了商业价值
 如何为抹布找到最佳的多语言嵌入模型?Apr 23, 2025 am 11:44 AM
如何为抹布找到最佳的多语言嵌入模型?Apr 23, 2025 am 11:44 AM为您的检索增强发电(RAG)系统选择最佳的多语言嵌入模型 在当今的相互联系的世界中,建立有效的多语言AI系统至关重要。 强大的多语言嵌入模型对于RE至关重要
 麝香:奥斯汀的机器人需要每10,000英里进行干预Apr 23, 2025 am 11:42 AM
麝香:奥斯汀的机器人需要每10,000英里进行干预Apr 23, 2025 am 11:42 AM特斯拉的Austin Robotaxi发射:仔细观察Musk的主张 埃隆·马斯克(Elon Musk)最近宣布,特斯拉即将在德克萨斯州奥斯汀推出的Robotaxi发射,最初出于安全原因部署了一支小型10-20辆汽车,并有快速扩张的计划。 h
 AI震惊的枢轴:从工作工具到数字治疗师和生活教练Apr 23, 2025 am 11:41 AM
AI震惊的枢轴:从工作工具到数字治疗师和生活教练Apr 23, 2025 am 11:41 AM人工智能的应用方式可能出乎意料。最初,我们很多人可能认为它主要用于代劳创意和技术任务,例如编写代码和创作内容。 然而,哈佛商业评论最近报道的一项调查表明情况并非如此。大多数用户寻求人工智能的并非是代劳工作,而是支持、组织,甚至是友谊! 报告称,人工智能应用案例的首位是治疗和陪伴。这表明其全天候可用性以及提供匿名、诚实建议和反馈的能力非常有价值。 另一方面,营销任务(例如撰写博客、创建社交媒体帖子或广告文案)在流行用途列表中的排名要低得多。 这是为什么呢?让我们看看研究结果及其对我们人类如何继续将


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

EditPlus 中文破解版
体积小,语法高亮,不支持代码提示功能

ZendStudio 13.5.1 Mac
功能强大的PHP集成开发环境

DVWA
Damn Vulnerable Web App (DVWA) 是一个PHP/MySQL的Web应用程序,非常容易受到攻击。它的主要目标是成为安全专业人员在合法环境中测试自己的技能和工具的辅助工具,帮助Web开发人员更好地理解保护Web应用程序的过程,并帮助教师/学生在课堂环境中教授/学习Web应用程序安全。DVWA的目标是通过简单直接的界面练习一些最常见的Web漏洞,难度各不相同。请注意,该软件中

螳螂BT
Mantis是一个易于部署的基于Web的缺陷跟踪工具,用于帮助产品缺陷跟踪。它需要PHP、MySQL和一个Web服务器。请查看我们的演示和托管服务。

mPDF
mPDF是一个PHP库,可以从UTF-8编码的HTML生成PDF文件。原作者Ian Back编写mPDF以从他的网站上“即时”输出PDF文件,并处理不同的语言。与原始脚本如HTML2FPDF相比,它的速度较慢,并且在使用Unicode字体时生成的文件较大,但支持CSS样式等,并进行了大量增强。支持几乎所有语言,包括RTL(阿拉伯语和希伯来语)和CJK(中日韩)。支持嵌套的块级元素(如P、DIV),






