
在机器学习中,相似矩阵是一种数学工具,用于衡量数据之间的相似性。它通常由一个n x n的矩阵表示,其中n是数据集中的样本数。相似矩阵的元素可以表示两个数据之间的相似度或距离。通过分析相似矩阵,我们可以识别出数据之间的模式和关联,进而进行分类、聚类等任务。相似矩阵在机器学习算法中具有广泛的应用,例如推荐系统、图像识别等领域。
相似矩阵可以通过多种方法计算得到,如欧几里得距离、余弦相似度和相关系数等。其中,欧几里得距离是常用的计算相似矩阵的方法之一,用于计算两个向量间的距离。余弦相似度则衡量两个向量夹角的余弦值,表示它们的相似程度。这些方法都可以应用于不同领域的数据分析和模式识别任务中,根据具体情况选择适合的方法来计算相似矩阵。
相似矩阵在机器学习中有广泛应用,包括聚类、降维、分类和推荐系统等领域。在聚类中,相似矩阵用于计算数据点之间的相似度,进而将它们分配到不同的簇中。在降维中,相似矩阵用于计算数据点之间的相似度,以将高维数据映射到低维空间中。而在分类和推荐系统中,相似矩阵可用于计算不同数据点之间的相似度,从而实现分类和推荐任务。相似矩阵的应用帮助机器学习算法更好地理解数据之间的关系,进而提高模型的性能和准确度。
相似矩阵在机器学习中是重要概念,用于描述数据相似性,实现不同的学习任务。
相似矩阵在机器学习领域有着多种应用,具体如下:
1.特征降维
通过计算数据集的协方差矩阵,可以得到一个实对称矩阵,进而通过特征值分解得到特征向量。这些特征向量可以被用来构建相似矩阵,从而实现数据降维。
2.图像处理
在图像处理中,可以通过计算两幅图像的相似矩阵来比较它们的相似度,从而实现图像匹配和识别等任务。
3.谱聚类
谱聚类是一种基于相似矩阵的聚类方法,它通过计算数据集的相似矩阵来实现对数据的聚类。相似矩阵中的元素可以表示数据点之间的相似度,从而将数据点聚集到同一个类别中。
4.矩阵分解
在矩阵分解中,可以通过计算两个矩阵的相似矩阵来比较它们之间的相似度,从而实现矩阵的分解和重构。
总的来说,相似矩阵在机器学习中被广泛应用于数据降维、图像处理、聚类和矩阵分解等领域。
以上是矩阵相似性的定义及其实际应用的详细内容。更多信息请关注PHP中文网其他相关文章!
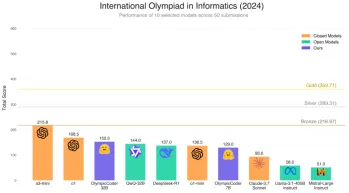 拥抱面部是否7B型号奥林匹克赛车击败克劳德3.7?Apr 23, 2025 am 11:49 AM
拥抱面部是否7B型号奥林匹克赛车击败克劳德3.7?Apr 23, 2025 am 11:49 AM拥抱Face的OlympicCoder-7B:强大的开源代码推理模型 开发以代码为中心的语言模型的竞赛正在加剧,拥抱面孔与强大的竞争者一起参加了比赛:OlympicCoder-7B,一种产品
 4个新的双子座功能您可以错过Apr 23, 2025 am 11:48 AM
4个新的双子座功能您可以错过Apr 23, 2025 am 11:48 AM你们当中有多少人希望AI可以做更多的事情,而不仅仅是回答问题?我知道我有,最近,我对它的变化感到惊讶。 AI聊天机器人不仅要聊天,还关心创建,研究
 Camunda为经纪人AI编排编写了新的分数Apr 23, 2025 am 11:46 AM
Camunda为经纪人AI编排编写了新的分数Apr 23, 2025 am 11:46 AM随着智能AI开始融入企业软件平台和应用程序的各个层面(我们必须强调的是,既有强大的核心工具,也有一些不太可靠的模拟工具),我们需要一套新的基础设施能力来管理这些智能体。 总部位于德国柏林的流程编排公司Camunda认为,它可以帮助智能AI发挥其应有的作用,并与新的数字工作场所中的准确业务目标和规则保持一致。该公司目前提供智能编排功能,旨在帮助组织建模、部署和管理AI智能体。 从实际的软件工程角度来看,这意味着什么? 确定性与非确定性流程的融合 该公司表示,关键在于允许用户(通常是数据科学家、软件
 策划的企业AI体验是否有价值?Apr 23, 2025 am 11:45 AM
策划的企业AI体验是否有价值?Apr 23, 2025 am 11:45 AM参加Google Cloud Next '25,我渴望看到Google如何区分其AI产品。 有关代理空间(此处讨论)和客户体验套件(此处讨论)的最新公告很有希望,强调了商业价值
 如何为抹布找到最佳的多语言嵌入模型?Apr 23, 2025 am 11:44 AM
如何为抹布找到最佳的多语言嵌入模型?Apr 23, 2025 am 11:44 AM为您的检索增强发电(RAG)系统选择最佳的多语言嵌入模型 在当今的相互联系的世界中,建立有效的多语言AI系统至关重要。 强大的多语言嵌入模型对于RE至关重要
 麝香:奥斯汀的机器人需要每10,000英里进行干预Apr 23, 2025 am 11:42 AM
麝香:奥斯汀的机器人需要每10,000英里进行干预Apr 23, 2025 am 11:42 AM特斯拉的Austin Robotaxi发射:仔细观察Musk的主张 埃隆·马斯克(Elon Musk)最近宣布,特斯拉即将在德克萨斯州奥斯汀推出的Robotaxi发射,最初出于安全原因部署了一支小型10-20辆汽车,并有快速扩张的计划。 h
 AI震惊的枢轴:从工作工具到数字治疗师和生活教练Apr 23, 2025 am 11:41 AM
AI震惊的枢轴:从工作工具到数字治疗师和生活教练Apr 23, 2025 am 11:41 AM人工智能的应用方式可能出乎意料。最初,我们很多人可能认为它主要用于代劳创意和技术任务,例如编写代码和创作内容。 然而,哈佛商业评论最近报道的一项调查表明情况并非如此。大多数用户寻求人工智能的并非是代劳工作,而是支持、组织,甚至是友谊! 报告称,人工智能应用案例的首位是治疗和陪伴。这表明其全天候可用性以及提供匿名、诚实建议和反馈的能力非常有价值。 另一方面,营销任务(例如撰写博客、创建社交媒体帖子或广告文案)在流行用途列表中的排名要低得多。 这是为什么呢?让我们看看研究结果及其对我们人类如何继续将


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

SublimeText3 英文版
推荐:为Win版本,支持代码提示!

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

mPDF
mPDF是一个PHP库,可以从UTF-8编码的HTML生成PDF文件。原作者Ian Back编写mPDF以从他的网站上“即时”输出PDF文件,并处理不同的语言。与原始脚本如HTML2FPDF相比,它的速度较慢,并且在使用Unicode字体时生成的文件较大,但支持CSS样式等,并进行了大量增强。支持几乎所有语言,包括RTL(阿拉伯语和希伯来语)和CJK(中日韩)。支持嵌套的块级元素(如P、DIV),

禅工作室 13.0.1
功能强大的PHP集成开发环境






