
在机器学习领域,扩散模型在图像处理中起到了广泛的作用。它被应用在多个图像处理任务上,包括图像去噪、图像增强以及图像分割等。扩散模型的主要优势在于它能够有效处理图像中的噪声,同时还能增强图像的细节和对比度,并且能够对图像进行准确的分割。此外,扩散模型还具有高计算效率和易于实现的特点。总之,扩散模型在图像处理中发挥着重要的作用,为我们提供了一种强大的工具来改善图像质量和提取图像特征。
扩散模型在图像处理中的作用
扩散模型是一种基于偏微分方程的机器学习模型,主要应用于图像处理领域。其基本原理是模拟物理扩散过程,通过控制偏微分方程的参数来实现图像的去噪、增强和分割等处理操作。 这一模型最早由Perona和Malik于1990年提出,其核心思想是通过调整偏微分方程的参数,逐渐平滑或扩散图像中的信息。具体而言,扩散模型通过将图像中的像素与其邻域像素之间的差异进行比较,并根据差异的大小来调整像素的强度值。这样做可以减少图像中的噪声,并增强图像的细节。 扩散模型在图像处理中有广泛的应用。例如,在图像去噪方面,它可以有效地去除图像中的噪声,使图像更清晰。在图像增强方面,它可以增强图像的对比度和细节,使图像更加鲜明。在图像分割
具体而言,扩散模型在图像处理中的作用如下:
1.图像去噪
扩散模型可以通过模拟噪声的扩散过程,将噪声逐渐平滑,从而实现图像去噪。具体来说,扩散模型可以使用偏微分方程描述噪声在图像中的扩散过程,并通过反复迭代求解微分方程来平滑噪声。这种方法可以有效地去除高斯噪声、椒盐噪声等常见的图像噪声。
2.图像增强
扩散模型可以通过增加图像的细节和对比度,实现图像增强。具体来说,扩散模型可以使用偏微分方程描述图像中颜色或强度的扩散过程,并通过控制扩散系数、时间步长等参数来增加图像的细节和对比度。这种方法可以有效地增强图像的纹理、边缘等细节,使图像更加清晰、鲜明。
3.图像分割
扩散模型可以通过模拟边缘的扩散过程,实现图像分割。具体来说,扩散模型可以使用偏微分方程描述图像中灰度值的扩散过程,并通过控制扩散系数、时间步长等参数来实现图像的分割。这种方法可以有效地分割出图像中的不同物体或区域,为后续的图像分析和处理提供基础。
扩散模型在生成图像时为什么能生成细节
扩散模型使用偏微分方程描述颜色或强度在空间和时间上的演化,通过反复迭代求解微分方程,得到图像的最终状态。扩散模型能够生成细节的原因有以下几点:
1.模拟物理过程
扩散模型的基本原理是模拟物理过程,即颜色或强度的扩散。在这种过程中,每个像素点的值都受到其周围像素的影响,因此在迭代求解微分方程时,每个像素点都会被更新多次。这种迭代过程能够反复强化像素点之间的相互作用,从而生成更加细致的图像。
2.控制参数
扩散模型中有许多控制参数,如扩散系数、时间步长等,这些参数能够影响图像的生成过程。通过调整这些参数,可以控制图像的生成方向和细节程度。例如,增加扩散系数可以使颜色或强度更快地扩散,从而生成更加模糊的图像;减小时间步长可以增加迭代次数,从而生成更加细致的图像。
3.随机性
扩散模型中还有一些随机性的因素,如初始值、噪声等,这些因素能够增加图像的变化和细节。例如,在初始值中加入一些噪声,可以使图像生成的过程更加随机,从而生成更加细致的图像;在迭代过程中,也可以加入一些随机扰动,以增加图像的变化和细节。
4.多尺度处理
扩散模型可以通过多尺度处理来增加图像的细节。具体来说,可以先将原始图像进行下采样,生成一个较小的图像,然后在这个较小的图像上进行扩散模型的求解。这样做的好处是可以使图像的细节更加突出,同时也能够提高模型的计算效率。
5.结合其他模型
扩散模型可以和其他模型结合使用,从而进一步增加图像的细节。例如,可以将扩散模型和生成对抗网络(GAN)结合使用,用GAN生成的图像作为扩散模型的初始图像,然后在此基础上通过扩散模型进一步增加细节,生成更加逼真的图像。
扩散模型的数学基础
扩散模型的数学基础是偏微分方程,其基本形式为:
∂u/∂t=div(c(∇u)),其中u(x,y,t)表示在时间t的位置(x,y)处的图像灰度值,c(∇u)表示扩散系数,div表示散度算子,∇表示梯度算子。
这个方程描述了一个灰度图像中灰度值的扩散过程,其中c(∇u)控制了扩散的方向和速度。通常情况下,c(∇u)是一个非线性函数,它可以根据图像的特征进行调整,从而达到不同的图像处理效果。例如,当c(∇u)为高斯函数时,扩散模型可以用来去除高斯噪声;当c(∇u)为梯度函数时,扩散模型可以用来增强图像的边缘特征。
扩散模型的求解过程通常采用迭代方法,即在每一步中通过求解偏微分方程来更新图像的灰度值。对于二维图像,扩散模型可以在x和y两个方向上进行迭代。在迭代过程中,还可以对扩散系数、时间步长等参数进行调整,以实现不同的图像处理效果。
扩散模型损失下降的很快的原因
在扩散模型中,损失函数的下降速度往往非常快,这是由于扩散模型本身的特点所致。
在机器学习中,扩散模型的应用主要是对图像进行去噪或者边缘检测等处理。这些处理通常可以转化为一个求解偏微分方程的优化问题,即最小化损失函数。
在扩散模型中,损失函数通常定义为原始图像和处理后图像之间的差异。因此,优化损失函数的过程就是通过调整模型参数,使得处理后图像尽可能接近原始图像的过程。由于扩散模型的数学表达式比较简单,而且其模型参数通常较少,所以在训练过程中损失函数的下降速度往往非常快。
另外,扩散模型的损失函数通常是凸函数,这意味着在训练过程中,损失函数的下降速度不会出现明显的震荡现象,而是呈现出平滑的下降趋势。这也是损失函数下降速度快的原因之一。
除了上述原因之外,扩散模型的损失函数下降速度快还与其模型结构和优化算法有关。扩散模型通常采用隐式数值方法求解偏微分方程,这种方法具有较高的计算效率和数值稳定性,可以有效地解决数值求解过程中的数值误差和耗时问题。此外,扩散模型的优化算法通常采用梯度下降等优化算法,这些算法在处理高维数据时可以有效地降低计算复杂度,从而加快损失函数的下降速度。
扩散模型的损失函数下降速度快还与其模型的性质和参数选择有关。在扩散模型中,模型的参数通常被设置为常数或者与时间有关的函数,这些参数的选择可以影响模型的性能和损失函数的下降速度。一般来说,设置合适的参数能够加速模型的训练和提高模型的性能。
此外,在扩散模型中,还存在一些优化技巧,可以进一步加快损失函数的下降速度。例如,采用自适应步长的优化算法可以根据损失函数的变化情况自动调整模型参数的更新步长,从而加快模型的收敛速度。此外,采用批量归一化、残差连接等技巧也可以有效地提高模型的训练速度和性能。
扩散模型和神经网络
在机器学习中,扩散模型主要应用于图像处理和计算机视觉领域。例如,可以利用扩散模型对图像进行去噪或者边缘检测等处理。此外,扩散模型还可以用于图像分割、目标识别等领域。扩散模型的优点是可以处理高维数据,具有较强的抗噪性和平滑性,但是其计算效率较低,需要大量的计算资源和时间。
神经网络在机器学习中应用广泛,可以用于图像识别、自然语言处理、语音识别等领域。相比于扩散模型,神经网络具有更强的表达能力和泛化能力,可以处理各种类型的数据,并且可以自动学习特征。但是神经网络的参数数量较大,需要大量的数据和计算资源进行训练,同时其模型结构较为复杂,需要一定的技术和经验才能进行设计和优化。
实际应用中,扩散模型和神经网络常常被结合使用,以充分发挥它们各自的优点。例如,在图像处理中,可以先利用扩散模型对图像进行去噪和平滑处理,然后再将处理后的图像输入到神经网络中进行特征提取和分类识别。这种组合可以提高模型的准确率和鲁棒性,同时也可以加速模型的训练和推理过程。
以上是解析图像处理中的扩散模型应用的详细内容。更多信息请关注PHP中文网其他相关文章!
 用Ollama -Analytics Vidhya简化本地LLM部署Apr 19, 2025 am 11:01 AM
用Ollama -Analytics Vidhya简化本地LLM部署Apr 19, 2025 am 11:01 AM利用Ollama本地开源LLMS的力量:综合指南 运行大型语言模型(LLMS)本地提供无与伦比的控制和透明度,但是设置环境可能令人生畏。 Ollama简化了这个过程
 如何使用Monsterapi微调大语言模型Apr 19, 2025 am 10:49 AM
如何使用Monsterapi微调大语言模型Apr 19, 2025 am 10:49 AM利用微调LLM的功能与Monsterapi:综合指南 想象一个虚拟助手完美理解并预测您的需求。 由于大型语言模型(LLMS)的进步,这已成为现实。 但是,
 5统计测试每个数据科学家都应该知道-Analytics VidhyaApr 19, 2025 am 10:27 AM
5统计测试每个数据科学家都应该知道-Analytics VidhyaApr 19, 2025 am 10:27 AM数据科学的基本统计测试:综合指南 从数据中解锁有价值的见解至关重要。 掌握统计测试对于实现这一目标至关重要。这些测试使数据科学家能够严格瓦尔
 如何使用Florence -2 -Analytics Vidhya执行计算机视觉任务Apr 19, 2025 am 10:21 AM
如何使用Florence -2 -Analytics Vidhya执行计算机视觉任务Apr 19, 2025 am 10:21 AM介绍 原始变压器的引入为当前的大语言模型铺平了道路。同样,在引入变压器模型之后,引入了视觉变压器(VIT)。喜欢
 使用Langchain Text Splitters -Analytics Vidhya拆分数据的7种方法Apr 19, 2025 am 10:11 AM
使用Langchain Text Splitters -Analytics Vidhya拆分数据的7种方法Apr 19, 2025 am 10:11 AMLangchain文本拆分器:优化LLM输入以提高效率和准确性 我们上一篇文章介绍了Langchain的文档加载程序。 但是,LLM具有上下文窗口大小的限制(以代币测量)。 超过此限制会截断数据,comp
 免费生成的AI课程:开创创新的未来Apr 19, 2025 am 10:01 AM
免费生成的AI课程:开创创新的未来Apr 19, 2025 am 10:01 AM生成的AI:革命性的创造力和创新 生成的AI通过按下按钮来创建文本,图像,音乐和虚拟世界来改变行业。 它的影响跨越视频编辑,音乐制作,艺术,娱乐,HEA
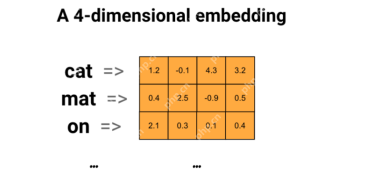 使用通用句子编码器和Wikiqa创建QA模型Apr 19, 2025 am 10:00 AM
使用通用句子编码器和Wikiqa创建QA模型Apr 19, 2025 am 10:00 AM利用嵌入模型的力量来回答高级问题 在当今信息丰富的世界中,立即获得精确答案的能力至关重要。 本文展示了使用强大的提问(QA)模型
 前十名必须阅读机器学习研究论文Apr 19, 2025 am 09:53 AM
前十名必须阅读机器学习研究论文Apr 19, 2025 am 09:53 AM本文探讨了十个彻底改变人工智能(AI)和机器学习(ML)的开创性出版物。 我们将研究神经网络和算法的最新突破,并解释驱动现代AI的核心概念。 Th


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

Dreamweaver Mac版
视觉化网页开发工具

记事本++7.3.1
好用且免费的代码编辑器

mPDF
mPDF是一个PHP库,可以从UTF-8编码的HTML生成PDF文件。原作者Ian Back编写mPDF以从他的网站上“即时”输出PDF文件,并处理不同的语言。与原始脚本如HTML2FPDF相比,它的速度较慢,并且在使用Unicode字体时生成的文件较大,但支持CSS样式等,并进行了大量增强。支持几乎所有语言,包括RTL(阿拉伯语和希伯来语)和CJK(中日韩)。支持嵌套的块级元素(如P、DIV),

安全考试浏览器
Safe Exam Browser是一个安全的浏览器环境,用于安全地进行在线考试。该软件将任何计算机变成一个安全的工作站。它控制对任何实用工具的访问,并防止学生使用未经授权的资源。

适用于 Eclipse 的 SAP NetWeaver 服务器适配器
将Eclipse与SAP NetWeaver应用服务器集成。






