计算幂次k次的幂次%m

我们的目标是计算 k 乘以 % m 的幂，以基数、k 和 m 的值作为输入 -

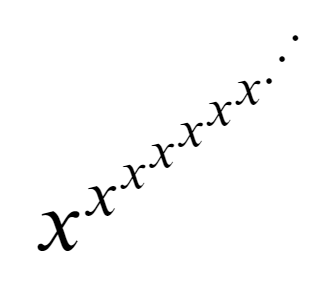
看上面的图片。您是否尝试过计算这样的问题？我们来试试吧。

计算幂的k次方，然后对m取模。

Explanation

的中文翻译为：

解释

在这个问题中，给定了x、k和m。计算${x^{x{^x{^{^.{^{^.{^{^.}}}}}}}}}$，重复k次，然后对m取模。

让我们通过一个例子来理解。

已知，x = 2、k = 4、m = 6

因此，计算 $2^{2^{2{^2}}}:=:4^{2{^2}}:=:16^2:=:256$ p>

然后 256% 6 = 4。

所以，最终结果是4。

方法

让我们讨论一下计算 k 乘以 % m 的幂的分步算法。

• 将x、k和m的值作为输入。

• 使用pow函数计算幂的幂，最后使用取模运算符得到最终结果。

• 将最终结果作为输出打印。

C++程序计算幂的k次方%m。

#include <iostream>
#include <cmath>
using namespace std;

int powofpow(int x, int k){
   int val = x;
   k--;
   while (k--)
      val = pow(val, x);
 
   return val;
}

int main(){
   int x = 5, k = 2, m = 3;
   int result;
   
   result =  powofpow(x, k);
   result %= m;
   
   cout << "Compute power of power " << k << " times % " << m << " of " << x << " is " << result << endl;
   
   return 0;
}

输出

Compute power of power 2 times % 3 of 5 is 2

复杂性

时间复杂度：O(k)，因为此代码执行迭代 (k-1) 次。

空间复杂度：O(1)，因为代码使用固定数量的变量来存储输入值和结果，而不管输入的大小。

结论

在本文中，我们试图解释计算将底数的幂次方k次取模m的方法，其中底数、k和m的值作为输入给出。我希望本文能帮助您更好地理解这个概念。

以上是计算幂次k次的幂次%m的详细内容。更多信息请关注PHP中文网其他相关文章！