尽管 DNN 在各种实际应用中取得了广泛的成功,但其过程通常被视为黑盒子,因为我们很难解释 DNN 如何做出决定。缺乏可解释性损害了 DNN 的可靠性,从而阻碍了它们在高风险任务中的广泛应用,例如自动驾驶和 AI 医疗。因此,可解释 DNN 引起了越来越多的关注。
作为解释 DNN 的典型视角,归因方法旨在计算每个输入变量对网络输出的归因 / 重要性 / 贡献分数。例如,给定一个用于图像分类的预训练 DNN 和一个输入图像,每个输入变量的属性得分是指每个像素对分类置信度得分的数值影响。
尽管近年来研究者提出了许多归因方法,但其中大多数都建立在不同的启发式方法之上。目前还缺乏统一的理论视角来检验这些归因方法的正确性,或者至少在数学上阐明其核心机制。
研究人员曾试图统一不同的归因方法,但这些研究只涵盖了几种方法。
本文中,我们提出了「统一解释 14 种输入单元重要性归因算法的内在机理」。

论文地址:https://arxiv.org/pdf/2303.01506.pdf
其实无论是「12 种提升对抗迁移性的算法」,还是「14 种输入单元重要性归因算法」,都是工程性算法的重灾区。在这两大领域内,大部分算法都是经验性的,人们根据实验经验或直觉认识,设计出一些似是而非的工程性算法。大部分研究没有对 “究竟什么是输入单元重要性” 做出严谨定义和理论论证,少数研究有一定的论证,但往往也很不完善。当然,“缺少严谨的定义和论证” 的问题充满了整个人工智能领域,只是在这两个方向上格外突出。
- 第一,在众多经验性归因算法充斥可解释机器学习领域的环境下,我们希望证明 “所有 14 种归因算法(解释神经网络输入单元重要性的算法)的内在机理,都可以表示为对神经网络所建模的交互效用的一种分配,不同归因算法对应不同的交互效用分配比例”。这样,虽然不同算法有着完全不同的设计着眼点(比如有些算法有提纲挈领的目标函数,有些算法则是纯粹的 pipeline),但是我们发现在数学上,这些算法都可以被我们纳入到 “对交互效用的分配” 的叙事逻辑中来。
- 基于上面的交互效用分配框架,我们可以进一步为神经网络输入单元重要性归因算法提出三条评估准则,来衡量归因算法所预测的输入单元重要性值是否合理。
当然,我们的理论分析不只适用于 14 种归因算法,理论上可以统一更多的类似研究。因为人力有限,这篇论文里我们仅仅讨论 14 种算法。
研究的真正难点在于,不同的经验性归因算法往往都是搭建在不同的直觉之上的,每篇论文都仅仅努力从各自的角度「自圆其说」,分别基于不同的直觉或角度来设计归因算法,而缺少一套规范的数学语言来统一描述各种算法的本质。
算法回顾
在讲数学以前,本文先从直觉层面简单回顾之前的算法。
1. 基于梯度的归因算法。这一类算法普遍认为,神经网络的输出对每个输入单元的梯度可以反映输入单元的重要性。例如,Gradient*Input 算法将输入单元的重要性建模为梯度与输入单元值的逐元素乘积。考虑到梯度仅能反映输入单元的局部重要性,Smooth Gradients 和 Integrated Gradients 算法将重要性建模为平均梯度与输入单元值的逐元素乘积,其中这两种方法中的平均梯度分别指输入样本邻域内梯度的平均值或输入样本到基准点(baseline point)间线性插值点的梯度平均值。类似地,Grad-CAM 算法采用网络输出对每个 channel 中所有特征梯度的平均值,来计算重要性分数。进一步,Expected Gradients 算法认为,选择单个基准点往往会导致有偏的归因结果,从而提出将重要性建模为不同基准点下 Integrated Gradients 归因结果的期望。
2. 基于逐层反向传播的归因算法。深度神经网络往往极为复杂,而每一层神经网络的结构相对简单(比如深层特征通常是浅层特征的线性加和 + 非线性激活函数),便于分析浅层特征对深层特征的重要性。因此,这类算法通过估计中层特征的重要性,并将这些重要性逐层传播直至输入层,得到输入单元的重要性。这一类算法包括 LRP-epsilon, LRP-alphabeta, Deep Taylor, DeepLIFT Rescale, DeepLIFT RevealCancel, DeepShap 等。不同反向传播算法间的根本区别在于,他们采用了不同的重要性逐层传播规则。
3. 基于遮挡的归因算法。这类算法根据遮挡某一输入单元对模型输出的影响,来推断该输入单元的重要性。例如,Occlusion-1(Occlusion-patch)算法将第 i 个像素(像素块)的重要性建模为其它像素未被遮挡时,像素 i 未遮挡和遮挡两种情况下的输出改变量。Shapley value 算法则综合考虑了其它像素的所有可能遮挡情况,并将重要性建模为不同遮挡情况下像素 i 对应输出改变量的平均值。研究已证明,Shapley value 是唯一满足 linearity, dummy, symmetry, efficiency 公理的归因算法。
统一 14 种经验性归因算法的内在机理
在深入研究多种经验性归因算法后,我们不禁思考一个问题:在数学层面上,神经网络的归因究竟在解决什么问题?在众多经验性归因算法的背后,是否蕴含着某种统一的数学建模与范式?为此,我们尝试从归因的定义出发,着眼考虑上述问题。归因,是指每一个输入单元对神经网络输出的重要性分数 / 贡献。那么,解决上述问题的关键在于,(1)在数学层面上建模「输入单元对网络输出的影响机制」,(2)解释众多经验性归因算法是如何利用该影响机制,来设计重要性归因公式。
针对第一个关键点,我们研究发现:每一个输入单元往往通过两种方式影响神经网络的输出。一方面,某一个输入单元无需依赖其他输入单元,可独立作用并影响网络输出,这类影响称为 “独立效应”。另一方面,一个输入单元需要通过与其他输入单元共同协作,形成某种模式,进而对网络输出产生影响,这类影响称为 “交互效应”。我们理论证明了,神经网络的输出可以严谨解构为不同输入变量的独立效应,以及不同集合内输入变量间的交互效应。
其中, 表示第 i 个输入单元的独立效应,
表示第 i 个输入单元的独立效应, 表示集合 S 内多个输入单元间的交互效应。针对第二个关键点,我们探究发现,所有 14 种现有经验性归因算法的内在机理,都可以表示对上述独立效用和交互效用的一种分配,而不同归因算法按不同的比例来分配神经网络输入单元的独立效用和交互效用。具体地,令
表示集合 S 内多个输入单元间的交互效应。针对第二个关键点,我们探究发现,所有 14 种现有经验性归因算法的内在机理,都可以表示对上述独立效用和交互效用的一种分配,而不同归因算法按不同的比例来分配神经网络输入单元的独立效用和交互效用。具体地,令 表示第 i 个输入单元的归因分数。我们严格证明了,所有 14 种经验性归因算法得到的
表示第 i 个输入单元的归因分数。我们严格证明了,所有 14 种经验性归因算法得到的 ,都可以统一表示为下列数学范式(即独立效用和交互效用的加权和):
,都可以统一表示为下列数学范式(即独立效用和交互效用的加权和):
其中, 反映了将第 j 个输入单元的独立效应分配给第 i 个输入单元的比例,
反映了将第 j 个输入单元的独立效应分配给第 i 个输入单元的比例, 表示将集合 S 内多个输入单元间的交互效应分配给第 i 个输入单元的比例。众多归因算法的 “根本区别” 在于,不同归因算法对应着不同的分配比例
表示将集合 S 内多个输入单元间的交互效应分配给第 i 个输入单元的比例。众多归因算法的 “根本区别” 在于,不同归因算法对应着不同的分配比例  。
。
表 1 展示了十四种不同的归因算法分别是如何对独立效应与交互效应进行分配。

图表 1. 十四种归因算法均可以写成独立效应与交互效应加权和的数学范式。其中 分别表示泰勒独立效应和泰勒交互效应,满足
分别表示泰勒独立效应和泰勒交互效应,满足
 ,是对独立效应
,是对独立效应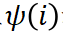 和
和 交互效的细化。
交互效的细化。















评价归因算法可靠性的三大准则
在归因解释研究中,由于无从获得 / 标注神经网络归因解释的真实值,人们无法从实证角度评价某一个归因解释算法的可靠性。“缺乏对归因解释算法可靠性的客观评价标准” 这一根本缺陷,引发了学界对归因解释研究领域的广泛批评与质疑。
而本研究中对归因算法公共机理的揭示,使我们能在同一理论框架下,公平地评价和比较不同归因算法的可靠性。具体地,我们提出了以下三条评估准则,以评价某一个归因算法是否公平合理地分配独立效应和交互效应。
(1)准则一:分配过程中涵盖所有独立效应和交互效应。当我们将神经网络输出解构为独立效应与交互效应后,可靠的归因算法在分配过程中应尽可能涵盖所有的独立效应和交互效应。例如,对 I’m not happy 句子的归因中,应涵盖三个单词 I’m, not, happy 的所有独立效应,同时涵盖 J (I’m, not), J (I’m, happy), J (not, happy), J (I’m, not, happy) 等所有可能的交互效应。
(2)准则二:避免将独立效应和交互分配给无关的输入单元。第 i 个输入单元的独立效应,只应分配给第 i 个输入单元,而不应分配给其它输入单元。类似地,集合 S 内输入单元间的交互效应,只应分配给集合 S 内的输入单元,而不应分配给集合 S 以外的输入单元(未参与交互)。例如,not 和 happy 之间的交互效应,不应分配给单词 I’m。
(3)准则三:完全分配。每个独立效应(交互效应)应当完全分配给对应的输入单元。换句话说,某一个独立效应(交互效应)分配给所有对应输入单元的归因值,加起来应当恰好等于该独立效应(交互效应)的值。例如,交互效应 J (not, happy) 会分配一部分效应 (not, happy) 给单词 not,同时分配一部分效应
(not, happy) 给单词 not,同时分配一部分效应  (not, happy) 给单词 happy。那么,分配比例应满足
(not, happy) 给单词 happy。那么,分配比例应满足 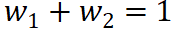 。
。
接着,我们采用这三条评估准则,评估了上述 14 种不同归因算法(如表 2 所示)。我们发现,Integrated Gradients, Expected Gradients, Shapley value, Deep Shap, DeepLIFT Rescale, DeepLIFT RevealCancel 这些算法满足所有的可靠性准则。

表 2. 总结 14 种不同归因算法是否满足三条可靠性评估准则。
作者介绍
本文作者邓辉琦,是中山大学应用数学专业的博士,博士期间曾在香港浸会大学和德州农工大学计算机系访问学习,现于张拳石老师团队进行博士后研究。研究方向主要为可信 / 可解释机器学习,包括解释深度神经网络的归因重要性、解释神经网络的表达能力等。
邓辉琦前期做了很多工作。张老师只是在初期工作结束以后,帮她重新梳理了一遍理论,让证明方式和体系更顺畅一些。邓辉琦毕业前论文不是很多,21 年末来张老师这边以后,在博弈交互的体系下,一年多做了三个工作,包括(1)发现并理论解释了神经网络普遍存在的表征瓶颈,即证明神经网络更不善于建模中等复杂度的交互表征。这一工作有幸被选为 ICLR 2022 oral 论文,审稿得分排名前五(得分 8 8 8 10)。(2)理论证明了贝叶斯网络的概念表征趋势,为解释贝叶斯网络的分类性能、泛化能力和对抗鲁棒性提供了新的视角。(3)从理论层面上解释了神经网络在训练过程中对不同复杂度交互概念的学习能力。
以上是理解并统一14种归因算法,让神经网络具有可解释性的详细内容。更多信息请关注PHP中文网其他相关文章!
 拥抱面部是否7B型号奥林匹克赛车击败克劳德3.7?Apr 23, 2025 am 11:49 AM
拥抱面部是否7B型号奥林匹克赛车击败克劳德3.7?Apr 23, 2025 am 11:49 AM拥抱Face的OlympicCoder-7B:强大的开源代码推理模型 开发以代码为中心的语言模型的竞赛正在加剧,拥抱面孔与强大的竞争者一起参加了比赛:OlympicCoder-7B,一种产品
 4个新的双子座功能您可以错过Apr 23, 2025 am 11:48 AM
4个新的双子座功能您可以错过Apr 23, 2025 am 11:48 AM你们当中有多少人希望AI可以做更多的事情,而不仅仅是回答问题?我知道我有,最近,我对它的变化感到惊讶。 AI聊天机器人不仅要聊天,还关心创建,研究
 Camunda为经纪人AI编排编写了新的分数Apr 23, 2025 am 11:46 AM
Camunda为经纪人AI编排编写了新的分数Apr 23, 2025 am 11:46 AM随着智能AI开始融入企业软件平台和应用程序的各个层面(我们必须强调的是,既有强大的核心工具,也有一些不太可靠的模拟工具),我们需要一套新的基础设施能力来管理这些智能体。 总部位于德国柏林的流程编排公司Camunda认为,它可以帮助智能AI发挥其应有的作用,并与新的数字工作场所中的准确业务目标和规则保持一致。该公司目前提供智能编排功能,旨在帮助组织建模、部署和管理AI智能体。 从实际的软件工程角度来看,这意味着什么? 确定性与非确定性流程的融合 该公司表示,关键在于允许用户(通常是数据科学家、软件
 策划的企业AI体验是否有价值?Apr 23, 2025 am 11:45 AM
策划的企业AI体验是否有价值?Apr 23, 2025 am 11:45 AM参加Google Cloud Next '25,我渴望看到Google如何区分其AI产品。 有关代理空间(此处讨论)和客户体验套件(此处讨论)的最新公告很有希望,强调了商业价值
 如何为抹布找到最佳的多语言嵌入模型?Apr 23, 2025 am 11:44 AM
如何为抹布找到最佳的多语言嵌入模型?Apr 23, 2025 am 11:44 AM为您的检索增强发电(RAG)系统选择最佳的多语言嵌入模型 在当今的相互联系的世界中,建立有效的多语言AI系统至关重要。 强大的多语言嵌入模型对于RE至关重要
 麝香:奥斯汀的机器人需要每10,000英里进行干预Apr 23, 2025 am 11:42 AM
麝香:奥斯汀的机器人需要每10,000英里进行干预Apr 23, 2025 am 11:42 AM特斯拉的Austin Robotaxi发射:仔细观察Musk的主张 埃隆·马斯克(Elon Musk)最近宣布,特斯拉即将在德克萨斯州奥斯汀推出的Robotaxi发射,最初出于安全原因部署了一支小型10-20辆汽车,并有快速扩张的计划。 h
 AI震惊的枢轴:从工作工具到数字治疗师和生活教练Apr 23, 2025 am 11:41 AM
AI震惊的枢轴:从工作工具到数字治疗师和生活教练Apr 23, 2025 am 11:41 AM人工智能的应用方式可能出乎意料。最初,我们很多人可能认为它主要用于代劳创意和技术任务,例如编写代码和创作内容。 然而,哈佛商业评论最近报道的一项调查表明情况并非如此。大多数用户寻求人工智能的并非是代劳工作,而是支持、组织,甚至是友谊! 报告称,人工智能应用案例的首位是治疗和陪伴。这表明其全天候可用性以及提供匿名、诚实建议和反馈的能力非常有价值。 另一方面,营销任务(例如撰写博客、创建社交媒体帖子或广告文案)在流行用途列表中的排名要低得多。 这是为什么呢?让我们看看研究结果及其对我们人类如何继续将


热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

DVWA
Damn Vulnerable Web App (DVWA) 是一个PHP/MySQL的Web应用程序,非常容易受到攻击。它的主要目标是成为安全专业人员在合法环境中测试自己的技能和工具的辅助工具,帮助Web开发人员更好地理解保护Web应用程序的过程,并帮助教师/学生在课堂环境中教授/学习Web应用程序安全。DVWA的目标是通过简单直接的界面练习一些最常见的Web漏洞,难度各不相同。请注意,该软件中

螳螂BT
Mantis是一个易于部署的基于Web的缺陷跟踪工具,用于帮助产品缺陷跟踪。它需要PHP、MySQL和一个Web服务器。请查看我们的演示和托管服务。

SublimeText3汉化版
中文版,非常好用

mPDF
mPDF是一个PHP库,可以从UTF-8编码的HTML生成PDF文件。原作者Ian Back编写mPDF以从他的网站上“即时”输出PDF文件,并处理不同的语言。与原始脚本如HTML2FPDF相比,它的速度较慢,并且在使用Unicode字体时生成的文件较大,但支持CSS样式等,并进行了大量增强。支持几乎所有语言,包括RTL(阿拉伯语和希伯来语)和CJK(中日韩)。支持嵌套的块级元素(如P、DIV),







