最新的斯坦福研究提醒我们不要过于崇信大型模型涌现的能力，因为这只是度量选择结果。

「别太迷信大模型的涌现，世界上哪儿有那么多奇迹？」斯坦福大学的研究者发现，大模型的涌现与任务的评价指标强相关，并非模型行为在特定任务和规模下的基本变化，换一些更连续、平滑的指标后，涌现现象就不那么明显了，更接近线性。

近期，由于研究者们观察到大型语言模型（LLMs），如 GPT、PaLM、LaMDA 可以在不同的任务中表现出所谓的「涌现能力」，这一术语在机器学习领域得到了极大关注：

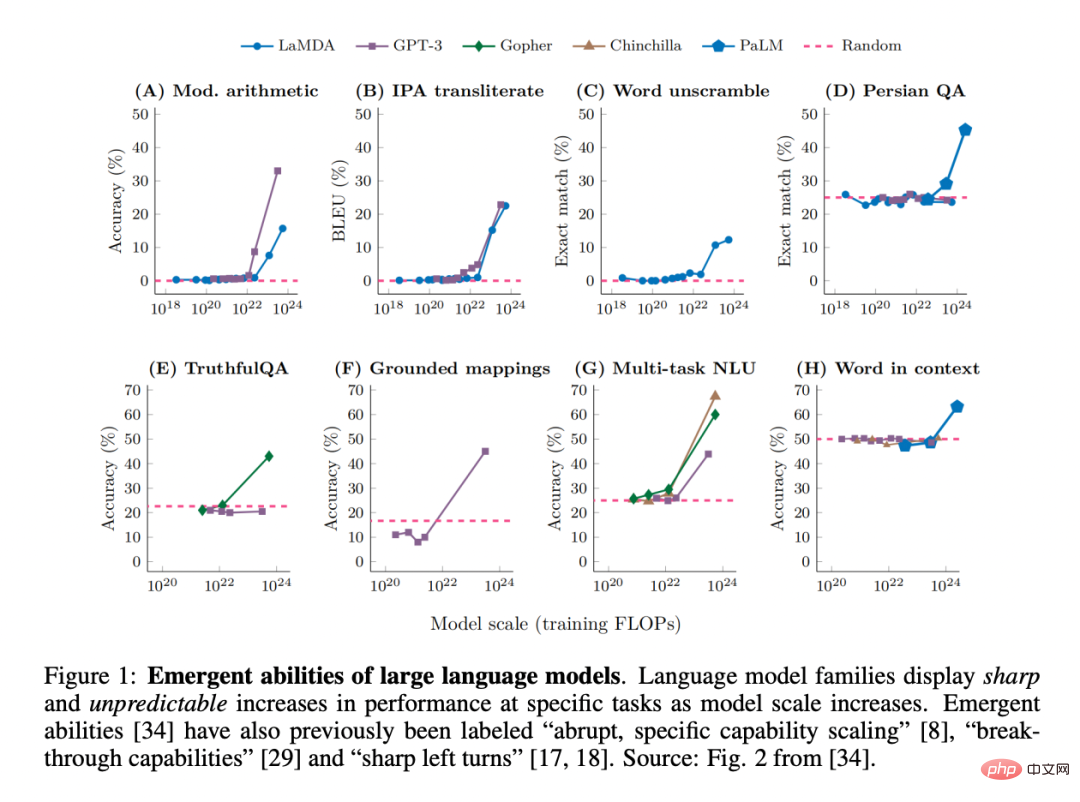
事实上，复杂系统的新兴特性一直以来都是物理学、生物学、数学等学科在研究的重点。

值得注意的一个观点是，诺贝尔物理学奖获得者 P.W.Anderson 提出了「More Is Different」。这一观点认为，随着系统复杂性的增加，新的属性可能会具象化，即使从对系统微观细节的精确定量理解中并不能（容易或根本无法）预测到。

大模型领域的「涌现」如何定义？一种通俗的说法是「在小规模模型中不存在，但在大规模模型中存在的能力」，因此，它们不能通过简单地推断小规模模型的性能改进来预测。

这种涌现的能力可能首先在 GPT-3 家族中被发现。后续的一些工作强调了这一发现：「虽然模型性能在一般水平上是可以预测的，但在特定任务上，其性能有时会在规模上出现相当难以预测的涌现」。事实上，这些涌现能力非常令人惊讶，以至于「突然的、特定的能力扩展」已经被认为是 LLM 的两个最高定义特征之一。此外，「breakthrough capabilities」和「sharp left turns」等术语也被使用。

综上所述，我们可以确定 LLM 涌现能力的两个决定性属性：

1. 敏锐性，从「不存在」到「存在」似乎只是瞬间的过渡；

2. 不可预测性，在看似不可预见的模型规模内过渡。

与此同时，还有一些问题悬而未决：是什么控制了哪些能力会涌现？什么控制着能力的涌现？我们怎样才能使理想的能力更快地涌现，并确保不理想的能力永不涌现？

这些问题与人工智能的安全和对齐息息相关，因为涌现的能力预示着更大的模型可能有一天会在没有警告的情况下获得对危险能力的掌握，这是人类不希望发生的。

在最新的一篇论文中，斯坦福大学的研究者对 LLM 拥有涌现能力的说法提出了质疑。

论文：https://arxiv.org/pdf/2304.15004.pdf

具体而言，此处的质疑针对的是在特定任务中模型输出作为模型规模的函数而发生的涌现和不可预测的变化。

他们的怀疑基于以下观察：似乎只有在非线性或不连续地扩展任何模型的 per-token 错误率的度量下，模型才会出现涌现能力。例如，在 BIG-Bench 任务中，>92% 的涌现能力是这两个度量下出现的：

这就为 LLMs 的涌现能力的起源提出了另一种解释的可能性：尽管模型族的 per-token 错误率会随着模型规模的增加进行平滑、持续且可预测地变化，但看似尖锐和不可预测的变化可能是由研究者选择的测量方法引起的。

也就是说，涌现能力可能是一种海市蜃楼，主要是由于研究者选择了一种非线性或不连续地改变 per-token 错误率的度量，部分原因是由于拥有太少的测试数据，不足以准确估计较小模型的性能（从而导致较小的模型看起来完全不能执行任务），另一部分原因是由于评估了太少的大规模模型。

为了阐述这种解释方式，研究者将其作为一个简单的数学模型，并证明它是如何从数量上再现为支持 LLM 的涌现能力而提供的证据。然后，研究者以三种互补的方式检验了这种解释：

1. 使用 InstructGPT [24]/GPT-3 [3] 模型系列，根据替代假说做出、测试并确认三个预测。

2. 对先前的一些结果进行了元分析，并表明在任务指标 - 模型家族三联体的空间中，出现的能力只出现在某些指标上，而不是任务上的模型家族（列）。该研究进一步表明，在固定的模型输出上，改变度量会导致涌现现象的消失。

3. 故意在不同架构的深度神经网络中诱导出多个视觉任务的涌现能力（这在以前从未被证明过），以显示类似的度量选择如何诱导出看似涌现的能力。

检验一：InstructGPT/GPT-3 模型系列分析

研究者选择了 GPT 系列模型进行进一步分析，原因在于它是可公开查询的，这一点和其他模型系列不同（例如 PaLM、LaMDA、Gopher、Chinchilla）。在此前的研究中，GPT 系列模型被认为在整数算术任务中展示出涌现能力。此处，研究者也选择了整数算术这一任务。

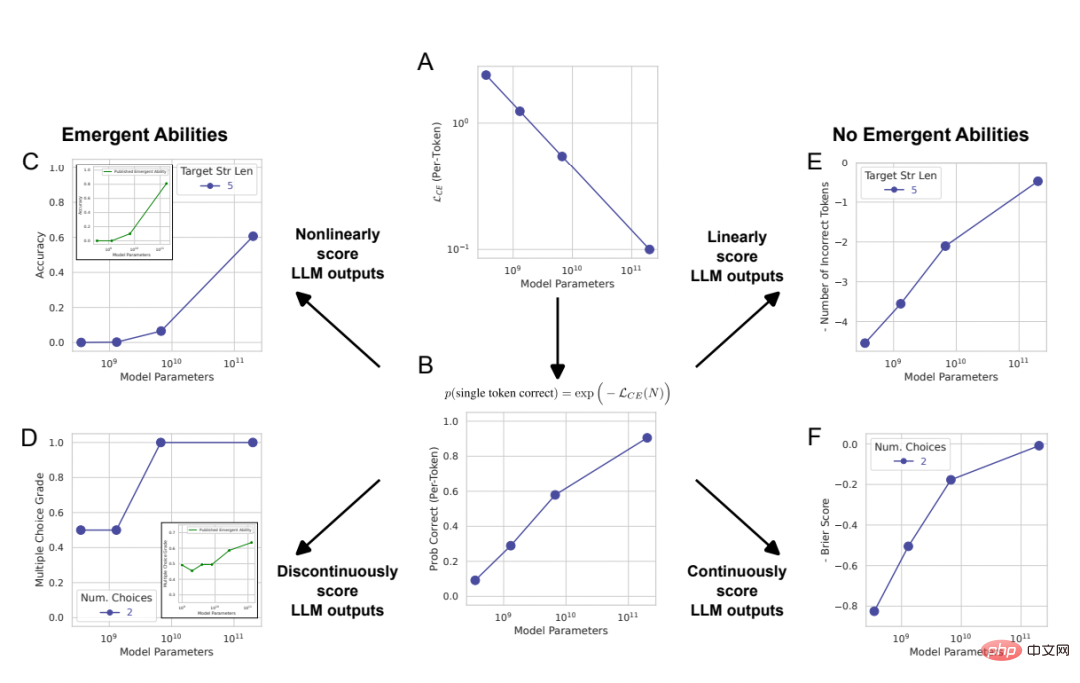
图 2: 大型语言模型的涌现能力是研究者分析的创造物，而不是模型输出随规模变化的根本性变化。

正如第 2 节中用数学和图表解释的那样，研究者提出的替代解释可以预测出三个结果：

1. 随着模型规模提升，如果将度量从非线性 / 不连续的度量（图 2CD）换成线性 / 连续的度量（图 2EF），那么应该会有平滑的、连续的、可预测的性能提升。

2. 对于非线性的度量，如果通过增大测试数据集的大小而提升所测模型性能的分辨率，那么应该能让模型得到平滑的、连续的、可预测的提升，并且该提升的比例与所选度量的可预测的非线性效应是相对应的。

3. 无论使用什么度量指标，提升目标字符串长度都应该会对模型性能产生影响，该影响是长度为 1 的目标性能的一个函数：对于准确度是近乎几何的函数，对于 token 编辑距离是近乎准线性的函数。

为了测试这三个预测结论，研究者收集了 InstructGPT/GPT-3 系列模型在两个算术任务上的字符串输出结果：使用 OpenAI API 执行 2 个两位数整数之间的两样本乘法以及 2 个四位数整数之间的两样本加法。

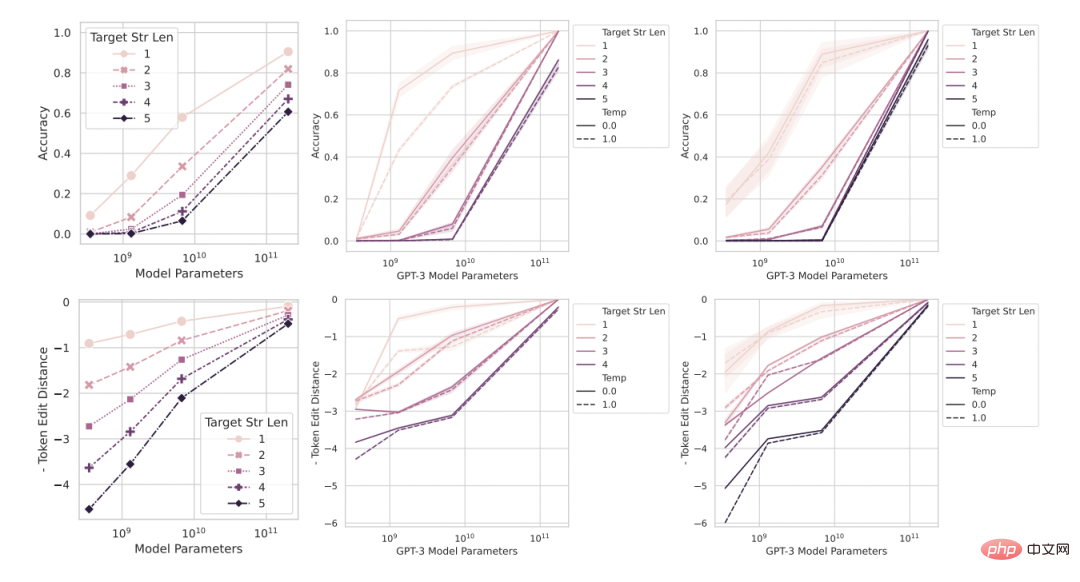
图 3：随着模型规模提升，改变度量可以为性能带来平滑、连续、可预测的改变。

从左至右：数学模型，2 个两位数整数乘法任务， 2 个四位数整数加法任务。上方的图是使用一个非线性度量（如准确度）而测得的模型性能，可看到 InstructGPT/GPT-3 系列模型的性能在目标长度更长时显得锐利和不可预测。而下方的图是使用一个线性度量（如 token 编辑距离）而测得的模型性能，此系列模型表现出了平滑的、可预测的性能提升，这是研究者宣称的涌现产生的能力。

预测：涌现能力在线性度量下会消失

在这两个整数乘法和加法任务上，如果目标字符串的长度是 4 或 5 位数字并且性能的度量方式是准确度（图 3 上一行图），那么 GPT 系列模型会展现出涌现的算术能力。但是，如果将一个度量从非线性换成线性，同时保持模型的输出固定，那么该系列模型的性能会得到平滑、连续和可预测的提升。这就确认了研究者的预测，由此表明锐利和不确定性的来源是研究者所选择的度量，而非模型的输出的变化。还可以看到，在使用 token 编辑距离时，如果将目标字符串的长度从 1 增大至 5，那么可预见该系列模型的性能会下降，并且下降趋势是近乎准线性的，这符合第三个预测的前半部分。

预测：涌现能力随着更高的分辨率评估的出现而消失

接下来是第二个预测：即使是用准确度等非线性度量，更小模型的准确度也不会为零，而是高于偶然性的非零值，其比例是与选择使用准确度为度量相对应的。为了提升分辨率，以进一步能准确估计模型准确度，研究者还生成了其它一些测试数据，然后他们发现：不管是在整数乘法任务上还是在整数加法任务上，InstructGPT/GPT-3 系列的所有模型都得到了超过偶然性的正值准确度（图 4）。这验证了第二个预测。可以看到，随着目标字符串长度增大，准确度会随目标字符串的长度而呈现近乎几何式的下降，这符合第三个预测的后半部分。这些结果还表明研究者选择的准确度会产生一些我们应该能预料到的（近似）效果，即随目标长度而近乎几何式地衰减。

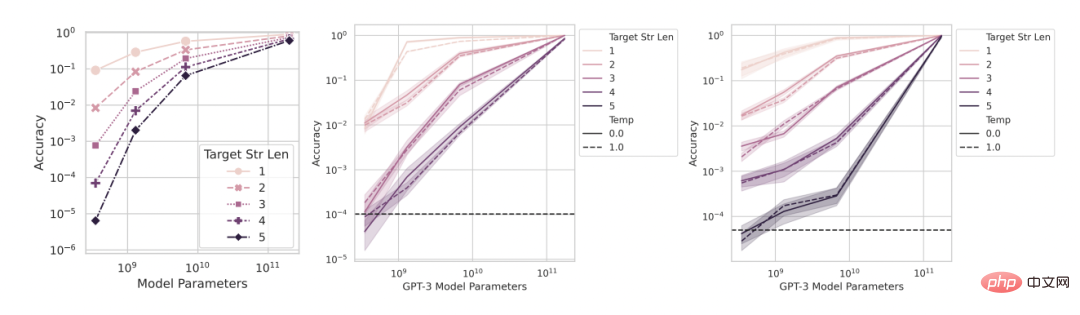
图 4：使用更多测试数据集得到了更好的准确度估计，这揭示出性能的变化是平滑的、连续的和可预测的。

从左至右：数学模型，2 个两位数整数乘法任务， 2 个四位数整数加法任务。通过生成更多测试数据来提升分辨率，揭示出即使是在准确度度量上，InstructGPT/GPT-3 系列模型的性能也是超出偶然结果的，并且其在两种涌现能力上的提升是平滑的、连续的和可预测的，这两种涌现能力的结果在定性上是与数学模型相符的。

检验二：模型涌现的元分析

由于 GPT 系列模型是可以公开查询使用的，因此可以对它们进行分析。但是，其它一些也有人声称具备涌现能力的模型（比如 PaLM、Chinchilla、Gopher）却并不是公开可用的，它们生成的输出也没有公开，这意味着研究者在分析已发表结果时是受限的。研究者基于自己提出的替代假设给出了两个预测：

• 第一，在「任务 - 度量 - 模型系列」三元组的「群体层面（population level）」上，当选择使用非线性和 / 或非连续度量来评估模型性能时，模型应当会在任务上表现出涌现能力。
• 第二，对于展现出了涌现能力的特定「任务 - 度量 - 模型系列」三元组，如果将度量改变成线性和 / 或连续度量，那么涌现能力应该会被消除。

为了测试这两个假设，研究者调查了声称在 BIG-Bench 评估套件上涌现出的能力，因为在该套件上的基准是公开可用的，并且也有很好的文档。

预测：涌现能力应该主要出现在非线性 / 非连续度量上

为了测试第一个预测，研究者分析了在哪些指标上，不同的「任务 - 模型系列」配对是否会出现涌现能力。为了确定一个「任务 - 度量 - 模型系列」三元组是否可能展现出涌现能力，他们借用了论文《Beyond the imitation game: Quantifying and extrapolating the capabilities of language models》中引入的定义。令 y_i ∈ R 表示模型大小为 x_i ∈ R 时的模型性能，并使得 x_i < x_i+1，则涌现分数为：

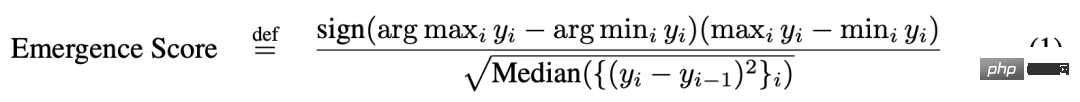
结果研究者发现，BIG-Bench 使用的大多数度量中没有表现出涌现能力的「任务 - 模型系列」配对：在人们偏好的 39 个 BIG-Bench 度量中，至多 5 个展现出了涌现能力（图 5A）。这 5 个大都是非线性的 / 非连续的，如精确字符串匹配、多选择分级、ROUGE-L-Sum。值得注意的是，由于 BIG-Bench 通常使用多项度量来评估模型的任务表现，因此在其它度量下缺乏涌现能力这一现象说明：当使用其它度量来评价模型输出时，涌现能力并不会出现。

由于涌现分数仅表明有涌现能力，因此研究者还进一步分析了论文《137 emergent abilities of large language models》中人工标注的「任务 - 度量 - 模型系列」三元组。人工标注的数据表明 39 个度量中仅有 4 个表现出了涌现能力（图 5B），并且它们中的 2 个就占到了所宣称的涌现能力的 92% 以上（图 5C）。多选择分级和精确字符串匹配。多选择分级是非连续的，精确字符串匹配是非线性的（在目标长度度量上的变化是近乎几何式的）。总体而言，这些结果说明涌现能力仅出现在非常少量的非线性和 / 或非连续度量上。

图 5：仅有少数度量会出现涌现能力。(A) 在人们偏好的 39 个 BIG-Bench 度量中，至多只有 5 个度量上可能出现了涌现能力。(B) 所引论文中人工标注的数据表明仅有 4 个人们偏好的度量表现出了涌现能力。(C) 涌现能力中 > 92% 都出现在以下两个度量之一上：多选择分级和精确字符串匹配。

预测：如果替代非线性 / 非连续度量，涌现能力应该会被消除

对于第二个预测，研究者分析了前文所引论文中人工标注的涌现能力。他们关注的是 LaMDA 系列，因为其输出可通过 BIG-Bench 获取，而其它模型系列的输出无法这样获取。在已经发表的 LaMDA 模型中，最小的有 20 亿个参数，但 BIG-Bench 中的许多 LaMDA 模型都小很多，而且研究者表示由于无法确定这些更小模型的来源，因此没有在分析中考虑它们。在分析中，研究者认定了在多选择分级度量上 LaMDA 在哪些任务上展现出了涌现能力，然后他们提出了问题：当使用另一个 BIG-Bench 度量 Brier 分数时，LaMDA 能否在同样的任务上展现出涌现能力。Brier 分数是一套严格适当（strictly proper）的评分规则，其度量的是互斥结果的预测；对于一个二元结果的预测，Brier 分数简化成了结果及其预测概率质量之间的均方误差。

研究者发现，当非连续度量多选择分级变成连续度量 Brier 分数时（图 6），LaMDA 的涌现能力消失了。这进一步说明涌现能力的成因并非是随规模增长而导致的模型行为的本质变化，而是对非连续度量的使用。

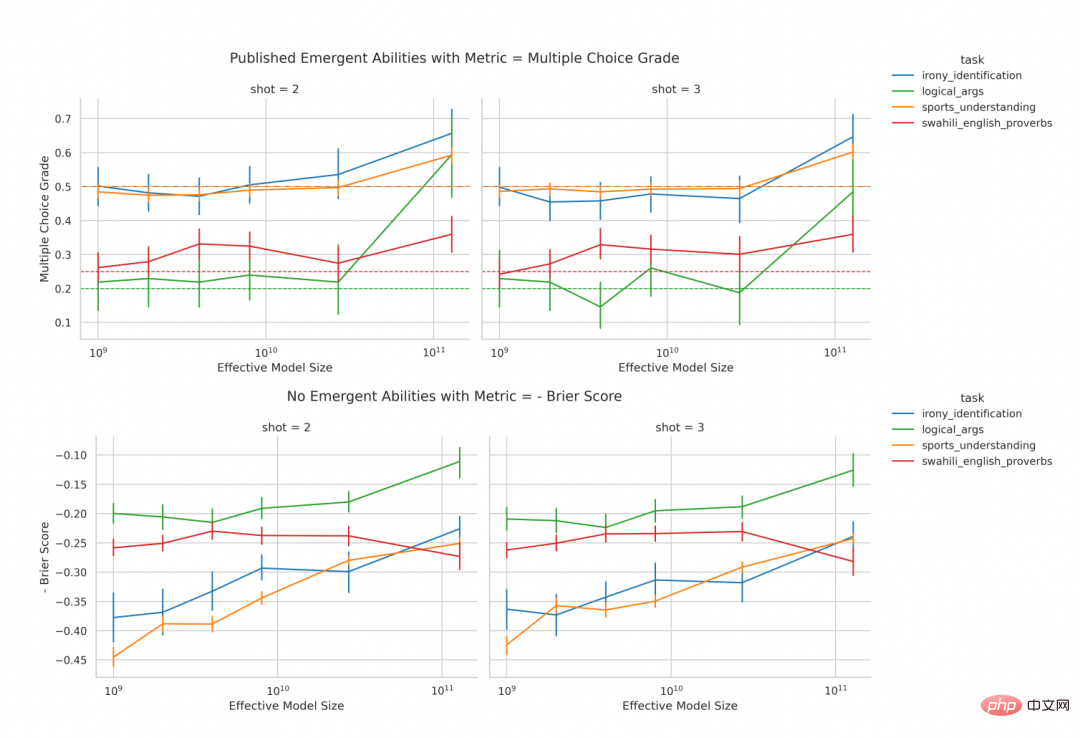
图 6：在任务和模型系列保持不变的前提下改变 BIG-Bench 度量会导致涌现能力消失。上一行：当使用的是一个非连续度量（多选择分级）时，LaMDA 模型系列展现出了涌现能力。下一行：当使用的是一个连续的 BIG-Bench 度量（Brier 分数）时，LaMDA 模型系列在同样任务上不再有涌现能力。

检验三：诱导 DNN 出现涌现能力

研究者的观点是可以通过度量的选择来诱导模型产生涌现能力；为了证明这一点，他们展示了如何让不同架构（全连接、卷积、自注意力）的深度神经网络产生涌现能力。这里研究者重点关注的是视觉任务，原因有二。第一，人们现在主要关注大型语言模型的涌现能力，因为对于视觉模型而言，目前还没有观察到模型能力从无突然转变到有的现象。第二，某些视觉任务用大小适中的网络就足以解决，因此研究者可以完整构建出跨多个数量级规模的模型系列。

卷积网络涌现出对 MNIST 手写数字的分类能力

研究者首先诱导实现 LeNet 卷积神经网络系列涌现出分类能力，训练数据集是 MNIST 手写数字数据集。这个系列展现出了随参数数量增长，测试准确度平滑提升的现象（图 7B）。为了模拟有关涌现的论文中使用的准确度度量，这里使用的是子集准确度（subset accuracy）：如果该网络从 K 个（独立的）测试数据中正确分类出了 K 个数据，那么该网络的子集准确度为 1，否则为 0。基于这一准确度定义，在 K 从 1 增长到 5 的设定中，该模型系列展现出了「涌现」能力，从而能够正确分类 MNIST 数字集，尤其是结合了模型大小的稀疏采样时（图 7C）。这个卷积系列的涌现分类能力在定性分析上符合已发表论文中的涌现能力，比如在 BIG-Bench 的地形测绘任务上的结果（图 7A）。

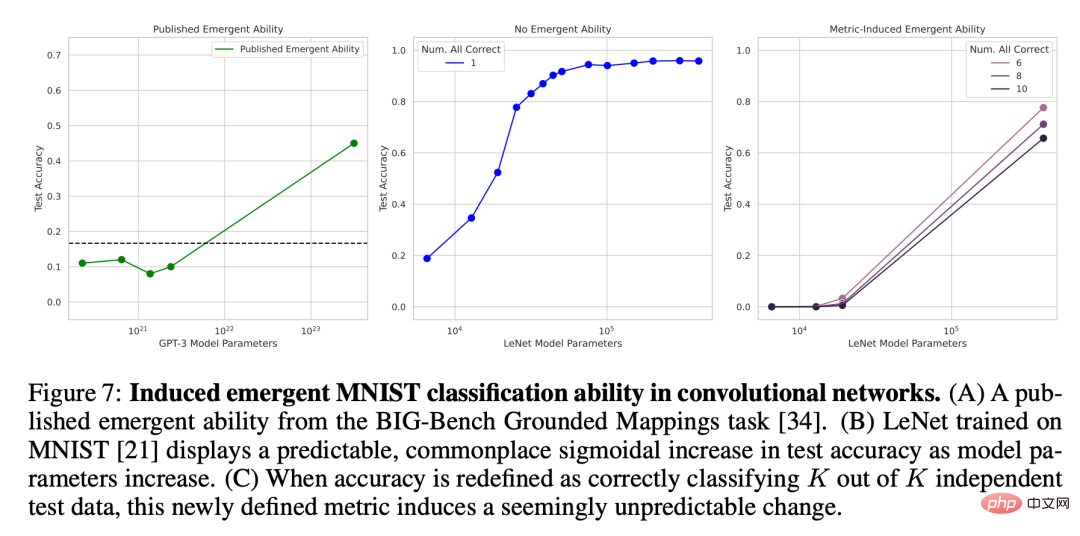
图 7：在卷积网络中诱导出涌现的 MNIST 分类能力。(A) 一篇已发表论文中的基于 BIG-Bench 地形测绘任务的涌现能力。(B) 在 MNIST 上训练的 LeNet 表现出：随模型参数数量增长，测试准确度展现出预测的、普遍的、S 形的增长。(C) 当把准确度重新定义成从 K 个独立测试数据中正确分类出 K 个时，这个新定义的度量会诱导出一种似乎在预料之外的变化。

非线性自动编码器在 CIFAR100 自然图像集上涌现出重建能力

为了凸显出研究者所选度量的锐利度是涌现能力的原因，并且为了表明这种锐利度不仅限于准确度等度量，研究者又诱导在 CIFAR100 自然图像集上训练的浅度（即单隐藏层）非线性自动编码器涌现出重建图像输入的能力。为此，他们刻意定义了一个新的用于衡量模型能力的不连续度量，该度量为平方重建误差低于固定阈值 c 的测试数据的平均数量：

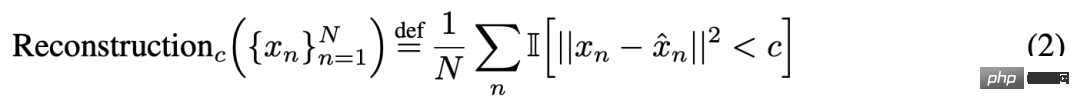
其中 I (・) 是一个随机指示变量，x^n 是自动编码器对 x_n 的重建。研究者检视了自动编码器瓶颈单元的数量，然后发现随模型规模增长，网络的均方重建误差会表现出平滑的下降趋势（图 8B），但如果使用新定义的重建度量，对于选定的 c，这个自动编码器系列在重建该数据集上展现出的能力是锐利的和几乎不可预测的（图 8C），这个结果在定性分析上符合已发表论文中的涌现能力，比如 BIG-Bench 中的 Periodic Elements（周期性元素）任务（图 8A）。

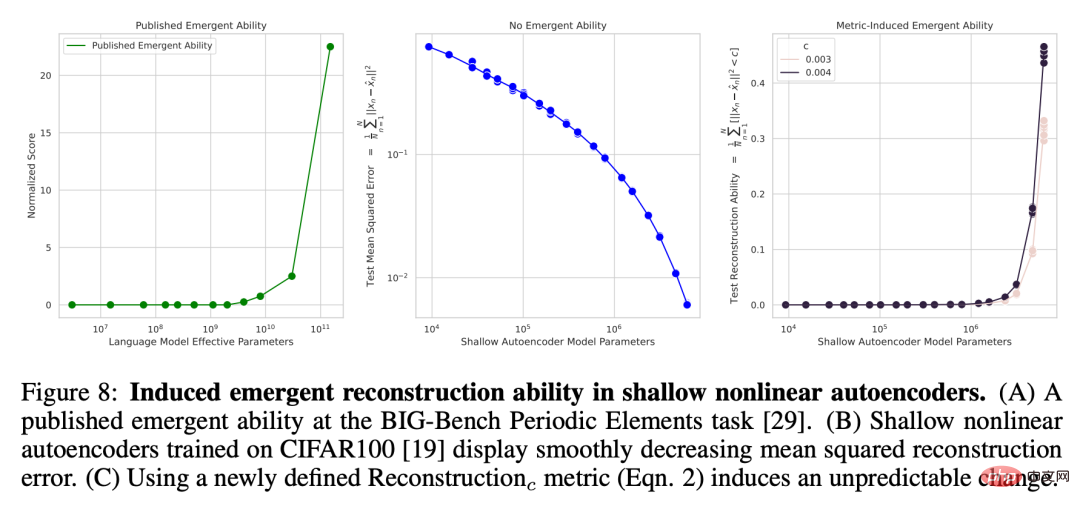
图 8：在浅度非线性自动编码器中诱导出涌现的重建能力。(A) 一篇已发表论文中的基于 BIG-Bench 周期性元素任务的涌现能力。(B) 在 CIFAR100 上训练的浅度非线性自动编码器展现出了平滑下降的均方重建误差。(C) 使用新定义的重建度量（公式 2）诱导出了不可预测的变化。

自回归 Transformer 在 Omniglot 字符集上涌现出了分类能力

接下来是 Transformer 的涌现能力，其使用的是自回归方法来分类 Omniglot 手写字符。研究者使用的实验设置是类似的：Omniglot 图像先由卷积层嵌入，然后以 [嵌入图像，图像类别标签] 配对组成序列的方式输入仅解码器的 Transformer，而该 Transformer 的训练目标是预测 Omniglot 类别标签。研究者是在长度为 L ∈ [1, 5] 的序列上测量图像分类性能，同样是通过子集准确度来度量：如果所有 L 图像都分类正确（图 9B）则子集准确度为 1，否则为 0。Causal Transformer 在正确分类 Omniglot 手写字符任务上似乎展现出了涌现能力（图 9C），该结果在定性分析上符合已发表论文中的涌现能力，比如大规模多任务语言理解（图 9A）。

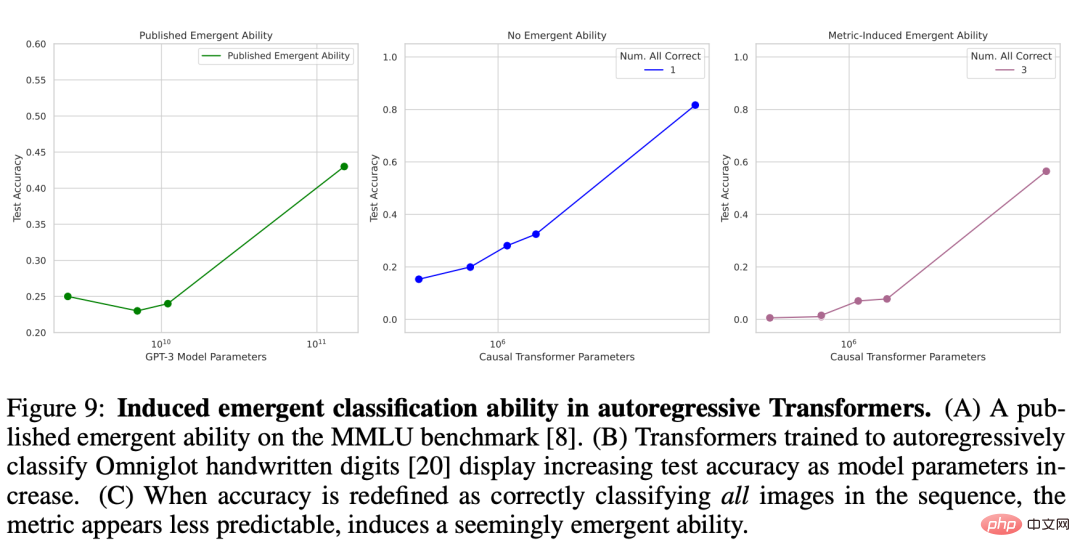
图 9：在自回归 Transformer 中诱导出涌现的分类能力。(A) 一篇已发表论文中基于 MMLU 基准的涌现能力。(B) 随模型参数增多，使用自回归方法来分类 Omniglot 手写数字的 Transformer 的测试准确度也表现为增长。(C) 当将准确度重新定义为正确分类序列中的所有图像时，该指标更难被预测，这似乎说明诱导出了涌现能力。

以上是最新的斯坦福研究提醒我们不要过于崇信大型模型涌现的能力，因为这只是度量选择结果。的详细内容。更多信息请关注PHP中文网其他相关文章！