战胜困难：赌场利润背后的数学

您有没有想过为什么赌场似乎总是赢钱？在“战胜困难：赌场利润背后的数学”中，我们将探索确保赌场长期盈利的简单数学和巧妙策略。通过易于理解的示例和蒙特卡洛模拟，我们将揭示房子边缘背后的秘密。准备好探索赌场如何扭转局面！

了解庄家优势

赌场优势是赌场世界的基本概念。它代表赌场期望从玩家每次下注中获得的平均利润。本质上，它是赌场长期保留的每笔赌注的百分比。

赌场优势的存在是因为赌场不根据游戏的“真实赔率”支付获胜赌注。真实赔率代表事件发生的实际概率。通过以略低的赔率支付，赌场可以确保他们随着时间的推移赚取利润。

赌场优势 (HE) 定义为赌场利润，以玩家原始赌注的百分比表示。

** 欧式轮盘 ** 只有一个绿色零，总共有 37 个数字。如果玩家在红色下注 1 美元，他们有 18/37 的机会赢得 1 美元，有 19/37 的机会输掉 1 美元。期望值为：

期望值=( 1 × 18/37 ​)+( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2.7%

因此，在欧式轮盘赌中，赌场优势 (HE) 约为 2.7%。

让我们自己制作一个游戏来更好地理解它，一个简单的掷骰子游戏。

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll <= 50:
        print(roll, 'You rolled between 1 and 50 and lost.')
        return False
    else:
        print(roll, 'You rolled between 51 and 99 and won! Keep playing!')
        return True

在这个游戏中：

• 如果掷骰值为 100，则玩家有 1/100 的几率失败。

• 如果掷骰结果在 1 到 50 之间，玩家有 50/100 的几率失败。

• 如果掷骰结果在 51 到 99 之间，玩家有 49/100 的获胜机会。

期望值 =(1× 49/100​) + ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100​ ≈ −2%

因此，赌场优势为2%。

了解蒙特卡罗模拟

蒙特卡罗模拟是一种强大的工具，用于通过对过程进行大量模拟并观察结果来理解和预测复杂系统。在赌场的背景下，蒙特卡洛模拟可以对各种投注场景进行建模，以显示赌场优势如何确保长期盈利能力。让我们探索蒙特卡洛模拟的工作原理以及如何将它们应用于简单的赌场游戏。

什么是蒙特卡罗模拟？

蒙特卡洛模拟涉及生成随机变量来多次模拟过程并分析结果。通过执行数千甚至数百万次迭代，我们可以获得可能结果的分布，并深入了解不同事件发生的可能性。

将蒙特卡罗模拟应用于掷骰子游戏

我们将使用蒙特卡罗模拟来模拟我们之前讨论的掷骰子游戏。这将帮助我们了解赌场优势如何随着时间的推移影响游戏的盈利能力。

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins += 1
        else:
            losses += 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

解释结果

在这个模拟中，我们运行骰子游戏 10,000,000 次来观察输赢百分比。鉴于之前计算的赌场优势 (2%)，我们预计输钱百分比将略高于赢钱百分比。

运行模拟后，您可能会看到如下结果：

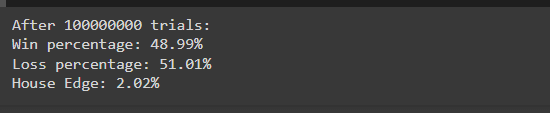
这些结果与理论概率密切相关（49% 获胜，51% 失败），展示了赌场优势在大量试验中的表现。轻微的不平衡保证了赌场的长期盈利能力。

可视化短期胜利和长期损失

蒙特卡洛模拟对于通过重复随机抽样来建模和预测结果非常有用。在赌博的背景下，我们可以使用蒙特卡罗模拟来了解不同投注策略的潜在结果。

我们将模拟一个投注者在每一轮中都下了相同的初始赌注，并观察他们的账户价值在指定的赌注数量上如何变化。

以下是我们如何使用 Matplotlib 模拟和可视化投注过程：

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager <= wager_count:
        if roll_dice():
            value += wager
        else:
            value -= wager

        wX.append(current_wager)
        vY.append(value)
        current_wager += 1

    return wX, vY

# Parameters for simulation
funds = 10000
initial_wager = 100
wager_count = 1000

# Run the simulation for a single bettor
wager_counts, account_values = bettor_simulation(funds, initial_wager, wager_count)

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wager_counts, account_values, label='Bettor 1', color='blue')
plt.xlabel('Wager Count')
plt.ylabel('Account Value')
plt.title('Betting Journey: Short-Term Wins vs Long-Term Losses')
plt.grid(True)
plt.legend()

# Highlighting the short-term and long-term trend
plt.axhline(y=funds, color='gray', linestyle='--', label='Initial Funds')
plt.axhline(y=account_values[0], color='green', linestyle='--', label='Starting Account Value')
plt.axhline(y=account_values[-1], color='red', linestyle='--', label='Final Account Value')

plt.legend()
plt.show()

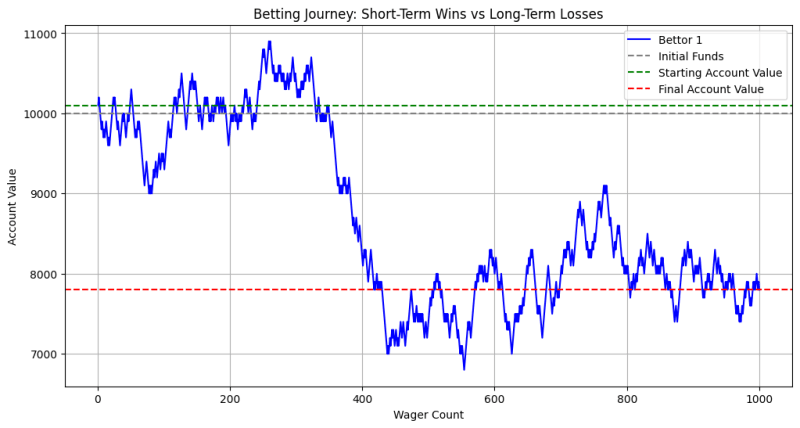
此图说明了投注者的账户价值如何因输赢而随时间波动。最初，可能会有一段获胜的时期（绿线高于起始值），但随着投注次数的增加，赌场优势的累积效应变得明显。最终，投注者的账户价值往往会下降到接近或低于初始资金（灰线），表明长期损失。

结论

了解赌场利润背后的数学原理，可以通过赌场优势的概念揭示赌场在每场游戏中的明显优势。尽管偶尔会获胜，但赌场游戏中内置的概率确保大多数玩家随着时间的推移会输钱。蒙特卡洛模拟生动地说明了这些动态，表明由于赌场的统计优势，即使是短期胜利也可以掩盖长期损失。这种对赌场盈利能力数学确定性的洞察强调了明智决策和负责任赌博实践的重要性。

接下来，我们可以探索其他可视化或变化，例如比较不同的投注策略或分析不同的初始投注对投注者结果的影响。

保持联系：

• GitHub：ezhillragesh

• 推特：ezhillragesh

• 网站：ragesh.me

请随时分享您的想法、提出问题并参与讨论。

编码愉快！

以上是战胜困难：赌场利润背后的数学的详细内容。更多信息请关注PHP中文网其他相关文章！