斯奇拉姆排序 - 基於公平性的排序學習

在 2023 年舉行的國際學術會議 AIBT 2023 上，Ratidar Technologies LLC 發表了一篇基於公平性的排序學習演算法，並榮獲該會議的最佳論文報告獎。該演算法名為斯奇拉姆排序 (Skellam Rank)，充分利用了統計學原理，結合了Pairwise Ranking和矩陣分解技術，以解決推薦系統中的準確率和公平性問題。由於推薦系統中創新的排序學習演算法很少，斯奇拉姆排序演算法表現出色，因此在會議上獲得了研究獎項。以下將介紹斯奇拉姆演算法的基本原理：

我們先回想一下泊松分佈：

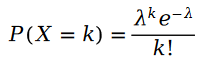
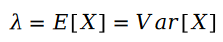
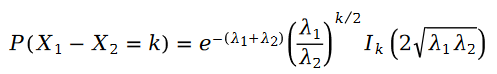
#泊松分佈的參數 的計算公式如下：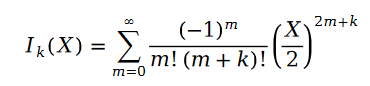

#兩個泊松變數的差異是斯奇拉姆分佈：

在公式中，我們有：

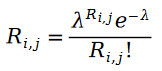
函數 叫做第一類貝塞爾函數。

有了這些最基本的統計學中的概念，以下讓我們來建立一個 Pairwise Ranking 的排序學習推薦系統吧！

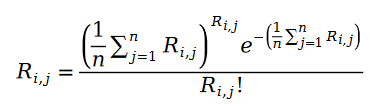
我們先認為使用者給物品的評分是個泊松分佈的概念。也就是說，使用者物品評分值服從以下機率分佈：

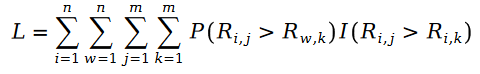
#之所以我們可以把使用者給物品打分數的過程描述為泊松過程，是因為用戶物品評分存在馬太效應，也就是說評分越高的用戶，評分的人越多，以至於我們可以用某個物品的評分的人的數量來近似該物品的評分的分佈。給某個物品打分數的人數服從什麼隨機過程？自然而然的，我們就會想到泊松過程。因為使用者給物品打分數的機率和該物品有多少人打分的機率相近，我們自然也就可以用泊松過程來近似使用者給物品打分的這一過程了。

我們下面把泊松過程的參數用樣本資料的統計量取代，得到下面的公式：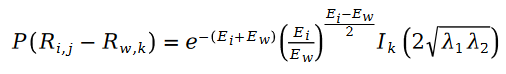

我們下面定義Pariwise Ranking 的最大似然函數公式。眾所周知，所謂Pairwise Ranking 指的是我們利用最大似然函數來求解模型參數，使得模型能夠最大程度地保持資料樣本中已知的排序對的關係：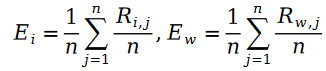

因為公式中的R 是泊松分佈，所以它們的差值，就是斯奇拉姆分佈，也就是說：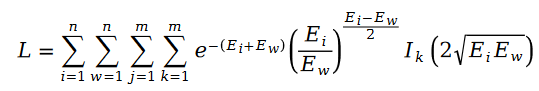

##其中變數E 是如下定義的：######################我們把斯奇拉姆分佈的公式帶入最大似然函數的損失函數L ，得到如下公式：######################在變數E 中出現的使用者評分值R ，我們利用矩陣分解的方式進行求解。將矩陣分解中的參數使用者特徵向量 U 和物品特徵向量 V 作為待求解變數：######

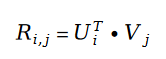
這裡我們先回顧矩陣分解的概念。矩陣分解的概念是在 2010 年左右的時候提出的推薦系統演算法，該演算法可以說是歷史上最成功的推薦系統演算法之一。時至今日，仍有大量的推薦系統公司利用矩陣分解演算法作為線上系統的baseline，而時下大熱的經典推薦演算法DeepFM 中的重要組件Factorization Machine，也是推薦系統演算法中的矩陣分解演算法後續的改進版本，和矩陣分解有千絲萬縷的關係。矩陣分解演算法有一個里程碑論文，是 2007 年的 Probabilistic Matrix Factorization，作者利用統計學習模型對矩陣分解這個線性代數中的概念重新建模，使得矩陣分解第一次有了紮實的數學理論基礎。

矩陣分解的基本概念，是利用向量的點乘，在對使用者評分矩陣進行降維的同時高效的預測未知的使用者評分。矩陣分解的損失函數如下：

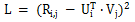
矩陣分解演算法有許多的變種，例如上海交大提出的SVDFeature，把向量U 和V 用線性組合的形式進行建模，使得矩陣分解的問題變成了特徵工程的問題。 SVDFeature 也是矩陣分解領域的里程碑論文。矩陣分解可以被應用在Pairwise Ranking 中用以取代未知的用戶評分，從而達到建模的目的，經典的應用案例包括Bayesian Pairwise Ranking 中的BPR-MF 演算法，而斯奇拉姆排序演算法就是藉鑑了同樣的思路。

我們用隨機梯度下降對斯奇拉姆排序演算法進行求解。因為隨機梯度下降在求解過程中，可以對損失函數進行大量的簡化從而達到求解的目的，我們的損失函數變成了下面的公式：

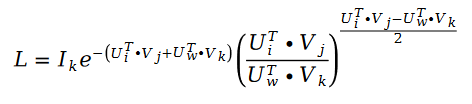
利用隨機梯度下降對未知參數U 和V 進行求解，我們得到了迭代公式如下：

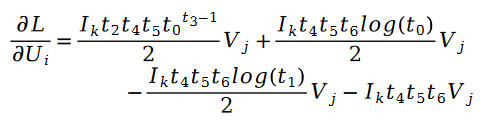
##其中：

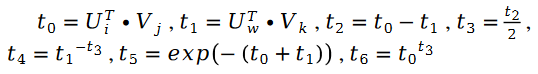
另外有：

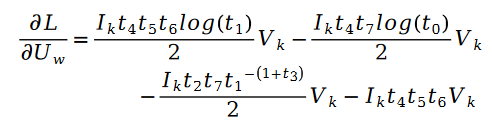
其中：

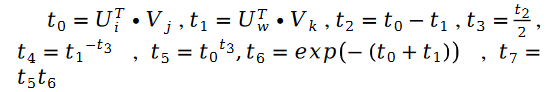
對於未知參數變數V 的求解類似，我們有以下公式：

# #其中：

另外有：

其中：

整個演算法的流程，我們用以下的偽代碼來展示：

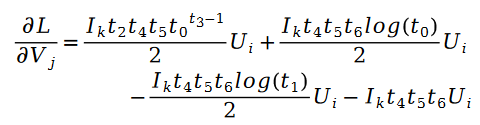
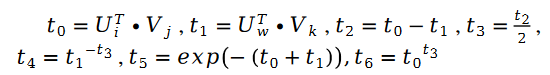
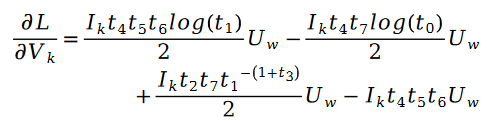
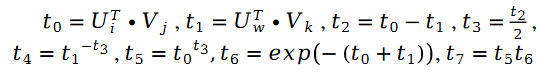
為了驗證演算法的有效性，論文作者在 MovieLens 1 Million Dataset 和 LDOS-CoMoDa Dataset 上進行了測試。第一個數據集包含了 6040 個用戶和 3706 部電影的評分，整個評分數據集大概有 100 萬評分數據，是推薦系統領域最知名的評分數據集合之一。第二個資料集合來自斯洛維尼亞，是網路上不多見的基於場景的推薦系統資料集合。該數據集合包含了 121 個用戶和 1232 部電影的評分。作者將斯奇拉姆排序和另外9 種推薦系統演算法進行了對比，主要評估指標為MAE （Mean Absolute Error，用來測試準確性）和Degree of Matthew Effect （主要用來測試公平性）：

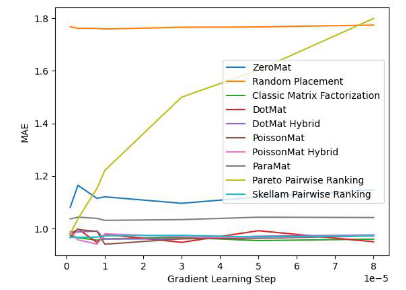
圖1. MovieLens 1 Million Dataset (MAE 指標)

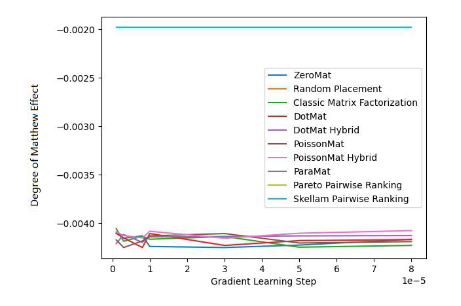
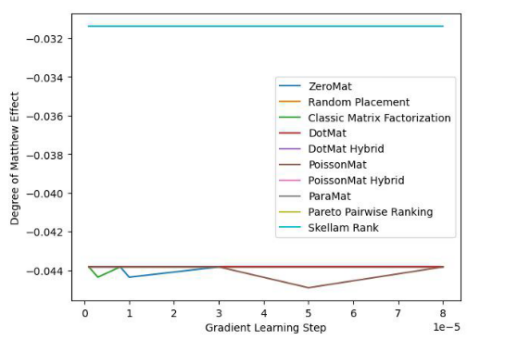
#圖2. MovieLens 1 Million Dataset (Degree of Matthew Effect 指標)

透過圖1 和圖2 ，我們發現斯奇拉姆排序在MAE 這項指標上表現優異，但在Grid Search 的整個實驗過程中，無法一直保證效能優於其他演算法。但在圖 2 中，我們發現斯奇拉姆排序在公平性指標上一騎絕塵，遙遙領先另外 9 種推薦系統演算法。

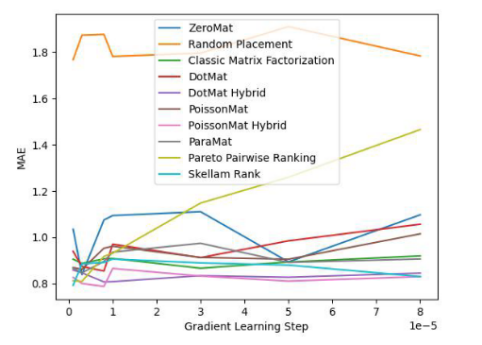
下面我們來看看演算法在LDOS-CoMoDa 資料集合上的表現：

##############圖3. LDOS-CoMoDa Dataset (MAE 指標)#####################圖4.LDOS-CoMoDa Dataset (Degree of Matthew Effect 指標)##### #######透過圖3和圖4，我們了解到斯奇拉姆排序在公平性指標上一騎絕塵，在準確度指標上表現優異。結論和上一個實驗類似。 ############斯奇拉姆排序結合了泊松分佈、矩陣分解和 Pairwise Ranking 等概念，是一個不可多得的推薦系統排序學習演算法。在技​​術領域，掌握排序學習技術的人只佔掌握深度學習的人的人數的1/6，因此排序學習屬於稀缺技術。而能夠在推薦系統領域發明原創性排序學習的人才更是少之又少。排序學習演算法，把人們從評分預測的狹隘視角中解放了出來，讓人們意識到最重要的事情是順序，而不是分數。基於公平性的排序學習，目前在資訊檢索領域中大火，特別是 SIGIR 等頂會，非常歡迎基於公平性的推薦系統的論文，希望能夠得到讀者們的關注。 ############作者簡介############汪昊，前 Funplus 人工智慧實驗室負責人。曾在 ThoughtWorks、豆瓣、百度、新浪等公司擔任技術和技術主管。在網路公司和金融科技、遊戲等公司任職 12 年，對於人工智慧、電腦圖形和區塊鏈等領域有著深刻的見解和豐富的經驗。在國際學術會議和期刊發表論文 42 篇，獲得IEEE SMI 2008 最佳論文獎、ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 最佳論文報告獎。 ############

以上是斯奇拉姆排序 - 基於公平性的排序學習的詳細內容。更多資訊請關注PHP中文網其他相關文章！