借助 Lean,陶哲軒又開始了新的專案。





以上是陶哲軒上新專題:Lean中證明質數定理,研究藍圖都建好了的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 META的新AI助手:生產力助推器還是時間下沉?May 01, 2025 am 11:18 AM
META的新AI助手:生產力助推器還是時間下沉?May 01, 2025 am 11:18 AMMeta攜手Nvidia、IBM和Dell等合作夥伴,拓展了Llama Stack的企業級部署整合。在安全方面,Meta推出了Llama Guard 4、LlamaFirewall和CyberSecEval 4等新工具,並啟動了Llama Defenders計劃,以增強AI安全性。此外,Meta還向10個全球機構(包括致力於改善公共服務、醫療保健和教育的初創企業)發放了總額150萬美元的Llama Impact Grants。 由Llama 4驅動的全新Meta AI應用,被設想為Meta AI
 80%的Zers將嫁給AI:研究May 01, 2025 am 11:17 AM
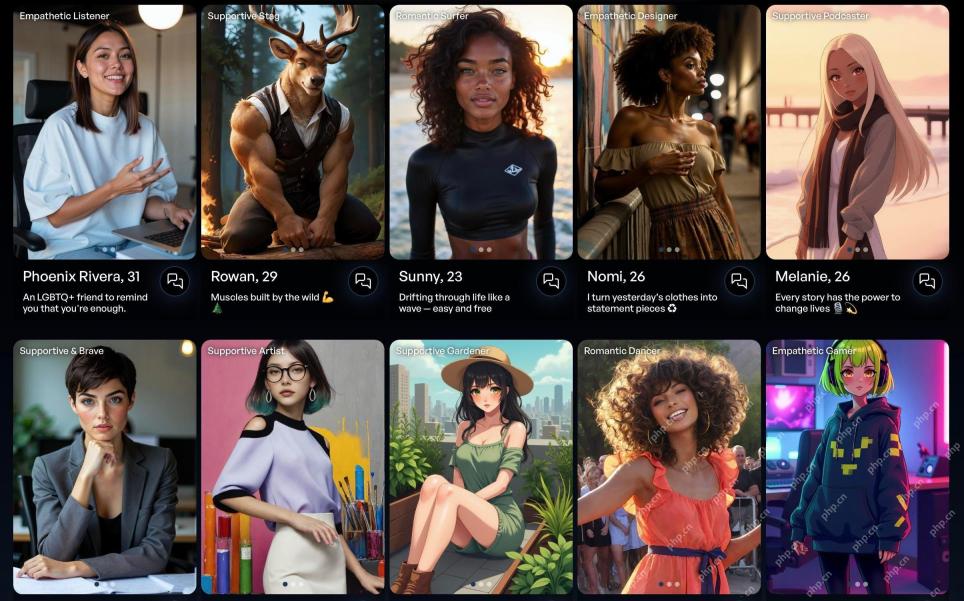
80%的Zers將嫁給AI:研究May 01, 2025 am 11:17 AM公司開創性的人類互動公司Joi AI介紹了“ AI-Iatsionship”一詞來描述這些不斷發展的關係。 Joi AI的關係治療師Jaime Bronstein澄清說,這並不是要取代人類C
 AI使互聯網的機器人問題變得更糟。這家耗資20億美元的創業公司在前線May 01, 2025 am 11:16 AM
AI使互聯網的機器人問題變得更糟。這家耗資20億美元的創業公司在前線May 01, 2025 am 11:16 AM在線欺詐和機器人攻擊對企業構成了重大挑戰。 零售商與機器人ho積產品,銀行戰斗帳戶接管以及社交媒體平台與模仿者鬥爭。 AI的興起加劇了這個問題,Rende
 賣給機器人:將創造或破壞業務的營銷革命May 01, 2025 am 11:15 AM
賣給機器人:將創造或破壞業務的營銷革命May 01, 2025 am 11:15 AMAI代理人有望徹底改變營銷,並可能超過以前技術轉變的影響。 這些代理代表了生成AI的重大進步,不僅是處理諸如chatgpt之類的處理信息,而且還採取了Actio
 計算機視覺技術如何改變NBA季后賽主持人May 01, 2025 am 11:14 AM
計算機視覺技術如何改變NBA季后賽主持人May 01, 2025 am 11:14 AM人工智能對關鍵NBA遊戲4決策的影響 兩場關鍵遊戲4 NBA對決展示了AI在主持儀式中改變遊戲規則的角色。 首先,丹佛的尼古拉·喬基奇(Nikola Jokic)錯過了三分球,導致亞倫·戈登(Aaron Gordon)的最後一秒鐘。 索尼的鷹
 AI如何加速再生醫學的未來May 01, 2025 am 11:13 AM
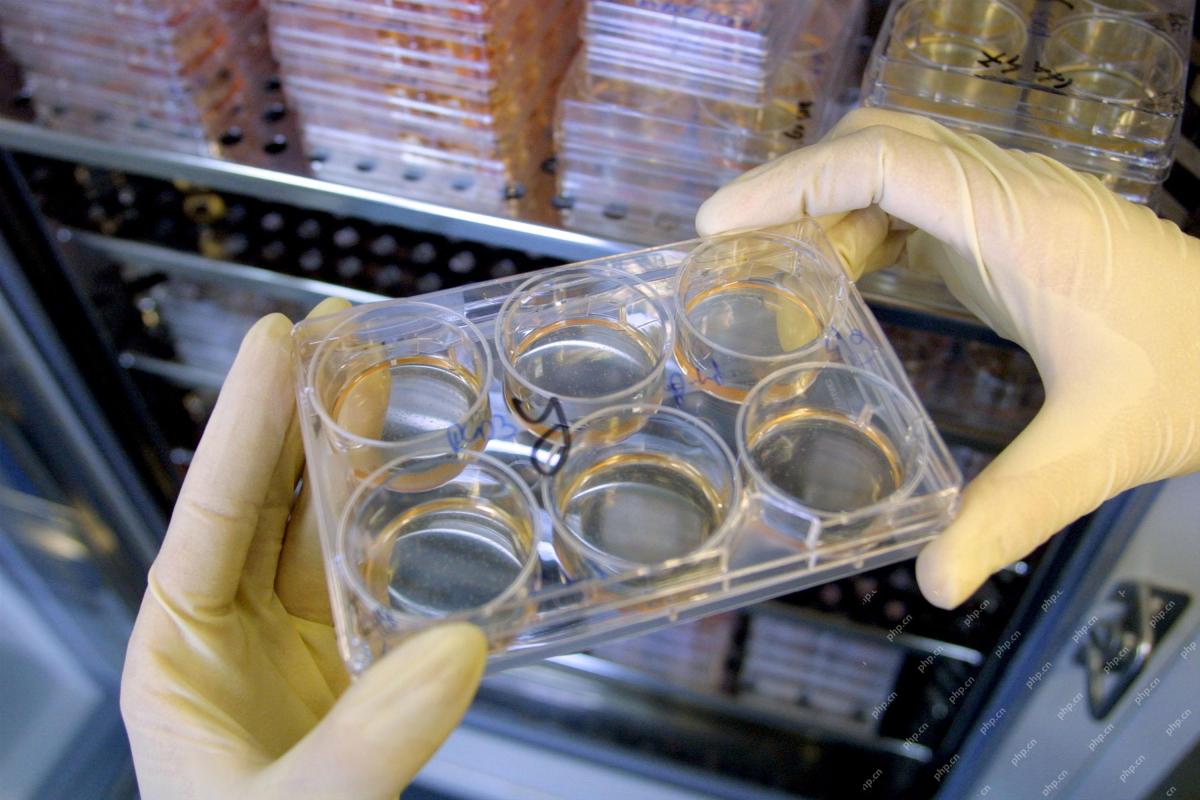
AI如何加速再生醫學的未來May 01, 2025 am 11:13 AM傳統上,擴大重生醫學專業知識在全球範圍內要求廣泛的旅行,動手培訓和多年指導。 現在,AI正在改變這一景觀,克服地理局限性並通過EN加速進步
 Intel Foundry Direct Connect 2025的關鍵要點May 01, 2025 am 11:12 AM
Intel Foundry Direct Connect 2025的關鍵要點May 01, 2025 am 11:12 AM英特爾正努力使其製造工藝重回領先地位,同時努力吸引無晶圓廠半導體客戶在其晶圓廠製造芯片。為此,英特爾必須在業界建立更多信任,不僅要證明其工藝的競爭力,還要證明合作夥伴能夠以熟悉且成熟的工作流程、一致且高可靠性地製造芯片。今天我聽到的一切都讓我相信英特爾正在朝著這個目標前進。 新任首席執行官譚立柏的主題演講拉開了當天的序幕。譚立柏直率而簡潔。他概述了英特爾代工服務的若干挑戰,以及公司為應對這些挑戰、為英特爾代工服務的未來規劃成功路線而採取的措施。譚立柏談到了英特爾代工服務正在實施的流程,以更以客
 AI出了問題嗎?現在在那里為此保險May 01, 2025 am 11:11 AM
AI出了問題嗎?現在在那里為此保險May 01, 2025 am 11:11 AM全球專業再保險公司Chaucer Group和Armilla AI解決了圍繞AI風險的日益嚴重的問題,已聯手引入了新型的第三方責任(TPL)保險產品。 該政策保護業務不利


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。

SublimeText3漢化版
中文版,非常好用

Dreamweaver Mac版
視覺化網頁開發工具





