
線性層是深度學習中最常用的層之一,在神經網路中扮演重要角色。它被廣泛應用於影像分類、物件偵測、語音辨識等任務。本文將重點放在線性層在多維張量上的作用。
首先,我們來回顧一下線性層的基本原理。對於一個輸入張量x,線性層的計算公式如下:
y=Wx b
其中,W和b分別是線性層的參數,W的形狀為(n_out, n_in),b的形狀為(n_out,)。 n_in表示輸入張量的大小,n_out表示輸出張量的大小。假設輸入張量是一個一維張量x∈R^n_in,輸出張量也是一個一維張量y∈R^n_out。在線性層中,輸入張量經過權重矩陣W的線性變換,再加上偏壓向量b,得到輸出張量y。這個線性變換可以表示為y = Wx b。其中,W的每一行代表了線性層的一個輸出神經元的權重向量,b的每一個元素表示了對應輸出神經元的偏移值。最終的輸出張量y的每一個元素都是透過對應的輸出神經元的權重向量和輸入張量進行點積,再加上對應的偏壓值得的。
現在,假設我們有一個多維張量X,它的形狀是(n_1,n_2,…,n_k)。我們需要將它傳遞給一個線性層,以產生一個輸出張量Y,它的形狀為(m_1,m_2,…,m_l)。這時,我們該怎麼做呢?
首先,我們需要將X展平成一維張量。這個過程通常被稱為「拉平」操作,可以使用PyTorch中的view函數來實現。具體地,我們可以將X的形狀變成(n_1\times n_2\times…\times n_k,),即將所有維度的元素都排成一列。這樣,我們就得到了一個一維張量x,它的大小是n_{in}=n_1\times n_2\times…\times n_k。
接下來,我們可以將x傳遞給線性層,得到輸出張量y。具體地,我們可以使用線性層的計算公式:
y=Wx b
這裡,W的形狀為(m_{out} ,n_{in}),b的形狀為(m_{out},),m_{out}表示輸出張量的大小。乘法Wx的結果是一個形狀為(m_{out},)的一維張量,加上偏置b後,得到形狀為(m_{out},)的輸出張量y。
最後,我們需要將y轉換回多維張量的形式。具體地,我們可以使用PyTorch中的view函數,將y的形狀變成(m_1,m_2,…,m_l)。這樣,我們就得到了最終的輸出張量Y。
要注意的是,在將多維張量展平成一維張量時,我們需要確保張量中的元素順序不變。例如,假設我們有一個形狀為(2,3)的二維張量X:
#X=\begin{bmatrix}1&2&3\4&5&6\end{bmatrix}
我們需要將它展平成一個一維張量。如果我們使用view(-1)來實現,得到的結果將會是:
x=[1,2,3,4,5,6]
#這裡,我們將(1,2)和(4,5)這兩行元素排在了一起,導致順序改變了。因此,正確的操作應該是使用view(-1)來展平張量,然後再使用view(1,-1)將其轉換回原來的形狀:
x =\begin{bmatrix}1&2&3&4&5&6\end{bmatrix}
X=\begin{bmatrix}1&2&3\4&5&6\end{bmatrix}
########################################################################################################################################################' #這樣,我們就可以正確地將多維張量傳遞給線性層,並且得到正確的輸出張量。 ############要注意的是,線性層在多維張量上的作用可以看作是對每個樣本進行獨立的線性變換。例如,假設我們有一個形狀為(N,C,H,W)的四維張量X,其中N表示樣本數,C表示通道數,H和W分別表示高度和寬度。我們可以將X沿著第一個維度(即樣本維度)展開成一個形狀為(N,C\times H\times W)的二維張量,然後將其傳遞給線性層。線性層會對每個樣本進行獨立的線性變換,得到形狀為(N,m_{out})的輸出張量Y。最後,我們可以將Y沿著第一個維度恢復成原來的形狀(N,m_1,m_2,…,m_l)。 ############總之,線性層在多維張量上的作用可以看作是對每個樣本進行獨立的線性變換。在實際應用中,我們通常會將多維張量展平成一維張量,然後將其傳遞給線性層。展平操作需要確保元素的順序不變,否則會導致計算結果錯誤。最後,我們需要將輸出張量恢復成原來的形狀,以便進行下一步計算。 ###以上是多維張量與線性層的交互原理是什麼?的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 特斯拉的Robovan是2024年的Robotaxi預告片中的隱藏寶石Apr 22, 2025 am 11:48 AM
特斯拉的Robovan是2024年的Robotaxi預告片中的隱藏寶石Apr 22, 2025 am 11:48 AM自2008年以來,我一直倡導這輛共享乘車麵包車,即後來被稱為“ Robotjitney”,後來是“ Vansit”,這是城市運輸的未來。 我預見這些車輛是21世紀的下一代過境解決方案Surpas
 Sam俱樂部在AI上押注以消除收據檢查並增強零售Apr 22, 2025 am 11:29 AM
Sam俱樂部在AI上押注以消除收據檢查並增強零售Apr 22, 2025 am 11:29 AM革新結帳體驗 Sam's Club的創新性“ Just Go”系統建立在其現有的AI驅動“掃描和GO”技術的基礎上,使會員可以在購物旅行期間通過Sam's Club應用程序進行掃描。
 Nvidia的AI Omniverse在GTC 2025擴展Apr 22, 2025 am 11:28 AM
Nvidia的AI Omniverse在GTC 2025擴展Apr 22, 2025 am 11:28 AMNVIDIA在GTC 2025上的增強可預測性和新產品陣容 NVIDIA是AI基礎架構的關鍵參與者,正在專注於提高其客戶的可預測性。 這涉及一致的產品交付,達到績效期望以及
 探索Google的功能Apr 22, 2025 am 11:26 AM
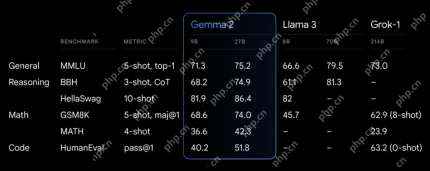
探索Google的功能Apr 22, 2025 am 11:26 AMGoogle的Gemma 2:強大,高效的語言模型 Google的Gemma語言模型家族以效率和性能而慶祝,隨著Gemma 2的到來而擴展。此最新版本包括兩種模型:270億個參數VER
 下一波《 Genai:與Kirk Borne博士的觀點》 -Analytics VidhyaApr 22, 2025 am 11:21 AM
下一波《 Genai:與Kirk Borne博士的觀點》 -Analytics VidhyaApr 22, 2025 am 11:21 AM這一領先的數據劇集以數據科學家,天體物理學家和TEDX演講者Kirk Borne博士為特色。 Borne博士是大數據,AI和機器學習的著名專家,為當前狀態和未來的Traje提供了寶貴的見解
 AI適合跑步者和運動員:我們取得了出色的進步Apr 22, 2025 am 11:12 AM
AI適合跑步者和運動員:我們取得了出色的進步Apr 22, 2025 am 11:12 AM這次演講中出現了一些非常有見地的觀點——關於工程學的背景信息,這些信息向我們展示了為什麼人工智能如此擅長支持人們的體育鍛煉。 我將從每位貢獻者的觀點中概括出一個核心思想,以展示三個設計方面,這些方面是我們探索人工智能在體育運動中應用的重要組成部分。 邊緣設備和原始個人數據 關於人工智能的這個想法實際上包含兩個組成部分——一個與我們放置大型語言模型的位置有關,另一個與我們人類語言和我們的生命體徵在實時測量時“表達”的語言之間的差異有關。 Alexander Amini 對跑步和網球都很了解,但他還
 傑米·恩格斯特羅姆(Jamie Engstrom)關於卡特彼勒的技術,人才和轉型Apr 22, 2025 am 11:10 AM
傑米·恩格斯特羅姆(Jamie Engstrom)關於卡特彼勒的技術,人才和轉型Apr 22, 2025 am 11:10 AM卡特彼勒(Caterpillar)的首席信息官兼高級副總裁傑米·恩格斯特(Jamie Engstrom)領導了一支由28個國家 /地區的2200多名IT專業人員組成的全球團隊。 在卡特彼勒(Caterpillar)工作了26年,其中包括她目前的四年半,Engst
 新的Google照片更新使任何具有Ultra HDR質量的照片流行Apr 22, 2025 am 11:09 AM
新的Google照片更新使任何具有Ultra HDR質量的照片流行Apr 22, 2025 am 11:09 AMGoogle Photos的新Ultra HDR工具:快速指南 使用Google Photos的新型Ultra HDR工具增強照片,將標準圖像轉換為充滿活力的高動態範圍傑作。對於社交媒體而言,此工具可提高任何照片的影響,


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

Safe Exam Browser
Safe Exam Browser是一個安全的瀏覽器環境,安全地進行線上考試。該軟體將任何電腦變成一個安全的工作站。它控制對任何實用工具的訪問,並防止學生使用未經授權的資源。

Atom編輯器mac版下載
最受歡迎的的開源編輯器

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。





