常用的距離度量方法在K最近鄰演算法的應用

k最近鄰演算法是一種用於分類和識別的基於實例或基於記憶體的機器學習演算法。它的原理是透過找到給定查詢點的最近鄰資料來進行分類。由於該演算法嚴重依賴已儲存的訓練數據，它可以被視為一個非參數化的學習方法。

k最近鄰演算法適用於處理分類或迴歸問題。對於分類問題，它使用離散值進行處理，而對於迴歸問題，它使用連續值進行處理。在進行分類之前，必須定義距離，常見的距離測量方法有多種選擇。

歐幾裡得距離

這是常用的距離量測，適用於實值向量。公式測量查詢點與另一點之間的直線距離。

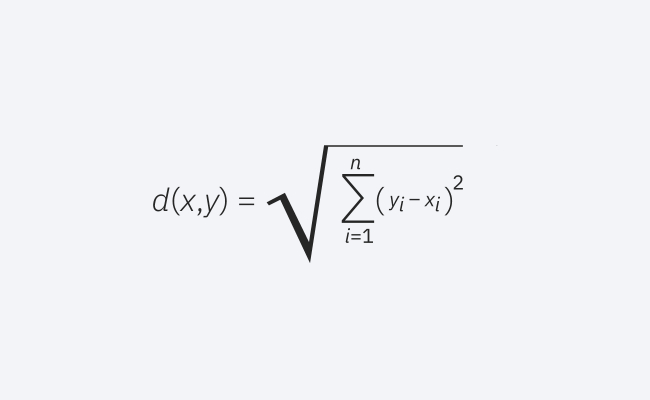
歐幾裡得距離公式

曼哈頓距離

這也是一種流行的距離度量，它測量兩點之間的絕對值。

曼哈頓距離公式

閔可夫斯基距離

此距離測量是歐幾里德和曼哈頓距離度量的廣義形式。

閔可夫斯基距離公式

漢明距離

該技術通常與布林或字串向量一起使用，識別向量不符的點。因此，它也被稱為重疊度量。

漢明距離公式

確定k最近鄰演算法距離的意義

為了確定哪些資料點最接近給定查詢點，需要計算查詢點與其他數據點之間的距離。這些距離測量有助於形成決策邊界，將查詢點劃分為不同的區域。

以上是常用的距離度量方法在K最近鄰演算法的應用的詳細內容。更多資訊請關注PHP中文網其他相關文章！