深入解析多元線性迴歸模型的概念與應用
- 王林轉載
- 2024-01-22 18:30:211699瀏覽
多元線性迴歸是最常見的線性迴歸形式,用來描述單一反應變數Y如何與多個預測變數呈現線性關係。
可以使用多重回歸的應用範例:
房子的售價可能受到地點、臥室和浴室數量、建造年份、地塊面積等因素的影響。
2、孩子的身高取決於母親的身高、父親的身高、營養和環境因素。
多元線性迴歸模型參數
考慮一個具有k個獨立預測變數x1、x2…、xk和一個反應變數y的多元線性迴歸模型。
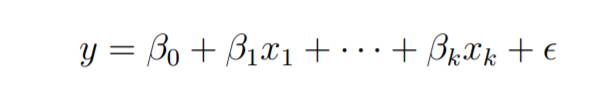
假設我們對k 1個變數有n個觀測值,且n的變數應該大於k。
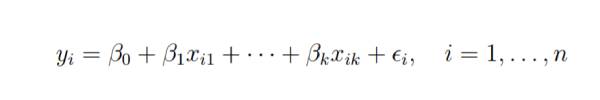
最小二乘迴歸的基本目標是將超平面擬合到(k 1)維空間中,以最小化殘差平方和。
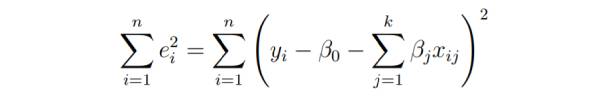
在對模型參數求導之前,將它們設為零並導出參數必須滿足的最小二乘法線方程式。
這些方程式是在向量和矩陣的幫助下制定的。

線性迴歸模型的寫法如下:
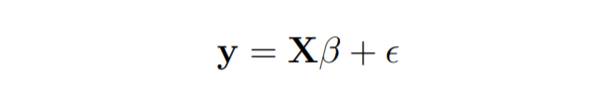 ##在線在性迴歸中,最小平方法參數估計b
##在線在性迴歸中,最小平方法參數估計b
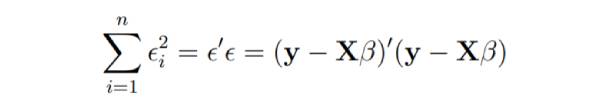 #想像X的列是固定的,它們是特定問題的數據,並且說b是可變的。我們希望找到殘差平方和最小化的“最佳”b。 平方和可能為零的最小值。
#想像X的列是固定的,它們是特定問題的數據,並且說b是可變的。我們希望找到殘差平方和最小化的“最佳”b。 平方和可能為零的最小值。
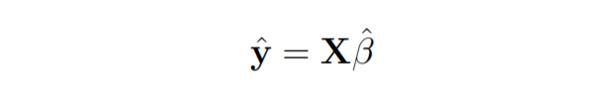 這裡y是估計的反應向量。 程式碼在資料集data2上實作多元線性迴歸data2資料集
這裡y是估計的反應向量。 程式碼在資料集data2上實作多元線性迴歸data2資料集
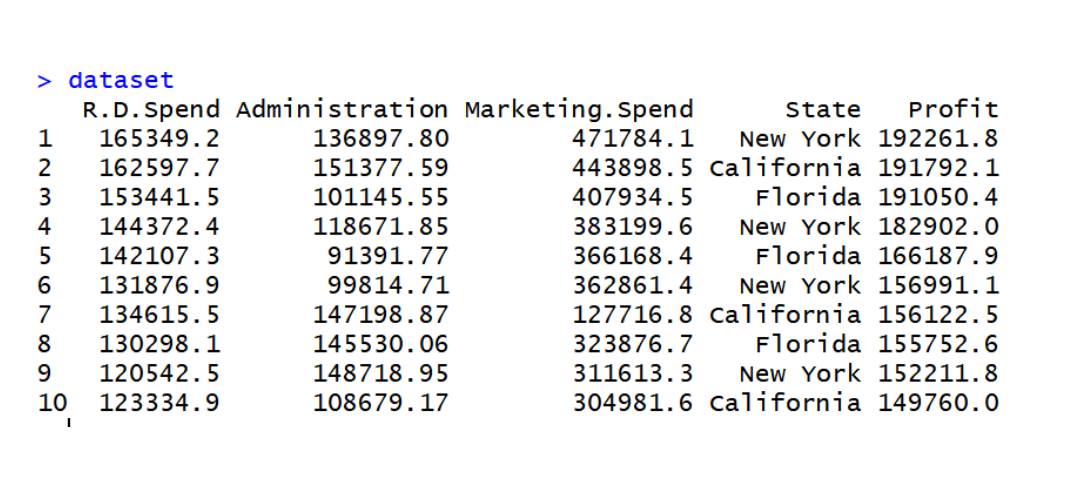
dataset=read.csv('data2.csv') dataset$State=factor(dataset$State, levels=c('New York','California','Florida'), labels=c(1,2,3)) dataset$State
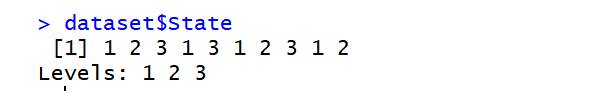
library(caTools) set.seed(123) split=sample.split(dataset$Profit,SplitRatio=0.8) training_set=subset(dataset,split==TRUE) test_set=subset(dataset,split==FALSE) regressor=lm(formula=Profit~., data=training_set) y_pred=predict(regressor,newdata=test_set)
以上是深入解析多元線性迴歸模型的概念與應用的詳細內容。更多資訊請關注PHP中文網其他相關文章!
陳述:
本文轉載於:163.com。如有侵權,請聯絡admin@php.cn刪除
上一篇:概念模型轉換為關係模型的深入解析下一篇:概念模型轉換為關係模型的深入解析

