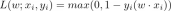1、簡介
生成式人工智慧無疑是一個改變遊戲規則的技術,但對於大多數商業問題來說,回歸和分類等傳統的機器學習模型仍然是首選。
重寫後的內容:設想一下私募股權或創投等投資者如何利用機器學習。要回答這個問題,首先需要了解投資人關注的數據以及數據的使用方式。投資公司的決策不僅基於可量化的數據,例如支出、成長和燒錢率等,還包括創辦人的記錄、客戶回饋和產品體驗等定性數據
本文將介紹線性回歸的基礎知識,可以在這裡找到完整的程式碼。
需要重寫的內容是:【程式碼】:https://github.com/RoyiHD/linear-regression
2、專案設定
本文將使用Jupyter Notebook進行這個專案。首先導入一些庫。
匯入庫
# 绘制图表import matplotlib.pyplot as plt# 数据管理和处理from pandas import DataFrame# 绘制热力图import seaborn as sns# 分析from sklearn.metrics import r2_score# 用于训练和测试的数据管理from sklearn.model_selection import train_test_split# 导入线性模型from sklearn.linear_model import LinearRegression# 代码注释from typing import List
3、資料
為了簡化問題,本文將使用區域資料。這些數據代表了公司的支出類別和利潤。可以看到一些不同數據點的範例。本文希望使用支出資料來訓練一個線性迴歸模型並預測利潤。
重要的是要理解本文所描述的數據是關於一家公司的支出情況。只有當將支出數據與收入成長、當地稅收、攤銷和市場狀況等數據結合時,才能得出有意義的預測能力
R&D Spend |
#行政管理 |
# #Marketing |
投資收益 |
| #需要重寫的內容是:165349.2 |
136897.8 |
#需要重寫的內容是:471784.1 |
#需要改寫的內容是:192261.83 |
| #162597.7 |
#需要被重寫的內容是:151377.59 |
443898.53 |
|
153441.51 |
101145.55 |
加载数据
companies: DataFrame = pd.read_csv("companies.csv", header = 0)
4、数据可视化
了解数据对于确定要使用的特征、需要进行归一化和转换的特征、从数据中删除异常值以及对特定数据点进行的处理是很重要的。
目标(利润)直方图
可以直接使用DataFrame绘制直方图(Pandas使用Matplotlib来绘制数据帧),可以直接访问利润并绘制它。
companies['Profit'].hist( color='g', bins=100);
 图片
图片
从数据中可以清楚地看出,利润超过20万美元的异常值非常罕见。这表明本文所涉及的数据代表的是规模较大的公司。鉴于异常值数量较少,可以将其保留
特征(支出)直方图
在这里,本文旨在使用特征的直方图,并观察其分布情况。Y轴表示数字频率,X轴表示支出
companies[["R&D Spend", "行政管理", "Marketing Spend"]].hist(figsize=(16, 20), bins=50, xlabelsize=8, ylabelsize=8)
 图片
图片
可以观察到一个健康的分布,只有很少的异常值。根据直觉,可以预期投入更多资金在研发和市场营销上的公司会获得更高的利润。从下面的散点图中可以看出,研发支出和利润之间存在明显的相关性
profits: DataFrame = companies[["Profit"]]research_and_development_spending: DataFrame = companies[["R&D Spend"]]figure, ax = plt.subplots(figsize = (9, 9))plt.xlabel("R&D Spending")plt.ylabel("Profits")ax.scatter(research_and_development_spending, profits, s=60, alpha=0.7, edgecolors="k",color='g',linewidths=0.5)
 图片
图片
可以使用相关的热图来进一步探索支出和利润之间的关系。从图中可以观察到研发和市场营销支出与利润之间的相关性比行政支出更高
sns.heatmap(companies.corr())
 图片
图片
5、模型训练
首先需要将数据集分割为训练集和测试集两部分。Sklearn提供了一个辅助方法来完成这个任务。鉴于本文的数据集很简单且足够小,可以按照以下方式将特征和目标分离开来。
数据集
features: DataFrame = companies[["R&D Spend", "行政管理", "Marketing Spend",]]targets: DataFrame = companies[["Profit"]]train_features, test_features, train_targets, test_targets = train_test_split(features, targets,test_size=0.2)
大多数数据科学家会使用不同的命名约定,如X_train、y_train或其他类似的变体。
模型训练
现在可以创建并训练模型了。Sklearn使事情变得非常简单。
model: LinearRegression = LinearRegression()model.fit(train_features, train_targets)
6、模型评估
本文希望对模型的性能及其可用性进行评估。首先查看一下计算得到的系数。在机器学习中,系数是用来与每个特征相乘的学习到的权重或数值。期望看到每个特征都有一个学习系数。
coefficients = model.coef_"""We should see the following in our consoleCoefficients[[0.55664299 1.08398919 0.07529883]]"""
正如上述所看到的,有3个系数,每个特征对应一个系数(“研发支出”、“行政支出”、“市场营销支出”)。还可以将其绘制成图表,以便更直观地了解每个系数。
plt.figure()plt.barh(train_features.columns, coefficients[0])plt.show()
 图片
图片
计算误差
希望了解模型的误差率,我们将使用Sklearn的R2得分
test_predictions: List[float] = model.predict(test_features)root_squared_error: float = r2_score(test_targets, test_predictions)"""floatWe should see an ouput similar to this0.9781424529214315"""
离1越近,模型就越准确。实际上可以用一种非常简单的方式对这一点进行测试。
使用下面的支出模型来预测利润,并希望得到一个接近192261美元的数字,可以提取数据集的第一行
"R&D Spend" |"行政管理" |"Marketing Spend" | "Profit"需要进行重写的内容是:165349.2 136897.8需要重写的内容是:471784.1需要改写的内容是:192261.83
接下来创建一个推理请求。
inference_request: DataFrame = pd.DataFrame([{"R&D Spend":需要进行重写的内容是:165349.2, "行政管理":136897.8, "Marketing Spend":需要重写的内容是:471784.1 }])
运行模型。
inference: float = model.predict(inference_request)"""We should get a number that is around199739.88721901"""
现在可以看到的误差率是abs(199739-192261)/192261=0.0388。这是非常准确的。
7、结论
处理数据、搭建模型和分析数据有很多方法。没有一种解决方案适用于所有情况,当用机器学习解决业务问题时,其中一个关键过程是搭建多个旨在解决同一个问题的模型,并选择最有前途的模型
以上是利潤預測不再困難,scikit-learn線性迴歸法讓你事半功倍的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM
優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM介紹 恭喜!您經營一家成功的業務。通過您的網頁,社交媒體活動,網絡研討會,會議,免費資源和其他來源,您每天收集5000個電子郵件ID。下一個明顯的步驟是
 Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM
Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM介紹 在當今快節奏的軟件開發環境中,確保最佳應用程序性能至關重要。監視實時指標,例如響應時間,錯誤率和資源利用率可以幫助MAIN
 Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM“您有幾個用戶?”他扮演。 阿爾特曼回答說:“我認為我們上次說的是每週5億個活躍者,而且它正在迅速增長。” “你告訴我,就像在短短幾週內翻了一番,”安德森繼續說道。 “我說那個私人
 pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介紹 Mistral發布了其第一個多模式模型,即Pixtral-12b-2409。該模型建立在Mistral的120億參數Nemo 12B之上。是什麼設置了該模型?現在可以拍攝圖像和Tex
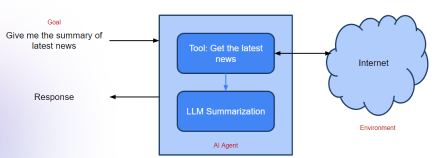 生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想像一下,擁有一個由AI驅動的助手,不僅可以響應您的查詢,還可以自主收集信息,執行任務甚至處理多種類型的數據(TEXT,圖像和代碼)。聽起來有未來派?在這個a


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

WebStorm Mac版
好用的JavaScript開發工具

禪工作室 13.0.1
強大的PHP整合開發環境

DVWA
Damn Vulnerable Web App (DVWA) 是一個PHP/MySQL的Web應用程序,非常容易受到攻擊。它的主要目標是成為安全專業人員在合法環境中測試自己的技能和工具的輔助工具,幫助Web開發人員更好地理解保護網路應用程式的過程,並幫助教師/學生在課堂環境中教授/學習Web應用程式安全性。 DVWA的目標是透過簡單直接的介面練習一些最常見的Web漏洞,難度各不相同。請注意,該軟體中

Atom編輯器mac版下載
最受歡迎的的開源編輯器

Dreamweaver CS6
視覺化網頁開發工具