中科大開發「狀態序列頻域預測」方法，效能提升20%，樣本效率達最大

強化學習演算法（Reinforcement Learning, RL）的訓練過程通常需要大量的與環境互動的樣本資料來支援。然而，在現實世界中，收集大量互動樣本往往非常昂貴，或無法確保採樣過程的安全性，例如無人機空戰訓練和自動駕駛訓練。這個問題限制了強化學習在許多實際應用中的應用範圍。因此，研究人員一直在努力探索如何在樣本效率和安全性之間取得平衡，以解決這個問題。一種可能的解決方法是使用模擬器或虛擬環境來產生大量的樣本數據，從而避免了實際世界中的成本和安全風險。另外，還有

為了提高強化學習演算法在訓練過程中的樣本效率，一些研究者利用表徵學習技術設計了預測未來狀態訊號的輔助任務。透過這種方式，演算法可以從原始的環境狀態中提取與未來決策相關的特徵進行編碼。這種方法的目的是透過學習更多有關環境的信息，提供更好的決策依據，從而改善強化學習演算法的表現。如此一來，演算法在訓練過程中可以更有效率地利用樣本數據，加速學習過程，提高決策的準確性和效率。

基於這個思路，該工作設計了一種預測未來多步驟的狀態序列頻域分佈的輔助任務，以捕捉更長遠的未來決策特徵，進而提升演算法的樣本效率。

此作品標題為State Sequences Prediction via Fourier Transform for Representation Learning，發表於NeurIPS 2023，並被接收為Spotlight。

作者表：葉鳴軒，匡宇飛，王傑*，楊睿，周文罡，李厚強，吳楓

#論文連結：https://openreview.net/forum?id=MvoMDD6emT

程式碼連結：https://github.com/MIRALab-USTC/RL-SPF /

研究背景與動機

深度強化學習演算法在機器人控制[1]、遊戲智慧[2]、組合最佳化[3 ]等領域取得了巨大的成功。但是，目前的強化學習演算法仍存在著「樣本效率低」的問題，即機器人需要大量與環境互動的數據才能訓得表現優異的策略。

為了提高樣本效率，研究人員開始專注於表徵學習，希望透過訓練得到的表徵能夠從環境的原始狀態中提取出豐富而有用的特徵信息，從而提高機器人在狀態空間中的探索效率。

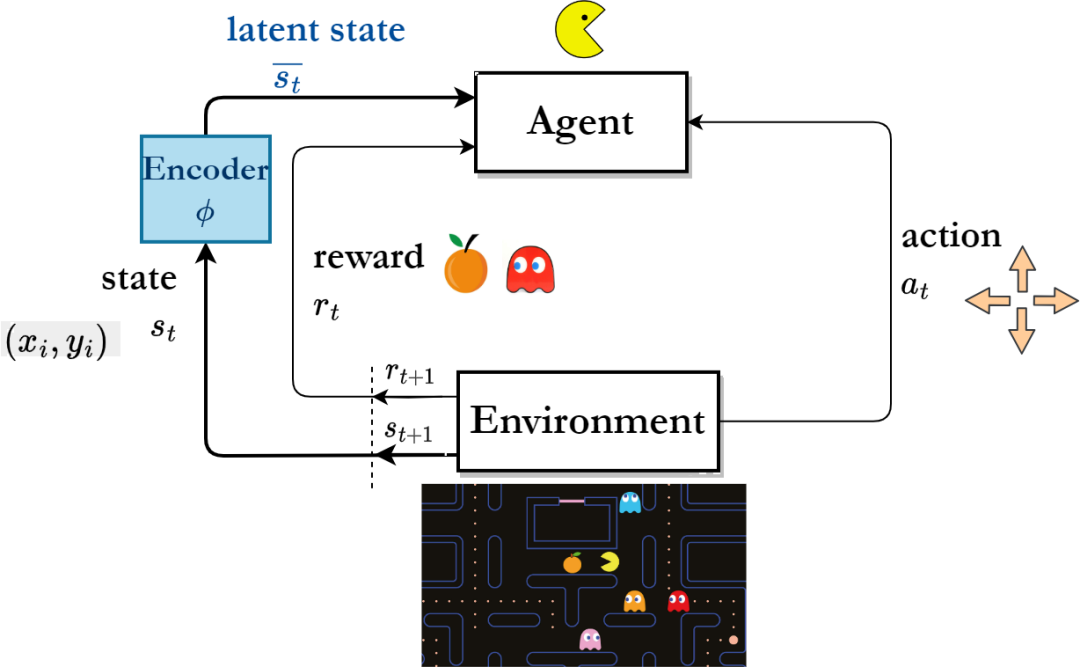
基於表徵學習的強化學習演算法框架

在序列決策任務中， 「長期的序列訊號」相對於單步驟訊號包含更多有利於長期決策的未來資訊。啟發於此觀點，一些研究者提出透過預測未來多步驟的狀態序列訊號來輔助表徵學習[4,5]。然而，直接預測狀態序列來輔助表徵學習是非常困難的。

現有的兩類方法中，一類方法透過學習單步驟機率轉移模型來逐步地產生單一時刻的未來狀態，以間接預測多步的狀態序列[6,7]。但是，這類方法對所訓練的機率轉移模型的精度要求很高，因為每步的預測誤差會隨預測序列長度的增加而累積。

另一類方法透過直接預測未來多步驟的狀態序列來輔助表徵學習[8]，但這類方法需要儲存多個步驟的真實狀態序列作為預測任務的標籤，所耗儲存量大。因此，如何有效從環境的狀態序列中提取有利於長期決策的未來訊息，進而提升連續控制機器人訓練時的樣本效率是需要解決的問題。

為了解決上述問題，我們提出了一個基於狀態序列頻域預測的表徵學習方法（State Sequences Prediction via Fourier Transform, SPF），其想法是利用「狀態序列的頻域分佈」來明確提取狀態序列資料中的趨勢性與規律性訊息，從而輔助表徵有效率地擷取到長期未來資訊。

狀態序列中的結構性資訊分析

我們從理論上證明了狀態序列存在「兩個結構性資訊」，一是與策略表現相關的趨勢性訊息，二是與狀態週期性相關的規律性資訊。

馬爾科夫決策過程

在具體分析兩個結構性資訊之前，我們先介紹產生狀態序列的馬爾科夫決策過程（Markov Decision Processes，MDP）的相關定義。

我們考慮連續控制問題中的經典馬可夫決策過程，該過程可用五元組  表示。其中， 為對應的狀態、動作空間， 為獎勵函數， 為環境的狀態轉移函數， 為狀態的初始分佈， 為折扣因子。此外，我們用  表示策略在狀態  下的動作分佈。

我們將  時刻下智能體所處的狀態記為 ，所選的動作記為 .智能體做出動作後，環境轉移到下一時刻狀態  並回饋給智能體獎勵 。我們將智能體與環境互動過程中所得到狀態、動作對應的軌跡記為 ，軌跡服從分佈 。

強化學習演算法的目標是最大化未來預期的累積回報，我們用  表示目前策略  和環境模式  下的平均累積回報，簡稱為  ，並定義如下：

 顯示了目前策略  的效能表現。

趨勢性資訊

下面我們介紹狀態序列的「第一種結構性特徵」，其涉及狀態序列與對應獎勵序列之間的依賴關係，能顯示出目前策略的效能趨勢。

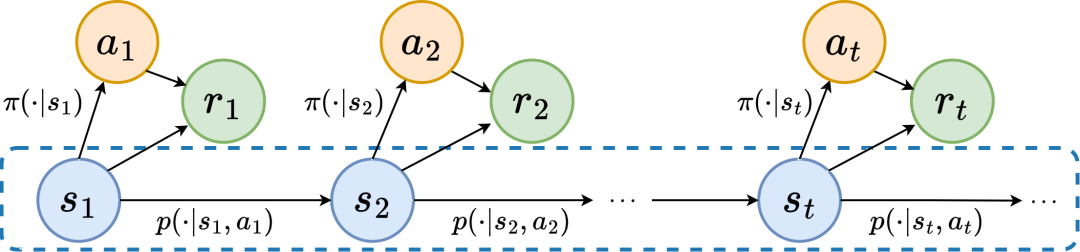
在強化學習任務中，未來的狀態序列很大程度上決定了智能體未來採取的動作序列，並進一步決定了相應的獎勵序列。因此，未來的狀態序列不僅包含環境固有的機率轉移函數的訊息，也能輔助表徵捕捉反映當前策略的走向趨勢。

啟發上述結構，我們證明了以下定理，進一步論證了這個結構性依賴關係的存在：

定理一：若獎勵函數只與狀態有關，那麼對於任兩個策略  和 ，他們的表現差異可以被這兩個策略所產生的狀態序列分佈差異所控制：

在上述公式中， 表示在指定策略和轉移機率函數條件下狀態序列的機率分佈， 表示  範數。

上述定理表明，兩個策略的表現差異越大，其對應的兩個狀態序列的分佈差異就越大。這意味著好策略和壞策略會產生兩個差異較大的狀態序列，這進一步說明狀態序列所包含的長期結構性資訊能潛在影響搜尋表現優異的策略的效率。

另一方面，在一定條件下，狀態序列的頻域分佈差異也能為對應的策略效能差異提供上界，具體如以下定理所示：

定理二：若狀態空間有限維度且獎勵函數是與狀態有關的n次多項式，那麼對於任兩個策略  和 ，他們的表現差異可以被這兩個策略所產生的狀態序列的頻域分佈差異所控制：

上述公式中， 表示由策略  產生的狀態序列的  次方序列的傅立葉函數，表示傅立葉函數的第  個分量。

這個定理顯示狀態序列的頻域分佈仍包含與目前策略效能相關的特徵。

規律性資訊

下面我們介紹狀態序列中存在的「第二種結構性特徵」，其涉及狀態訊號之間的時間依賴性，即一段較長時期內狀態序列所表現出的規律性模式。

在許多的真實場景任務中，智能體也會表現出週期性行為，因為其環境的狀態轉移函數本身就是具有週期性的。以工業組裝機器人為例，該機器人的訓練目標是將零件組裝在一起以創造最終產品，當策略訓練達到穩定時，它就會執行一個週期性的動作序列，使其能夠有效地將零件組裝在一起。

啟發於上面的例子，我們提供了一些理論分析，證明了有限狀態空間中，當轉移機率矩陣滿足某些假設，對應的狀態序列在智能體達到穩定策略時可能表現出「漸近週期性」，具體定理如下：

#定理三：對於狀態轉移矩陣為  的有限維狀態空間 ，假設  有  個循環類，對應的狀態轉移子矩陣為 。設此  個矩陣模為1的特徵值個數為 ，則對於任意狀態的初始分佈 ，狀態分佈  呈現週期為  的漸進週期性。

在MuJoCo任務中，策略訓練達到穩定時，智能體也會表現出週期性的動作。下圖中給出了MuJoCo任務中HalfCheetah智能體在一段時間內的狀態序列範例，可以觀察到明顯的週期性。 （更多MuJoCo任務中帶週期性的狀態序列範例可參考本論文附錄第E節）

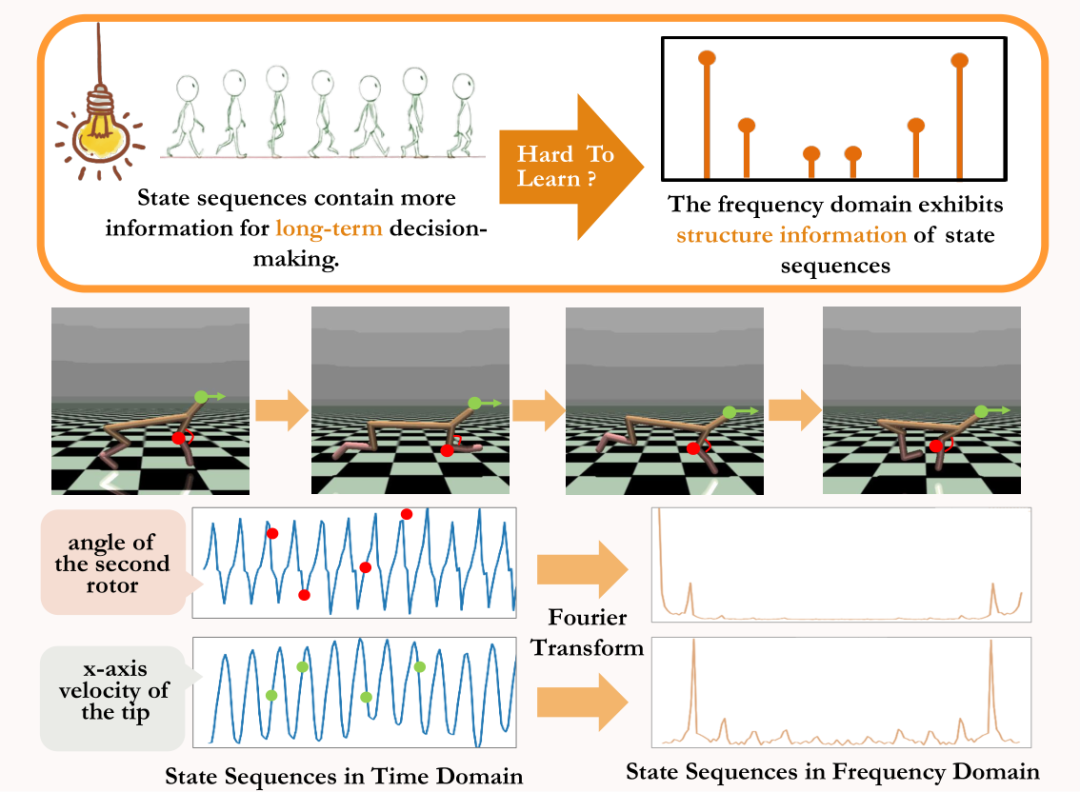
#MuJoCo任務中HalfCheetah智能體在一段時間內狀態所表現出的週期性

時間序列在時域中呈現的資訊相對分散，但在頻域中，序列中的規律性資訊以更集中的形式呈現。透過分析頻域中的頻率分量，我們能明確地捕捉到狀態序列中存在的週期性特徵。

方法介紹

上一個部分中，我們從理論上證明狀態序列的頻域分佈能反映策略性能的好壞，並且透過在頻域上分析頻率分量我們能明確地捕捉到狀態序列中的週期性特徵。

啟發於上述分析，我們設計了「預測無窮步未來狀態序列傅立葉變換」的輔助任務來鼓勵表徵提取狀態序列中的結構性資訊。

SPF方法損失函數

以下介紹我們關於該輔助任務的建模。給定目前狀態  與動作 ，我們定義未來的狀態序列期望如下：

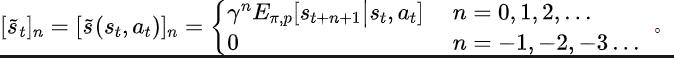
#我們的輔助任務訓練表徵去預測上述狀態序列所期望的離散時間傅立葉轉換（discrete-time Fourier transform, DTFT），即

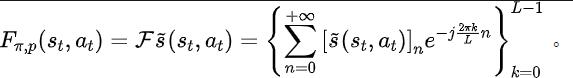
上述傅立葉轉換公式可改寫為如下的遞歸形式：

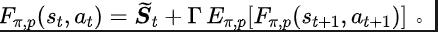
#其中，

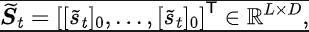
其中， 為狀態空間的維度， 為所預測的狀態序列傅立葉函數的離散化點的數量。

啟發於Q-learning中最佳化Q值網路的TD-error損失函數[9]，我們設計如下的損失函數：

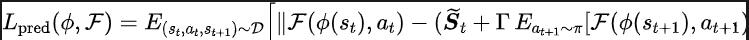
其中， 和  分別為損失函數要最佳化的表徵編碼器（encoder）和傅立葉函數預測器（predictor）的神經網路參數， 為儲存樣本資料的經驗池。

進一步地，我們可以證明上述的遞迴公式可以表示為一個壓縮映射：

##定理四：令  表示函數族 ，定義  上的範數為：

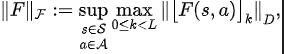
其中  表示矩陣  的第  行向量。我們定義映射  為

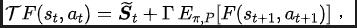
則可以證明  為壓縮對應。

根據壓縮映射原理，我們可以迭代地使用算符 ，使得  逼近真實狀態序列的頻域分佈，且在表格型情況（tabular setting）下有收斂性保證。

此外，我們所設計的損失函數只依賴當下時刻與下一時刻的狀態，所以無需儲存未來多步驟的狀態資料作為預測標籤，具有“實作簡單且儲存量低”的優點。

SPF方法演算法框架

下面我們介紹本論文方法（SPF）的演算法框架。

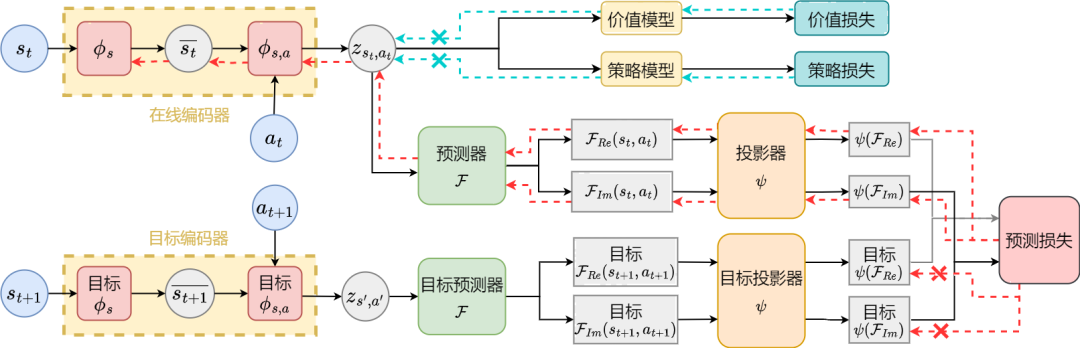基於狀態序列頻域預測的表徵學習方法（SPF）的演算法框架圖

我們將當下時刻和下一時刻的狀態-動作數據分別輸入到線上（online）和目標（target）表徵編碼器（encoder）中，得到狀態-動作表徵數據，然後將該表徵數據輸入到傅立葉函數預測器（predictor）得到當下時刻和下一時刻下的兩組狀態序列傅立葉函數預測值。透過代入這兩組傅立葉函數預測值，我們能計算出損失函數值。

我們透過最小化損失函數來最佳化更新表徵編碼器  和傅立葉函數預測器 ，使預測器的輸出能逼近真實狀態序列的傅立葉變換，從而鼓勵表徵編碼器提取出包含未來長期狀態序列的結構性資訊的特徵。

我們將原始狀態和動作輸入到表徵編碼器中，將得到的特徵作為強化學習演算法中actor網絡和critic網絡的輸入，並用經典強化學習演算法優化actor網絡和critic網。

實驗結果

（註：本節僅選取部分實驗結果，更詳細的結果請參考論文原文第6節及附錄。）

演算法效能比較

我們將SPF 方法在MuJoCo 模擬機器人控制環境上測試，對如下6 種方法進行比較：

• SAC：基於Q值學習的soft actor-critic演算法[10]，一種傳統的RL演算法；
• PPO：基於策略最佳化的proximal policy optimization演算法[11]，一種傳統RL演算法；
• SAC-OFE :利用預測單步驟未來狀態的輔助任務進行表徵學習，以最佳化SAC演算法；
• PPO-OFE:利用預測單步未來狀態的輔助任務進行表徵學習，以最佳化PPO演算法；
• SAC-SPF:利用預測無窮步狀態序列的頻域函數的輔助任務進行表徵學習（我們的方法），以最佳化SAC演算法；
• PPO-SPF:利用預測無窮步狀態序列的頻域函數的輔助任務進行表徵學習（我們的方法），以最佳化PPO演算法；

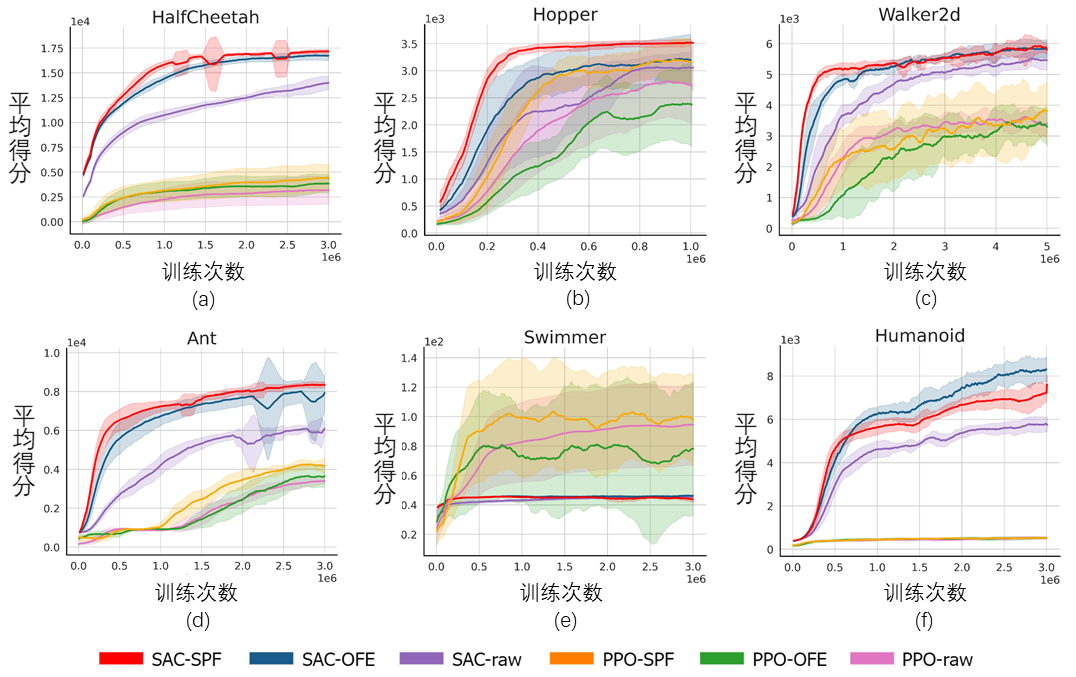
#基於6種MuJoCo任務的比較實驗結果

上圖顯示了在 6 種 MuJoCo 任務中，我們所提出的SPF方法（紅線及橙線）與其他對比方法的效能曲線。結果顯示，我們所提出的方法相比於其他方法能獲得19.5%的效能提升。

消融實驗

我們對SPF 方法的各個模組進行了消融實驗，將本方法與不使用投影模組（noproj） 、不使用目標網路模組（notarg）、改變預測損失（nofreqloss）、改變特徵編碼器網路結構（mlp，mlp_cat）時的效能表現做比較。

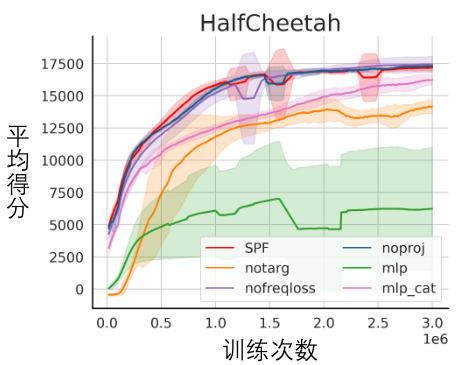
SPF方法應用於SAC演算法的消融實驗結果圖，測試於HalfCheetah任務

視覺化實驗

我們使用SPF 方法所訓練好的預測器輸出狀態序列的傅立葉函數，並透過逆傅立葉變換恢復出的200步狀態序列，與真實的200步狀態序列進行比較。

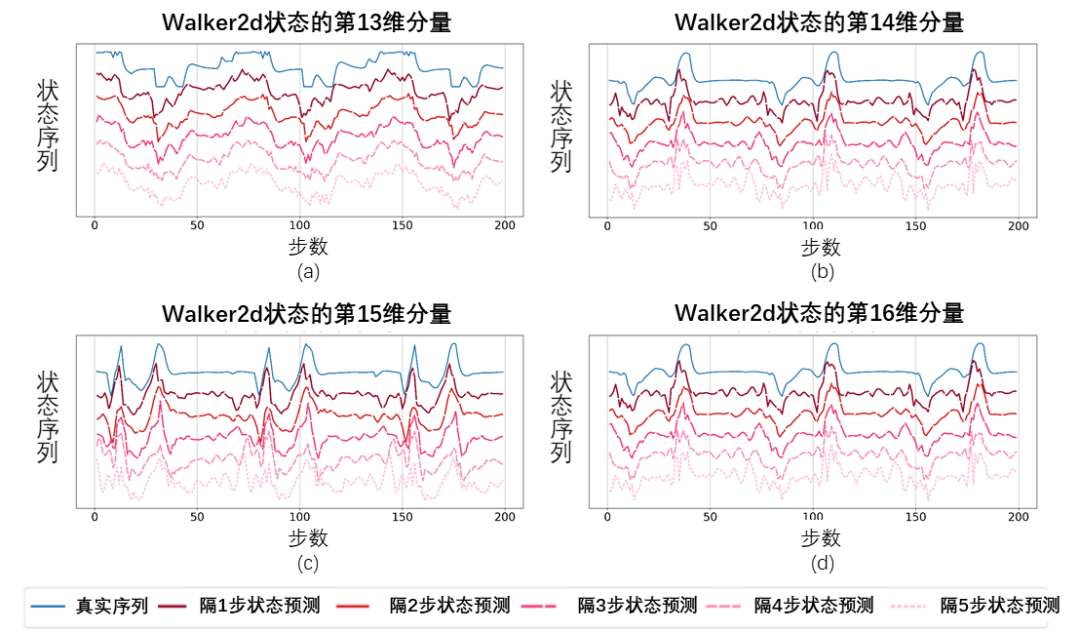基於傅立葉函數預測值恢復出的狀態序列示意圖，測試於Walker2d任務。其中，藍線為真實的狀態序列示意圖，5條紅線為恢復出的狀態序列示意圖，越下方的、顏色越淺的紅線表示利用越久遠的歷史狀態所恢復出的狀態序列。

結果顯示，即使用更久遠的狀態作為輸入，恢復的狀態序列也和真實的狀態序列非常相似，這說明SPF 方法所學習出的表徵能有效編碼出狀態序列中所包含的結構性資訊。

以上是中科大開發「狀態序列頻域預測」方法，效能提升20%，樣本效率達最大的詳細內容。更多資訊請關注PHP中文網其他相關文章！