確定資料分佈常態性的11種基本方法
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB轉載
- 2023-12-14 20:50:541597瀏覽
在資料科學和機器學習領域,許多模型都假設資料呈現常態分佈,或假設資料在常態分佈下表現較好。例如,線性迴歸假設殘差呈常態分佈,線性判別分析(LDA)基於常態分佈等假設進行推導。因此,了解如何測試資料常態性的方法對於資料科學家和機器學習從業者至關重要

#本篇文章旨在介紹11種基本方法來測試數據的常態性,以幫助讀者更好地了解資料分佈的特徵,並學會如何應用適當的方法進行分析。這樣可以更好地處理資料分佈對模型效能的影響,在機器學習與資料建模過程中更加得心應手
#繪圖法Plotting Methods
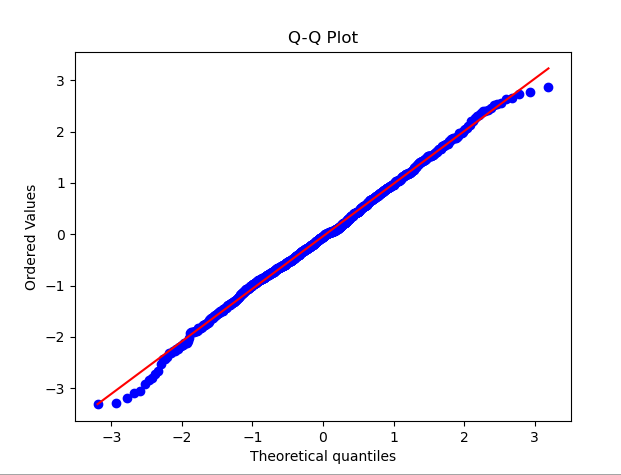
1.QQ Plot
QQ圖(分位數-分位數圖)是一種廣泛使用的方法,用於檢查資料分佈是否符合常態分佈。在QQ圖中,將資料的分位數與標準常態分佈的分位數進行比較,如果資料分佈接近常態分佈,則QQ圖上的點將接近一條直線
為了示範QQ圖,下面的範例程式碼產生了一組服從常態分佈的隨機資料。運行程式碼後,您可以看到QQ圖以及對應的常態分佈曲線。透過觀察圖上點的分佈情況,可以初步判斷資料是否接近常態分佈
import numpy as npimport scipy.stats as statsimport matplotlib.pyplot as plt# 生成一组随机数据,假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制QQ图stats.probplot(data, dist="norm", plot=plt)plt.title('Q-Q Plot')plt.show()
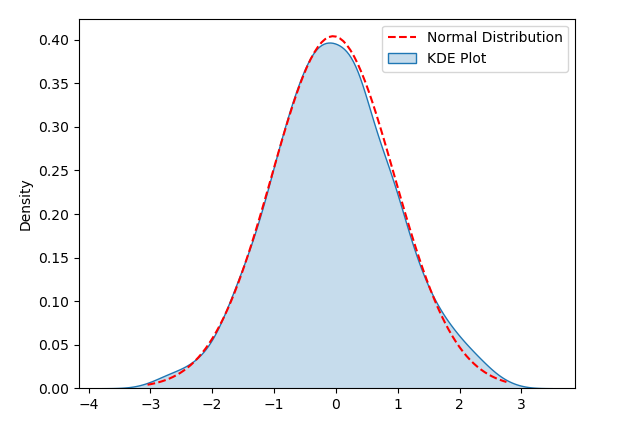
#2.KDE Plot
KDE(核密度估計)圖是一種用於視覺化資料分佈的方法,能夠幫助我們偵測資料的常態性。在KDE圖中,透過估計資料的密度並繪製成一條平滑的曲線,有助於我們觀察資料的分佈形狀
為了示範KDE Plot,下面的範例程式碼產生了一組服從常態分佈的隨機數據。運行程式碼後,您可以看到KDE Plot以及對應的常態分佈曲線,透過視覺化來偵測資料分佈是否符合常態性
import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=1000)# 创建KDE Plotsns.kdeplot(data, shade=True, label='KDE Plot')# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()
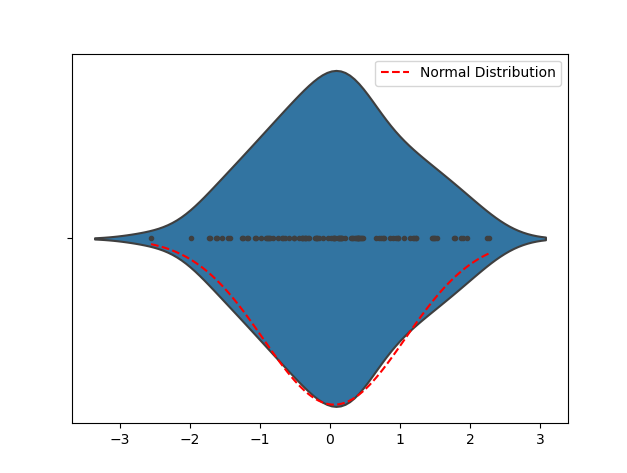
import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=100)# 创建 Violin Plotsns.violinplot(data, inner="points")# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()
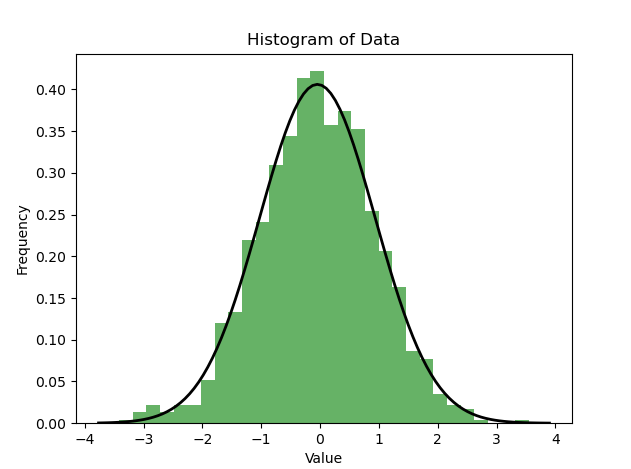
import numpy as npimport matplotlib.pyplot as pltimport scipy.stats as stats# 生成一组随机数据,假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制直方图plt.hist(data, bins=30, density=True, alpha=0.6, color='g')plt.title('Histogram of Data')plt.xlabel('Value')plt.ylabel('Frequency')# 绘制正态分布的概率密度函数xmin, xmax = plt.xlim()x = np.linspace(xmin, xmax, 100)p = stats.norm.pdf(x, np.mean(data), np.std(data))plt.plot(x, p, 'k', linewidth=2)plt.show()
- 統計量W:基於觀測資料與在常態分佈下的期望值之間的相關性來計算統計量W ,W的取值範圍在0和1之間,當W接近1時,表示觀測資料與常態分佈的擬合程度較好。
- P值:P值表示觀測到這種相關性的可能性,如果P值大於顯著水準(通常為0.05),則表示觀測資料很可能來自常態分佈。
from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk检验stat, p = stats.shapiro(data)print('Shapiro-Wilk Statistic:', stat)print('P-value:', p)# 根据P值判断正态性alpha = 0.05if p > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

6.KS检验
KS检验(Kolmogorov-Smirnov检验)是一种用于检验数据是否符合特定分布(例如正态分布)的统计方法。它通过计算观测数据与理论分布的累积分布函数(CDF)之间的最大差异来评估它们是否来自同一分布。其基本步骤如下:
- 对两个样本数据进行排序。
- 计算两个样本的经验累积分布函数(ECDF),即计算每个值在样本中的累积百分比。
- 计算两个累积分布函数之间的差异,通常使用KS统计量衡量。
- 根据样本的大小和显著性水平,使用参考表活计算p值判断两个样本是否来自同一分布。
Python中使用KS检验来检验数据是否符合正态分布时,可以使用Scipy库中的kstest函数。下面是一个简单的示例,演示了如何使用Python进行KS检验来检验数据是否符合正态分布。
from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行KS检验statistic, p_value = stats.kstest(data, 'norm')print('KS Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

7.Anderson-Darling检验
Anderson-Darling检验是一种用于检验数据是否来自特定分布(例如正态分布)的统计方法。它特别强调观察值在分布尾部的差异,因此在检测极端值的偏差方面非常有效
下面的代码使用stats.anderson函数执行Anderson-Darling检验,并获取检验统计量、临界值以及显著性水平。然后通过比较统计量和临界值,可以判断样本数据是否符合正态分布
from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Anderson-Darling检验result = stats.anderson(data, dist='norm')print('Anderson-Darling Statistic:', result.statistic)print('Critical Values:', result.critical_values)print('Significance Level:', result.significance_level)# 判断正态性if result.statistic <p style="text-align:center;"><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/170255826239547.png" class="lazy" alt="確定資料分佈常態性的11種基本方法"></p><h4>8.Lilliefors检验</h4><p>Lilliefors检验(也被称为Kolmogorov-Smirnov-Lilliefors检验)是一种用于检验数据是否符合正态分布的统计检验方法。它是Kolmogorov-Smirnov检验的一种变体,专门用于小样本情况。与K-S检验不同,Lilliefors检验不需要假定数据的分布类型,而是基于观测数据来评估是否符合正态分布</p><p>在下面的例子中,我们使用lilliefors函数进行Lilliefors检验,并获得了检验统计量和P值。通过将P值与显著性水平进行比较,我们可以判断样本数据是否符合正态分布</p><pre class="brush:php;toolbar:false">import numpy as npfrom statsmodels.stats.diagnostic import lilliefors# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Lilliefors检验statistic, p_value = lilliefors(data)print('Lilliefors Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')
9.距离测量Distance Measures
距离测量(Distance measures)是一种有效的测试数据正态性的方法,它提供了更直观的方式来比较观察数据分布与参考分布之间的差异。
下面是一些常见的距离测量方法及其在测试正态性时的应用:
(1) "巴氏距离(Bhattacharyya distance)"的定义是:
- 测量两个分布之间的重叠,通常被解释为两个分布之间的接近程度。
- 选择与观察到的分布具有最小Bhattacharyya距离的参考分布,作为最接近的分布。
(2) 「海林格距离(Hellinger distance)」:
- 用于衡量两个分布之间的相似度,类似于Bhattacharyya距离。
- 与Bhattacharyya距离不同的是,Hellinger距离满足三角不等式,这使得它在一些情况下更为实用。
(3) "KL 散度(KL Divergence)":
- 它本身并不是严格意义上的“距离度量”,但在测试正态性时可以用作衡量信息丢失的指标。
- 选择与观察到的分布具有最小KL散度的参考分布,作为最接近的分布。
运用这些距离测量方法,我们能够比对观测到的分布与多个参考分布之间的差异,进而更好地评估数据的正态性。通过找出与观察到的分布距离最短的参考分布,我们可以更精确地判断数据是否符合正态分布
以上是確定資料分佈常態性的11種基本方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!

