
一、背景介紹
指標與業務息息相關,其價值在於發現問題和發現亮點,以便及時地解決問題和推廣亮點。隨著電商業務的進一步發展,業務迭代快、邏輯複雜,指標的數量越來越多,而且指標之間的差異非常大,變化非常快,如何能夠快速識別系統各項異常指標,發現問題的根因,對業務來說至關重要。如果透過手動的方式去設定警報閾值容易出現疏漏,且非常耗時,成本較高。我們希望建立一套自動化方法,能夠達成以下目標:
- 自動化無需依賴使用者輸入:傳統的方式是需要定義例外規則、歸因維度等等,在自動化系統中不再需要使用者手動輸入。
- 通用性:能夠適應多種多樣的指標分佈,不同的指標會搭配不同的方法。
- 時效性:實現天級、小時的指標異常檢測與歸因。
- 準確度與主動性:達成資料找人的目標。
接下來將分別介紹指標異常檢測、指標異常診斷。
二、指標異常檢測
1、異常有哪些
##資料科學工作的第一步是對問題進行定義。我們對異常的定義是資料指標的異常,指標的過高過低、大起大落都不正常,都需要預警與診斷。指標的異常分為以下三種:

- #絕對值異常
指的是不遵循指標固有的分佈,在統計上的離群點,它反映的是業務當下的狀態。
- 波動異常
#環比過大的突增點或突降點,反映的是業務當下突然的變化。
- 趨勢異常
#前兩種例外是偏單點的,是短暫劇烈的,而有些異常則相對隱蔽,是在中長期呈現出確定性上升或下降的趨勢,往往預示著某些潛在的風險,所以我們也要進行趨勢的異常檢測,進行業務預警和提前乾預。
這三種異常是相互獨立的,不同的場景可能對應不同類型的例外。
例如上圖中A點同時發生了絕對值異常和波動率異常,B點因為與上一天的環比變化不大,所以只報了絕對值異常。 C點和D點都只報了波動異常,但原因是不一樣的,C點指標突降的原因是由B點造成,屬於指標的正常回落,這種需要透過後處理邏輯解決。
2、指標異常將測框架
#為了實現指標檢測的通用性、自動化以及時效性,我們設計了一套基於統計檢定的無監督檢測框架。
- 絕對值異常檢測
#首先絕對值偵測主要是基於GESD 檢定演算法,它的原理是透過計算統計量來尋找異常點。過程如下:
假設資料集中有最多r個異常值。第一步先找到離平均數最大的樣本i,再計算統計量Ri,也就是xi 減去平均數後的絕對值,除以標準差。接下來計算對應的樣本點i的臨界值λi,其中的參數,n 是總共的樣本量,i是已剔除的第幾個樣本,t是具有n-i-1自由度的t 分佈的p 百分點,而p與設定的置信度α(一般α取值為0.05)及目前樣本量有關。
第二步是透過剔除離平均值最大的樣本i,然後重複上面步驟,總共r次。
第三步驟尋找統計量 Ri 大於λi的樣本,即為異常點。
這種方法的優點,一是無需指定異常值的個數,只需要設定異常的上限,在上限範圍內,演算法會自動捕捉異常點;二是克服了3Sigma檢出率過低(小於1%),只能檢出非常極端異常的問題。
在GESD演算法中可以透過控制檢出率的上限去做適應,但這個方法的前提是要求輸入的指標是常態分佈。我們目前觀測的電商業務指標絕大多數是屬於常態分佈的,當然也有個別業務指標(
- 波動異常檢測
第二種是波動異常檢測,主要是基於波動率分佈,計算分佈的拐點。這裡不能直接對波動率分佈套用上面的辦法,主要是因為指標波動率絕大多數不是常態分佈所以不適用。找拐點的原理是基於二階導數和距離來找出曲線上的最大彎曲點。成長的波動率大於0,下降的波動率小於0,針對在y 軸兩側大於0 和小於0 的部分,分別要找兩個波動率的拐點,波動率超出拐點的範圍,就認為是波動異常。但個別情況下拐點會不存在,或是拐點來得太早,導致檢出率太高,所以也需要其他的方法來兜底,如quantile。一種檢驗方法不是萬能的,需要組合來使用。
- 趨勢異常檢測
第三種是趨勢異常檢測,基於Man-Kendall檢定。先計算統計量S, 其中sgn 是符號函數,根據指標序列前後值的相對大小關係,兩兩配對可以得到 -1、1、0 這樣3個映射值。將統計量S做標準化,就得到了Z,可以用查表的方式換算到p值。統計學上當 p 值小於 0.05,就認為有顯著性的趨勢。
它的優點一是非參數檢驗,即可以適用於所有的分佈,因此不需要兜底方法。優點二是不要求指標序列連續,因為在進行趨勢異常檢測的時候,需要事先剔除絕對值異常的樣本,所以大多數指標序列並不連續,但這個方法是可以支持指標不連續的。
- 異常檢測後處理
三種異常結束之後,需要進行後處理的工作,目的主要是減少不必要的警報,降低對業務的干擾。
第一種是資料異常,這的資料異常不是指資料來源出錯了,因為資料來源是在數倉層面,由數倉團隊來保證。這裡的數據異常指的是上週期的異常導致了本週期的波動異常,例如某個指標昨天上漲了100%,今天又下降了50%,這種情況就需要基於規則來進行剔除,剔除的條件就是(1)上個週期存在波動或絕對值異常(2)本週期的波動屬於迴歸正常的,即有波動異常但無和波動異常同向的絕對值異常。例如昨天上漲了100%,今天下降 50% ,經後處理模組會過濾掉,但是如果下降了99%,此時觸發了絕對值異常還是需要預警的。透過這種方式我們一共剔除了40% 以上的波動異常。
第二種後處理是基於S級大促的資訊協同,這種大促中每個小時都可能會出現指標的異常,大家都知道原因,因此沒有必要去進行播報。
三、指標異常診斷
1、指標異常診斷層次分割
根據結論的可行域與確定性,可以將推論分為三個層次,即確定性推論、可能性推論和猜測性推論。

2、指標異常診斷方法比較
不同推論層次對應不同的診斷方法。

猜測性推斷,結論主要依賴人的經驗,結論相對不明確,可操作空間有限,不在本文的方法討論範圍之內。
可能性推斷,(1)可以基於機器學習去擬合指標數據,做迴歸預測,計算特徵的重要性,這種方法的缺點是不能解釋單次異常的原因。 (2)如果想解釋單次的異常要加上一個 shap value 演算法,它可以計算每一次預測值,每一個輸入特徵對於目標的貢獻值。這種方法具有一定的可解釋性,但是不夠精準,而且只能得出相關性,並非因果性。 (3)可以透過貝葉斯網絡來建構指標間關係的圖和網絡,但缺點是計算相對複雜,並且黑盒。
確定性推斷,主要是基於拆解貢獻度演算法。拆解貢獻度演算法不管是加法、乘法或除法,都是以拆解方式來衡量各部分指標或結構的變化對整體的影響。優點是確定性比較強,白盒化,適應性比較強,能夠精準定位到異常所在的位置。但它也存在其天然的缺點,就是針對同一個指標,有非常多的維度可以去拆解,會帶來組合維度爆炸的問題。
3、業務現況
資料科學的許多問題都需要結合業務的實際場景來選擇相應的方法。因此在介紹我們的方法之前,先來介紹一下業務現況。

我們知道,平台電商的成長方式是由流量留存和付費轉換所驅動的。隨著人口紅利見頂,流量獲取日益困難,網易嚴選進行了戰略升級,由平台電商轉型成為品牌電商,將京東、淘寶等平台電商轉變成品牌合作夥伴。
而品牌電商的成長驅動方式是透過全通路協同爆品突圍,塑造明星品類來立住品牌。例如大家了解網易嚴選不一定是透過我們的APP,可能是透過淘寶、京東上買了一些商品來了解我們這個品牌。網易嚴選的成長視角從圍繞用戶的拉新、留存、付費,轉化為了圍繞爆品商品的打造和管道的突破增長。
品牌電商的指標分級可分為戰略層、戰術層、執行層。戰略層對應的是一級指標,即北極星指標。例如大盤的GMV,它衡量的是目標的達成情況,服務公司的策略決策。戰術層對應的是二級指標,是透過將一級指標分拆到各級部門和業務線得到的,服務的是過程管理。執行層對應的是三級指標,是將二級指標進一步拆分到各級類目商品以及負責人,服務具體實施。
基於目前品牌電商的這種指標分級方式,以及需要定位到部門、人、商品這樣的需求,所以需要我們的演算法具有確定性、可解釋性和白盒化。因此我們採用了基於拆解的方式,計算每一層每部分的指標對於整體的影響佔比,也就是前面提到的拆解貢獻度方法。
4、拆解貢獻度計算方法
貢獻度的計算方式包括三種,一類是加法,一類是乘法,還有一類是除法。

拆解方法如上圖所示。 Y是要進行拆解的目標指標,例如大盤的GMV,Xi是其下某個拆分維度下第i 個維值,例如某個省市的GMV,Xi1 代表目前週期的指標,Xi0 表示上一個週期的原始值。
加法的拆解公式很好理解,每個維值的變化值ΔXi除以整體的原始值Y0# ,就是它的貢獻度。
乘法拆解採用了LMDI(Logarithmic Mean Index Method)乘積因子拆解的方式。兩邊同時取對數ln,即可得到加法形式,再依照上述方法,就可以得到各因子的貢獻度。維值的前後比率比較大,貢獻度就比較大。
除法採用雙因素拆解法,即每一個部分、每一個維值對整體的貢獻度是由兩個因素所構成。第一個因素是波動貢獻,以AXi 表示;第二個因素是結構變化貢獻BXi,也就是每個部分的結構變化貢獻。舉個例子,每個部門的毛利率都提升了但整個公司的毛利率卻下降了。原因大機率就是某個低毛利的部門銷售佔比變大了,拖垮了整體,也就是我們熟知的辛普森悖論的情況。除法拆解演算法中,引進BXi這部分結構變化的貢獻,就能夠解決這個問題。
貢獻度的一個很重要的特性就是可加性,滿足 MECE 不重不漏的原則。不管哪一種拆解方式,把某個拆解維度下的全部維值貢獻 CXi加和,都可以得到整體的變化率ΔY%。
5、指標拆解維度爆炸問題

#假設我們對某個一級指標的異常原因進行拆解,例如銷售額或毛利額等等,分割的維度可以是銷售通路或省市地區,也可以依照商品的品類、新舊客等。假設有 n 種拆分維度,那麼就需要產生 n 個維度對應的中間表,然後針對每個維度下面的每一個維度值Xi,去計算指標變化,才能得到其貢獻度。
為了精準地找到指標異常的原因,面臨的問題是只拆單一維度,只能得到該維度的結論,定位不到精準的問題所在。如果拆解的維度太細,例如把所有的維度都組合,那每一項的貢獻度又太小,還是無法得到主要的原因。所以這裡需要層層的下鑽和窮舉,在各種維度組合中搜尋我們想要的結論。
假設目前有n 種分割維度,那麼就需要先建立2n個中間表,建立中間表的過程中要確保口徑一致,並滿足數倉規範,工作量是非常大的。建好這些中間表之後,再分別呼叫拆解演算法的API計算對應的貢獻度,這就產生了非常大的運算和儲存消耗,也就是維度爆炸的問題。
6、指標拆解維度爆炸問題最佳化

#為了解決維度爆炸的問題,對實作方案進行了以下最佳化:
優化1:把維度拆解的流程轉換成基於貢獻度聚合。前文提到,因為貢獻度具有可加性,首先調用一次演算法計算最細粒度的末級指標的貢獻度,然後需要哪個維度的貢獻度,就用它去做group by 條件對貢獻度求和。這樣能夠省略中間表的 IO 過程,只需要一次演算法調用,在叢集上執行求和操作也會比調用指標拆解演算法快得多。
上述是針對一級指標進行的異常診斷,我們實際業務中還需要對二級指標進行診斷,這種方法只需要再對貢獻度做一次歸一化即可,不需要重複計算,可以針對一級、二級指標同時進行異常診斷。
計算效率的問題得以解決,但仍存在一個問題,即結果的空間複雜度非常大,達 。假設k是平均每個維度下的維值個數,單一維度拆解空間
。假設k是平均每個維度下的維值個數,單一維度拆解空間 雙維度拆解空間
雙維度拆解空間 三維度拆解空間
三維度拆解空間  n維度拆解空間
n維度拆解空間 =
= 。
。

優化2:根據實際業務需求限制維度組合實作剪枝,將結果的空間複雜度從 降至
降至
 #圖片
#圖片
以內。具體包含兩個操作,第一個是將維度分組,對於具有天然層次關係的維度,例如一級渠道和二級渠道,如果拆到二級渠道,其實一級渠道資訊已經有了,就不用對一級渠道和二級渠道進行冗餘的組合了,只需要對於跨組的維度進行組合就可以了。第二個是限制維度組合的維數,因為在歸因診斷分析的時候,實際業務不會關注到特別複雜的維度上去,一般由兩三個維度組合起來就夠用了。
最佳化3:基於維度基尼係數排序,決定最佳維度,實現異常精確定位。有了剪枝後的若干拆分度以及對應的維值貢獻度,如何才能優中選優,定位到主要原因呢?直覺的想法就是某個維度的粒度越細,且頭部top維值貢獻度越大,就越可能是指標異常的最主要原因。基尼係數是比較適合這個場景的度量方式,用1減每一部分的貢獻度的平方和越小,表示拆分維度越合理。
上圖右邊舉了1個例子,針對某次銷售異常,第一種依商品維度去拆,因為每個商品的貢獻度太小,所以基尼係數非常大。第二種依照二級渠道的粒度去拆,粒度比較粗,算出來的基尼係數可能是比較大的值。第三種依照一級產業叉乘二級渠道去算,基尼係數很有可能更小,因為二級渠道再下鑽一層,有的部分出現了正的貢獻度,有的部分出現了負的貢獻度。正的貢獻度就是對於指標的波動有正向正向效果的部分,負向貢獻度就是有負向作用的。在這個例子中可以看到拆分維度產業1叉乘管道1貢獻度60%,被歸為主因,也是比較符合我們認知的。所以透過基尼係數我們能夠找到較合理的拆分維度和導致指標異常的主要原因。
四、QA
Q1: 請問用什麼指標評估診斷的準確率?
A1: 因為我們用的是確定性診斷,所以結論是非常明確的。如果從單純指標這個層面來看,是透過計算寫程式碼實現來保證準確率的。如果從業務理解的角度,例如這次異常是因為某個業務進行了某個正常的操作,或者因為其他原因導致誤報或漏報,這種情況是透過收集badcase的方式來進行準確率的評估。
Q2: 貢獻度的拆解會混合使用嗎?例如GMV的拆解,最初使用加法進行渠道拆解,後續使用乘法公式,如何評判使用不同拆解方式的順序?
A2: 這是一個非常好的實踐上的問題。首先,加法和乘法混合使用這個思路是可行的,可以採用貪心地方式去搜索,算出來每一步的TOP維度值對應貢獻度及下一步拆解後的貢獻度,結合貢獻度下降的多少來確定下一步是透過加法的拆解,還是透過乘法來拆解。
另外一種想法是先按照某一個方向,例如針對電商GMV,可以先透過加法來進行拆解,不斷地拆解,拆解到最底層,例如某個商品,再對這個商品進行乘法拆解,這個商品為什麼GMV 下跌了,是流量下跌了還是轉換率下跌了等等。具體的做法需要結合實際中不同的業務需求,以及時效性、開發成本等方面的考量。
在網易嚴選目前的場景中,考慮到通用性以及業務現狀,作為品牌電商,在外渠售賣的時候,流量、轉換率等因素對於我們來講是黑盒子的,所以在我們的業務場景中,主要是以加法拆解為主。
以上是網易如何做到資料指標異常發現與診斷分析?的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 AI內部部署的隱藏危險:治理差距和災難性風險Apr 28, 2025 am 11:12 AM
AI內部部署的隱藏危險:治理差距和災難性風險Apr 28, 2025 am 11:12 AMApollo Research的一份新報告顯示,先進的AI系統的不受檢查的內部部署構成了重大風險。 在大型人工智能公司中缺乏監督,普遍存在,允許潛在的災難性結果
 構建AI測謊儀Apr 28, 2025 am 11:11 AM
構建AI測謊儀Apr 28, 2025 am 11:11 AM傳統測謊儀已經過時了。依靠腕帶連接的指針,打印出受試者生命體徵和身體反應的測謊儀,在識破謊言方面並不精確。這就是為什麼測謊結果通常不被法庭採納的原因,儘管它曾導致許多無辜者入獄。 相比之下,人工智能是一個強大的數據引擎,其工作原理是全方位觀察。這意味著科學家可以通過多種途徑將人工智能應用於尋求真相的應用中。 一種方法是像測謊儀一樣分析被審問者的生命體徵反應,但採用更詳細、更精確的比較分析。 另一種方法是利用語言標記來分析人們實際所說的話,並運用邏輯和推理。 俗話說,一個謊言會滋生另一個謊言,最終
 AI是否已清除航空航天行業的起飛?Apr 28, 2025 am 11:10 AM
AI是否已清除航空航天行業的起飛?Apr 28, 2025 am 11:10 AM航空航天業是創新的先驅,它利用AI應對其最複雜的挑戰。 現代航空的越來越複雜性需要AI的自動化和實時智能功能,以提高安全性,降低操作
 觀看北京的春季機器人比賽Apr 28, 2025 am 11:09 AM
觀看北京的春季機器人比賽Apr 28, 2025 am 11:09 AM機器人技術的飛速發展為我們帶來了一個引人入勝的案例研究。 來自Noetix的N2機器人重達40多磅,身高3英尺,據說可以後空翻。 Unitree公司推出的G1機器人重量約為N2的兩倍,身高約4英尺。比賽中還有許多體型更小的類人機器人參賽,甚至還有一款由風扇驅動前進的機器人。 數據解讀 這場半程馬拉松吸引了超過12,000名觀眾,但只有21台類人機器人參賽。儘管政府指出參賽機器人賽前進行了“強化訓練”,但並非所有機器人均完成了全程比賽。 冠軍——由北京類人機器人創新中心研發的Tiangong Ult
 鏡子陷阱:人工智能倫理和人類想像力的崩潰Apr 28, 2025 am 11:08 AM
鏡子陷阱:人工智能倫理和人類想像力的崩潰Apr 28, 2025 am 11:08 AM人工智能以目前的形式並不是真正智能的。它擅長模仿和完善現有數據。 我們不是在創造人工智能,而是人工推斷 - 處理信息的機器,而人類則
 新的Google洩漏揭示了方便的Google照片功能更新Apr 28, 2025 am 11:07 AM
新的Google洩漏揭示了方便的Google照片功能更新Apr 28, 2025 am 11:07 AM一份報告發現,在谷歌相冊Android版7.26版本的代碼中隱藏了一個更新的界面,每次查看照片時,都會在屏幕底部顯示一行新檢測到的面孔縮略圖。 新的面部縮略圖缺少姓名標籤,所以我懷疑您需要單獨點擊它們才能查看有關每個檢測到的人員的更多信息。就目前而言,此功能除了谷歌相冊已在您的圖像中找到這些人之外,不提供任何其他信息。 此功能尚未上線,因此我們不知道谷歌將如何準確地使用它。谷歌可以使用縮略圖來加快查找所選人員的更多照片的速度,或者可能用於其他目的,例如選擇要編輯的個人。我們拭目以待。 就目前而言
 加固芬特的指南 - 分析VidhyaApr 28, 2025 am 09:30 AM
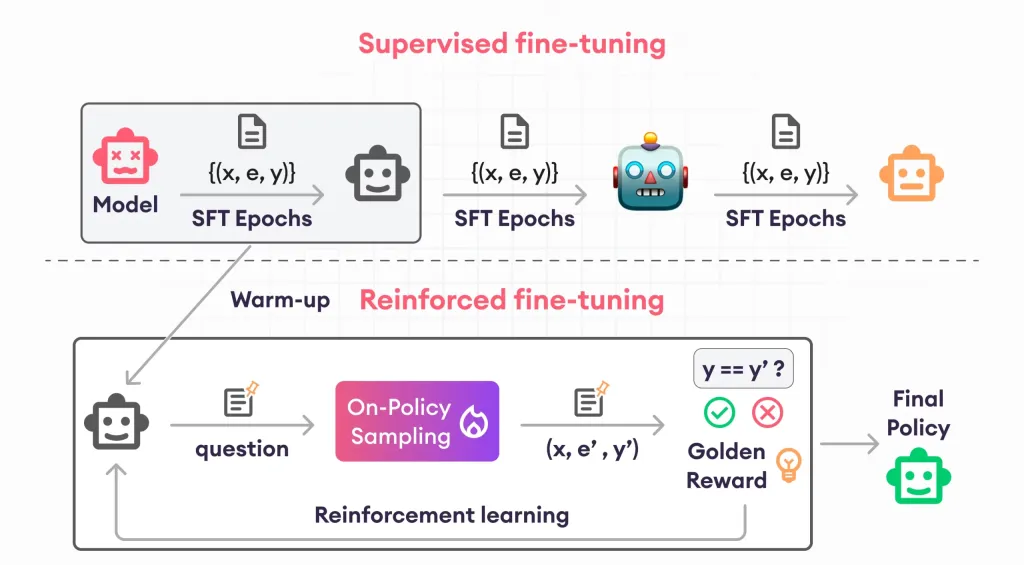
加固芬特的指南 - 分析VidhyaApr 28, 2025 am 09:30 AM增強者通過教授模型根據人類反饋進行調整來震撼AI的開發。它將監督的學習基金會與基於獎勵的更新融合在一起,使其更安全,更準確,真正地幫助
 讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM
讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM科學家已經廣泛研究了人類和更簡單的神經網絡(如秀麗隱桿線蟲中的神經網絡),以了解其功能。 但是,出現了一個關鍵問題:我們如何使自己的神經網絡與新穎的AI一起有效地工作


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

SublimeText3漢化版
中文版,非常好用

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

Dreamweaver CS6
視覺化網頁開發工具

WebStorm Mac版
好用的JavaScript開發工具

Safe Exam Browser
Safe Exam Browser是一個安全的瀏覽器環境,安全地進行線上考試。該軟體將任何電腦變成一個安全的工作站。它控制對任何實用工具的訪問,並防止學生使用未經授權的資源。






