陶哲軒瘋狂安麗Copilot：它幫我完成了一頁紙證明，甚至能猜出我後面的過程

繼給GPT-4「代言」之後，Copilot也被陶哲軒瘋狂安麗。

他直言，在程式設計時，Copilot能直接預測他下一步要做什麼。

有了Copilot之後，研究做起來也更方便了，陶哲軒也用它輔助自己完成了最新的研究成果。

陶哲軒說，這次的論文中，有關這部分的內容其實只有一頁。

但具體完成這一頁紙的證明，他足足寫了200多行程式碼，用的還是新學的程式語言Lean4。

而在陶哲軒公開程式碼的GitHub頁面上顯示，Copilot將寫程式碼的速度提升了一半以上。

陶哲軒介紹，之所以選擇Lean4是看中了它的“重寫策略”，也就是對一長段表達式進行針對性的局部替換。

舉個例子，假如定義了一個複雜的函數f(x)，當我們想要輸入f(114514)的表達式時，直接用程式碼把x「重寫」成114514就可以了。

陶哲軒說，這個特性比起需要重複輸入公式的LaTeX簡直不要太方便。

那麼陶哲軒這次的「一頁紙證明」又為我們帶來了什麼新成果呢？

一頁紙證明新不等式

這篇論文談論了有關麥克勞林不等式的問題。

麥克勞林不等式是數學中一個經典的不等式，它基於「非負實數的算數平均值大於等於幾何平均值」這一定律導出，可以表述為：

設y₁…y_n為非負實數，對k=1…n，定義平均值S_k為（分母為分子的項數）：

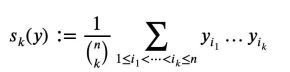
它是作為具有根的n 次多項式的歸一化係數而出現。

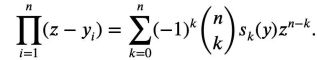
（記得這個式子，我們稱它為式1）

則麥克勞林不等式可以表示為：

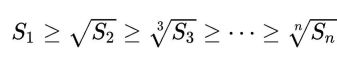
#其中，當且僅當所有y_i相等時等號成立。

在微積分中，還有一個經典的牛頓不等式：

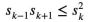
對任意1≤kn都是非負，牛頓不等式就可以簡單地描述麥克勞林不等式了：

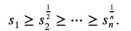
#但如果不加上這個限制條件，即允許負數項的存在，用牛頓不等式就無法表示麥克勞林不等式了。

於是針對牛頓不等式中可能存在負數項的情況，陶哲軒提出了一組新的不等式變體：

對任意r>0且1≤ℓ≤n，必有式2或式3成立。

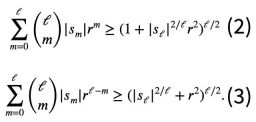
這便是陶哲軒這一頁紙所要證明的內容，具體證明過程是這樣的：

不妨建構一個關於複雜變數z的多項式P(z)：

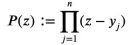
由前面的式1和三角不等式可得：

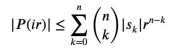
所以只需要建立下界：

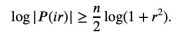
對P(z)取絕對值再取對數可得：

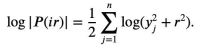
由於對任意實數t，t ↦ log(e^t a)呈凸性且a>0，可以得到不等式：

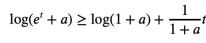
當a=r²，t=2log y_j時，可以得到：

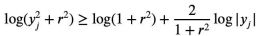
以上就是陶哲軒給出的證明過程，但是，當歸一化的|S_n|=1時，下式成立：

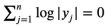
下一步：建立細化版本

除了這次提到的“一頁紙證明”，陶哲軒的這篇論文中還提出了另一項新的定理，即對任意1 ≤ k ≤ ℓ≤ n.：

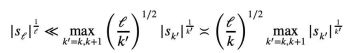
在部落格文章中，陶哲軒透露，他的下一步計畫就是提出這一不等式的細化版本。

陶哲軒說，證明的過程「就像練習一樣」會很簡單，用微積分就能搞定。

不過，他也提到會有一個小困難，因為這部分論證過程使用到了漸進符號。

新的結論具體怎樣，讓我們拭目以待。

One More Thing

陶哲軒可謂是AI工具的忠實粉絲，Copilot、GPT-4，還有一些其他輔助工具都受到他的推薦。

這次，他也對大模型的發展提出了新的期待，希望有一天模型可以直接產生不等式變體。

論文網址：https://arxiv.org/abs/2310.05328 

#

以上是陶哲軒瘋狂安麗Copilot：它幫我完成了一頁紙證明，甚至能猜出我後面的過程的詳細內容。更多資訊請關注PHP中文網其他相關文章！