利用高斯混合模型對多模態分佈進行分解

使用高斯混合模型可以將一維多模態分佈拆分為多個分佈

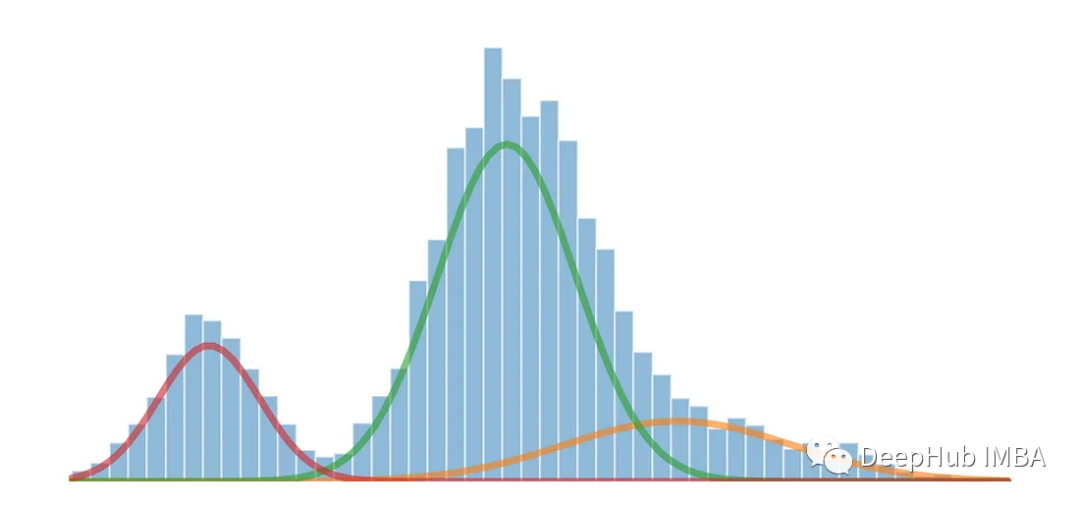
#高斯混合模型（Gaussian Mixture  Models，簡稱GMM）是一種在統計和機器學習領域中常用的機率模型，用於對複雜資料分佈進行建模和分析。 GMM  是一種生成模型，它假設觀測資料是由多個高斯分佈組合而成的，每個高斯分佈稱為一個分量，這些分量透過權重來控制其在資料中的貢獻。

產生具有多模態分佈的資料

#當一個資料集顯示出多個不同的峰值或模態時，通常意味著資料集中存在多個突出的資料點簇或集中。每個模態代表了分佈中一個突出的資料點簇或集中，可以被視為資料值更可能出現的高密度區域

我們將使用numpy產生的一維數組。

import numpy as np  dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500)  multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)

讓我們把一維的資料分佈形象化。

import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid')  plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()

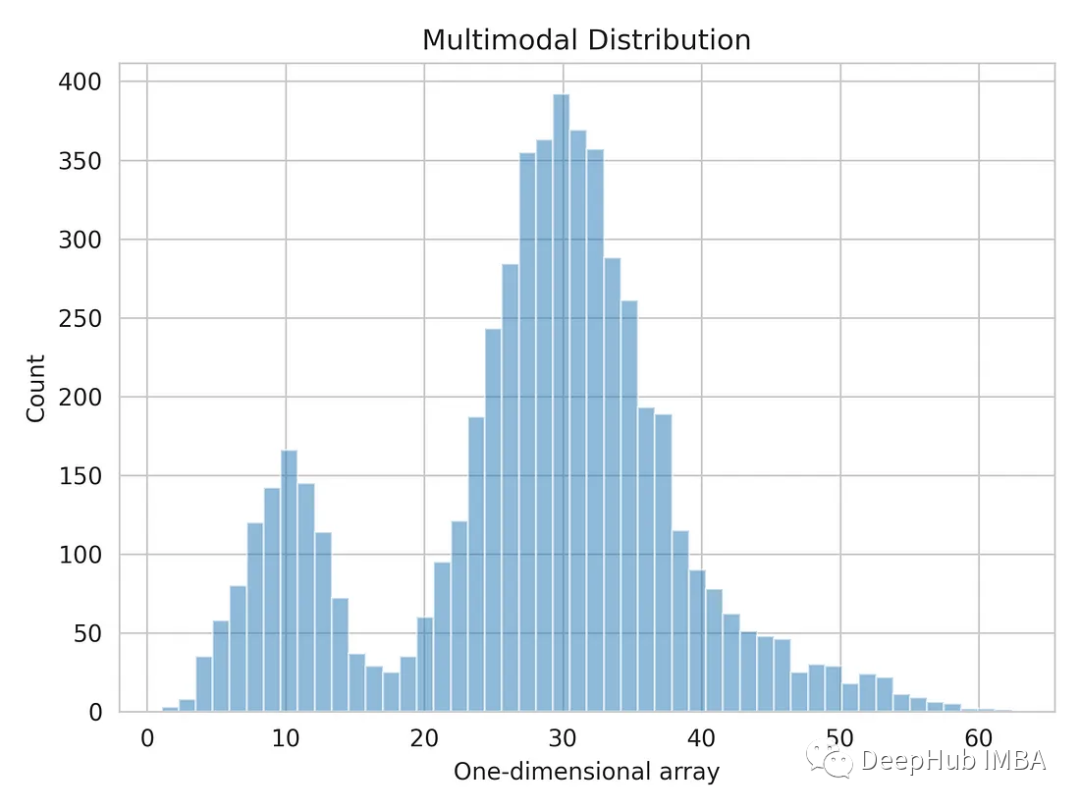
使用高斯混合模型拆分多模態分佈

我們將使用高斯混合模型來計算每個分佈的平均值和標準差，將多模態分佈分離為三個原始分佈。高斯混合模型是一種無監督機率模型，可用於資料聚類。它使用期望最大化演算法來估計密度區域

from sklearn.mixture import GaussianMixture  gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1))  means = gmm.means_  # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5  # Useful when plotting the distributions later weights = gmm.weights_   print(f"Means: {means}, Standard Deviations: {standard_deviations}")  #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]

我們已經得到了平均值和標準差，可以對原始分佈進行建模。可以看到雖然平均值和標準差可能不完全正確，但它們提供了一個接近的估計值。

把我們的估計和原始資料比較一下。

from scipy.stats import norm  fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))  for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):axes[0].hist(dist, bins=bins, alpha=0.5)  axes[1].hist(multimodal_dist, bins=50, alpha=0.5)  x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)  for mean, covariance, weight in zip(means, standard_deviations, weights):pdf = weight*norm.pdf(x, mean, std)plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)  plt.show()

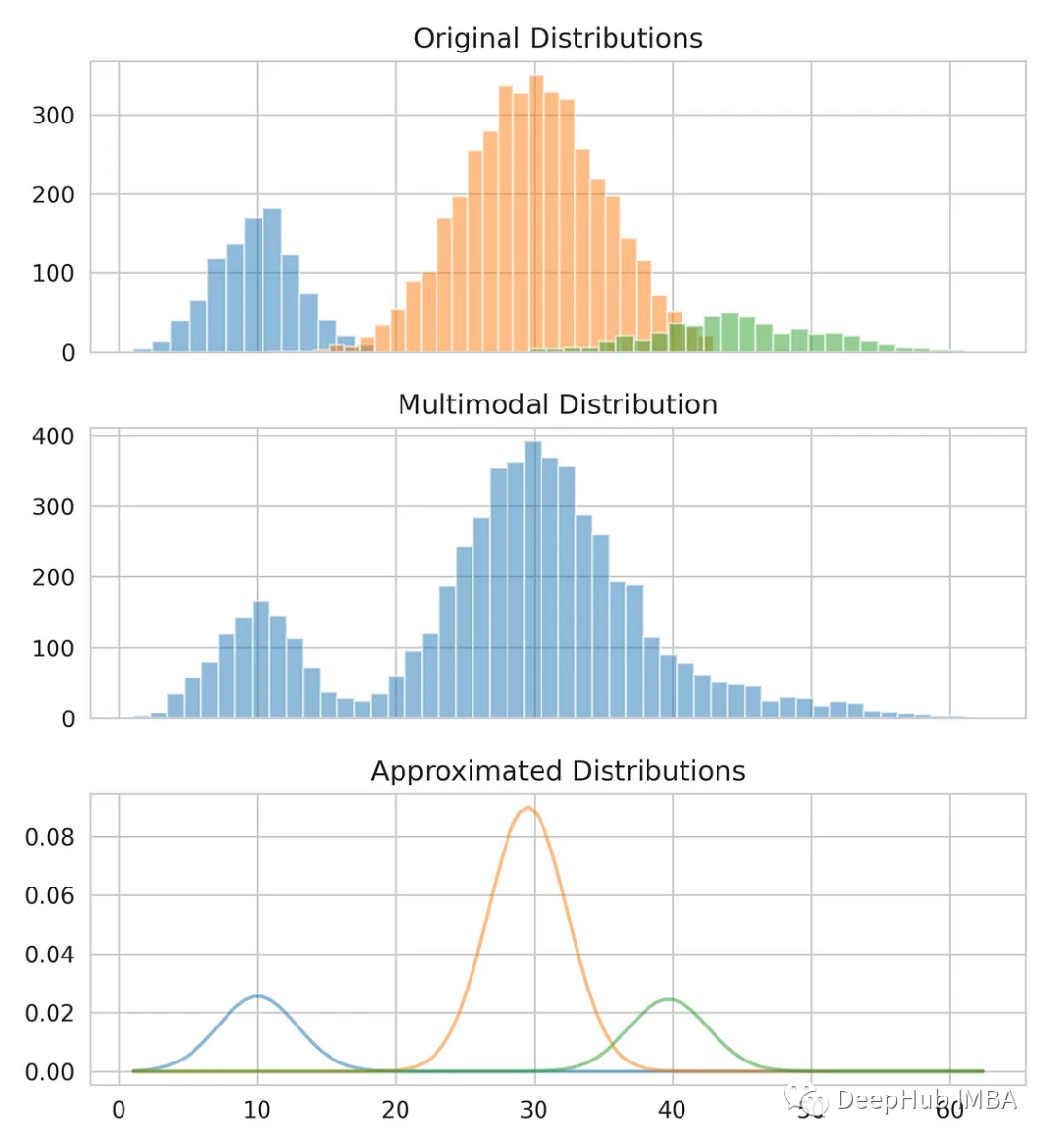
#總結

#高斯混合模型是一個功能強大的工具，可以用來對複雜的數據分佈進行建模和分析，同時也是許多機器學習演算法的基礎之一。它的應用範圍廣泛，可以解決各種資料建模和分析問題

這個方法可以用作一種特徵工程技術，來估計輸入變數內子分佈的置信區間

以上是利用高斯混合模型對多模態分佈進行分解的詳細內容。更多資訊請關注PHP中文網其他相關文章！