使用歸併排序演算法編寫的C/C++程式來計算數組中的逆序對數？

對給定數組進行排序時發生的反轉計數稱為反轉計數。逆問題是一個經典問題，可以使用歸併排序演算法來解決。在此問題 v 中，我們將計算其左側大於它的所有元素，並將計數新增至輸出。這個邏輯是在合併排序的合併函數中完成的。

為了更好地理解這個主題，讓我們舉個例子。讓我們考慮合併過程中涉及的兩個子陣列-

## 

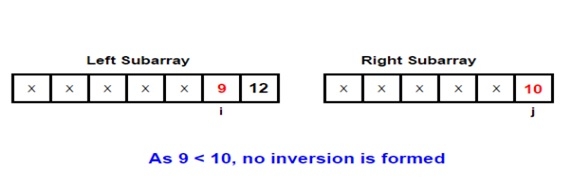
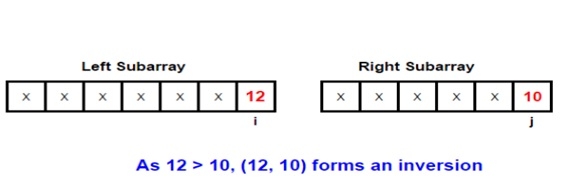Input: arr[] = { 1, 9, 6, 4, 5}
Output: Inversion count is 5

說明

陣列的反轉次數

給定一個陣列，找出它的反轉次數。如果 (i A[j]) 則 (i, j) 對稱為陣列 A 的反轉。我們需要對arr 中所有此類對進行計數

例如，

數組中有5個反轉

(9,6), (9,4), (9,5), (6,4), (6,5)

#1.互相比較元素的值。

2.如果較低索引處的值較高，則增加計數器。

3.顯示結果。

範例

#include <stdio.h>
int Merge(int arr[], int aux[], int low, int mid, int high) {
   int k = low, i = low, j = mid + 1;
   int inversionCount = 0;
   while (i <= mid && j <= high) {
      if (arr[i] <= arr[j]) {
         aux[k++] = arr[i++];
      } else {
         aux[k++] = arr[j++];
         inversionCount += (mid - i + 1); // NOTE
      }
   }
   while (i <= mid)
   aux[k++] = arr[i++];
   for (int i = low; i <= high; i++)
      arr[i] = aux[i];
   return inversionCount;
}
int MergeSort(int arr[], int aux[], int low, int high) {
   if (high == low) // if run size == 1
      return 0;
   int mid = (low + ((high - low) >> 1));
   int inversionCount = 0;
   inversionCount += MergeSort(arr, aux, low, mid);
   inversionCount += MergeSort(arr, aux, mid + 1, high);
   inversionCount += Merge(arr, aux, low, mid, high);
   return inversionCount;
}
int main() {
   int arr[] = { 1, 9, 6, 4, 5 };
   int N = 5;
   int aux[N];
   for (int i = 0; i < N; i++)
      aux[i] = arr[i];
   printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1));
   return 0;
}

#

以上是使用歸併排序演算法編寫的C/C++程式來計算數組中的逆序對數？的詳細內容。更多資訊請關注PHP中文網其他相關文章！