JavaScript演算法之歸併排序演算法（詳解）

在本文中，我們學習 Merge Sort 背後的邏輯，並用 JavaScript 實作。最後，在空間和時間複雜度方面將歸併排序與其他演算法進行比較。

歸併排序背後的邏輯

歸併排序使用分而治之的概念對給定的元素列表進行排序。它將問題分解為較小的子問題，直到它們變得足夠簡單以至可以直接解決為止。

以下是歸併排序的步驟：

1、將給定的列表分為兩半（如果列表中的元素數為奇數，則使其大致相等）。

2、以相同的方式繼續分割子數組，直到只剩下單一元素數組。

3、從單一元素數組開始，合併子數組，以便對每個合併的子數組進行排序。

4、重複第 3 步單元，直到最後得到一個排好序的陣列。

以陣列[4, 8, 7, 2, 11, 1, 3] 為例，讓我們來看看歸併排序是如何運作的：

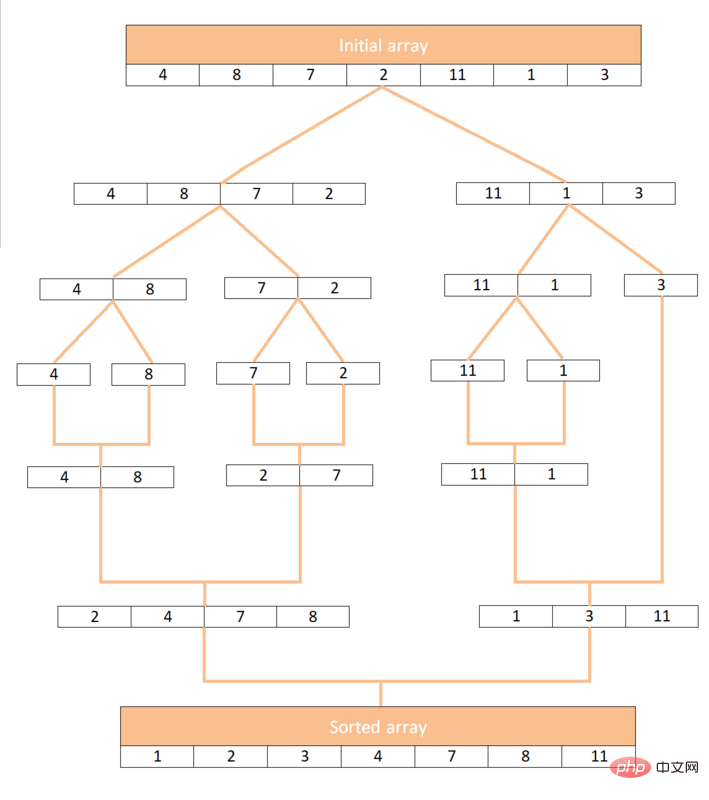
#用JavaScript 實作歸併排序

首先實作一個將兩個已排序子數組合併為一個已排序數組的函數merge() 。要注意著兩個子數組是已經被排好序的，這一點非常重要， merge() 函數只用於其進行合併。 【推薦教學：《JavaScript影片教學》】

可以透過遍歷這兩個子數組來實現：

function merge(left, right) {
    let arr = []
    // 如果任何一个数组为空，就退出循环
    while (left.length && right.length) {
        // 从左右子数组的最小元素中选择较小的元素
        if (left[0] < right[0]) {
            arr.push(left.shift())  
        } else {
            arr.push(right.shift()) 
        }
    }
    
    // 连接剩余的元素，防止没有把两个数组遍历完整
    return [ ...arr, ...left, ...right ]
}

在這個函數中，透過把兩個排好序的子數組（left、right）合併來獲得一個排好序的大數組。首先，建立一個空數組。之後在 left 和 right 兩個子數組中最小元素中的較小的一個，並將其添加到空數組。我們只需要檢查 left 和 right 子數組中的第一個元素，因為它們是已排好序的。

在這個過程中，從子陣列中刪除了被選取的元素（透過 shift()  函數實作）。繼續這個過程，直到其中一個子數組變成空。最後把非空子數組的剩餘元素（因為它們已經被排序）插入主數組的最後面。

現在有了合併兩個已排序數組的程式碼，接下來為實現歸併排序演算法的最終程式碼。這表示要繼續分割數組，直到最終只包含一個元素的數組為止：

function mergeSort(array) {
  const half = array.length / 2
  
  if(array.length < 2){
    return array 
  }
  
  const left = array.splice(0, half)
  return merge(mergeSort(left),mergeSort(array))
}

在程式碼中先確定中點，並用splice() 函數將陣列分成兩個子數組。如果元素數量為奇數，則左側的元素數量會少一個。不斷的劃分數組，直到剩下單一元素的數組（array.length ）。然後用之前實作的 <code>merge() 函數合併子數組。

程式碼實作後用前面的用例測試一下：

array = [4, 8, 7, 2, 11, 1, 3];
console.log(mergeSort(array));

輸出符合預期：

1,2,3,4,7,8,11

歸併排序的效率

歸併排序的最差時間複雜度為$O(n\\log n)$，與快速排序的最佳情時間複雜度相同。歸併排序是目前最快的排序演算法之一。

與快速排序不同，歸併排序不是in-place排序演算法，這表示除了輸入陣列之外，它還會佔用額外的空間。這是因為我們使用了輔助數組來儲存子數組。歸併排序的空間複雜度為  $O(n)$。

歸併排序的另一個優點是非常適合多線程，因為每個被分割的一半都可以單獨排序。另一種常見的減少歸併排序運行時間的方法是在到達相對較小的子數組時（大約 7 個元素）使用插入排序。這是因為插入排序在處理小型或幾乎排好序的陣列時表現非常好。

總結

在本文中，我們了解了Merge Sort演算法背後的邏輯，並且用 JavaScript 實作。它是基本排序演算法之一，可以幫助我們更好的了解分治法策略。

更多程式相關知識，請造訪：程式設計影片課程！ ！

以上是JavaScript演算法之歸併排序演算法（詳解）的詳細內容。更多資訊請關注PHP中文網其他相關文章！