GPT-4透過97輪對話探索全球難題，得出P≠NP的​​結論

對於身處科研領域的人來說，或多或少的都聽過P/NP 問題，該問題被克雷數學研究所收錄在千禧年大獎難題中，裡面有七大難題，大家熟知的龐加萊猜想、黎曼假設等都包含在內。而這個組織也為能夠攻克這個問題的研究人員提供了數百萬美元的獎金懸賞。

P/NP 問題最早在 1971 年由史提芬·庫克（Stephen A. Cook）和列昂尼德·列文分別提出。多年來，許多人都投入研究這個問題。然而，有人表示解決P=NP 問題可能需要保守估計還需要100 年的時間

近年來，有些人聲稱已經證明了P 等於或不等於NP，但這些證明過程都存在錯誤。然而，到目前為止，還沒有人能夠給出一個確切的答案

隨著人工智慧技術的發展，尤其是最近一年大型語言模型的快速更新，研究人員開始嘗試利用人工智慧技術來解決一些全球性難題

研究者來自微軟研究院、北京大學、北航等機構，他們提出使用大語言模型（LLM）來增強和加速對P versus NP問題的研究

本文提出了一個通用框架，即蘇格拉底推理（Socratic reasoning），用於促使LLM進行深入思考並解決複雜問題。在這個框架的基礎上，LLM能夠遞歸地發現、解決和整合問題，同時也能進行自我評估和完善

本文對P vs. NP 問題的試點研究表明， GPT-4 成功地產生了一個證明模式，並在97 輪對話回合中進行了嚴格的推理，得出「P≠ NP」的結論，這與（Xu 和Zhou，2023）結論一致。

請點擊以下連結查看論文：https://arxiv.org/pdf/2309.05689.pdf

#本文的主要貢獻可以總結為：

• 將LLM 作為與人類一起協作的伙伴來應對複雜的科學挑戰，並提出“LLM for Science（LLM4Science ）”範式。
• 引入一個名為「蘇格拉底推理」的框架，鼓勵 LLM 使用演繹、轉換、分解等模式來激發批判性思考。
• 使用 GPT-4 和蘇格拉底推理框架進行試驗研究，以解決理論計算機科學中的 P 與 NP 問題。
• GPT-4 成功地產生了證明模式，並在97 個對話回合中進行了嚴格的推理，得出了P ≠ NP 的結論，與Xu 和Zhou (2023 ) 最近的工作一致。
• 該研究展示了 GPT-4 等 LLM 推斷新知識並與人類合作探索複雜專家級問題的潛在能力。
• 本文強調了 LLM 是跨領域的通用創新領航者，這與先前為特定任務量身定制的專門 AI 模型不同。
• LLM 流暢運用自然和數學語言的能力對於跨學科發現至關重要。
• 這項工作揭示瞭如何利用 LLM 作為合作夥伴來增強和加速跨不同領域的科學研究進程。

重寫後的內容：這段經文中提到，他們將框架命名為「蘇格拉底推理」是受到了古希臘哲學家蘇格拉底的啟發。蘇格拉底曾說過：「我無法教任何人任何東西。我只能讓他們思考。」而這個框架的整體設計思路也是如此，它是一種通用的問題解決框架，允許LLM在廣泛的解決方案空間中導航並有效地得出答案

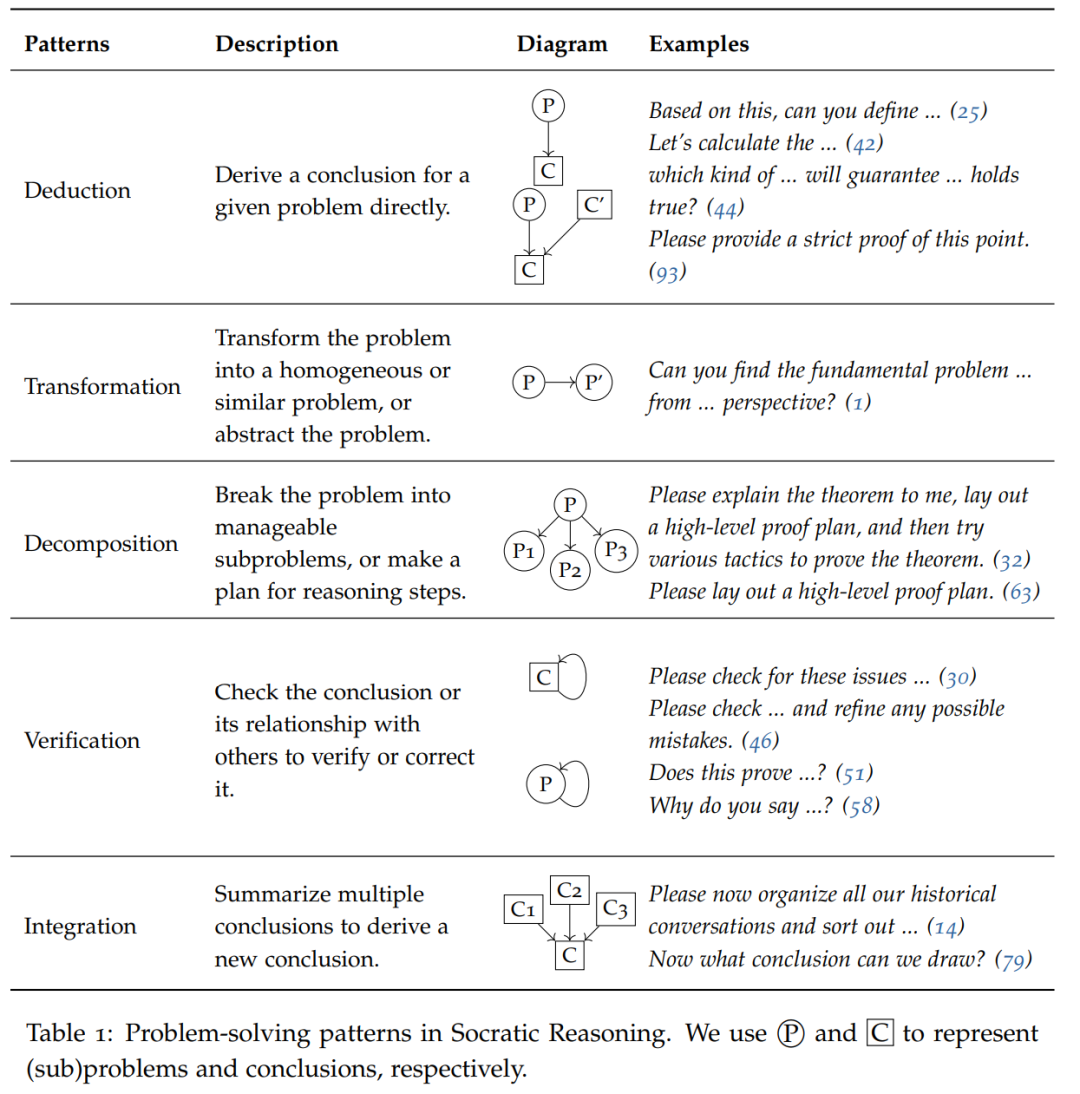
表1中列舉了「蘇格拉底推理」的五種提示模式：演繹、變換、分解、驗證和融合。這些模式被用來發現新的見解和觀點，將複雜的問題分解成子問題或小步驟，並透過挑戰回應答案來進行自我改進

##在較小的問題（ atomic problem）上，LLM 能夠直接給出推理結果，這時採用演繹模式（例如提示語為讓我們一步一步思考…）來指導LLM 直接得出結論。

對於更複雜的問題，本文首先要求 LLM 將問題轉換成一個新問題或將其分解為幾個子問題。然後遞歸地執行這些模式，直到達到原子 ji 問題。

在出現新問題或得出新結論時，應採用驗證模式並利用LLM的自我評估能力進行驗證和改進

最後，融合模式要求LLM根據子問題的結果綜合結論

#透過一系列對話遞歸地激勵LLM 繼續上述過程，直到解決目標問題

在這個工作中，「蘇格拉底推理」為具有挑戰性的問題提供了一個系統的提示框架

#下圖為「蘇格拉底推理」中用來解決P vs. NP 問題的對話範例。案例研究中使用了 GPT-4 API，此外，本文還根據輪次索引對流程進行排序。 

在探索過程中，本文引進了五個不同的角色作為輔助證明者，例如精通機率論的數學家。實驗總共進行了97輪對話，分為前14輪和後83輪對話

#舉個例子，第一輪提示：你能夠從哲學的角度而不是從電腦理論的角度，找出P!=NP背後的根本問題嗎？

以下是其他的提示：

對話不斷進行，最終一輪對話如下：最後得出結論P≠ NP

#有興趣的讀者可以查看原論文，了解更多內容。

以上是GPT-4透過97輪對話探索全球難題，得出P≠NP的​​結論的詳細內容。更多資訊請關注PHP中文網其他相關文章！