如果平面上沒有超過兩個點共線，那麼三角形的數量是多少？

讓我們看看如何在給定 n 個點的平面上計算三角形的數量，並限制共線的點不超過兩個。

計算共線點不超過兩個的平面中的三角形數量是計算幾何中的典型問題，它應用於計算機圖形學、圖像處理和計算機科學的其他領域。

例如，從 3D 圖形中的 3D 場景建立 2D 影像時，可能會出現計算共線點不超過兩個的平面中的三角形的問題。在這種情況下，三角形計數過程可用於確定將 3D 場景投影到平面上後最終 2D 影像中存在多少個三角形。由此可以確定場景的複雜程度，提高渲染速度。

在影像處理中，我們可能想要計算影像中唯一物件或形狀的數量，這個問題很有幫助。在這種情況下，我們可以將圖像表示為平面上的點的集合，然後我們可以透過應用三角形計數技術來計算這些點之間可以創建的三角形的數量。我們可以透過計算形成的三角形數量來確定影像中不同項目或形狀的大致數量。

說明

讓我們透過幾個例子來理解這個問題並嘗試解決它。

目的是確定在具有 n 個點的平面上形成多少個三角形，使得不超過兩個點共線。

範例 -

假設 N 是平面上的點數。

N = 3

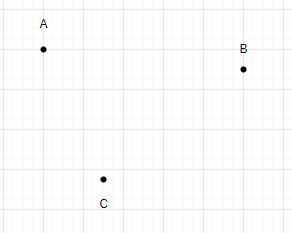
使用這些點我們只能繪製一個三角形。

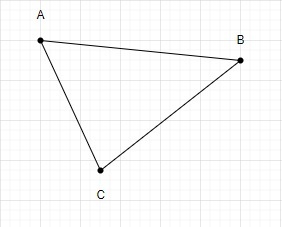
因此，使用 3 個點組成的三角形總數為 1。

讓 N = 4

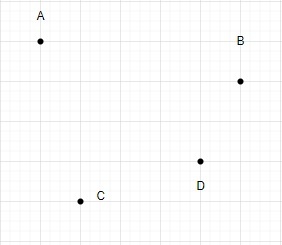
讓我們用這四個點來繪製三角形。

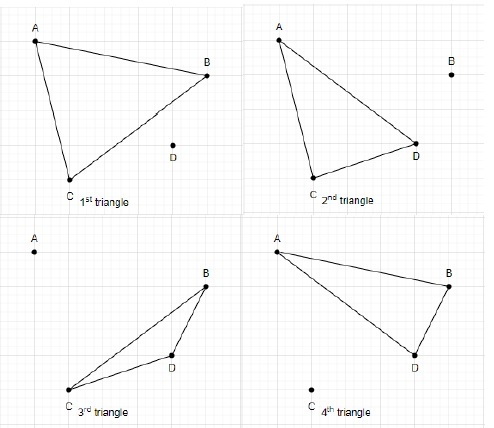
使用 4 個點形成的三角形總數為 4。

讓我們看看計算三角形數量所涉及的一些數學知識。這可以使用排列和組合來獲得。要建立三角形，一次需要總數中的 3 個點。

因此，如果一個平麵包含 n 個點，且其中不超過兩個點共線，則該平面中三角形的數量由以下公式給出。

$$\mathrm{n_{C_{3}}\:=\:\frac{n(n-1)\:(n-2)}{6}}$$

#方法

如果不超過兩個點共線，則程式會尋找平面中三角形的數量，使用下列演算法。

• 將平面上的點數當作輸入，並限制不超過兩個共線點。

• 使用上述公式計算三角形的總數。

• 列印三角形總數作為輸出。

範例

如果不超過兩點共線，則計算平面中三角形的數量的 C 程式。

#include <iostream>
using namespace std;

int main() {
   int number_of_points = 4;
   int number_of_triangle;
   
   number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
   cout << "Total number of triangles formed using " << number_of_points<< " points = " <<  number_of_triangle << endl;
   
   return 0;
}

輸出

Total number of triangles formed using 4 points = 4

複雜性

時間複雜度：O(1)，因為無論輸入大小如何，此程式碼都會執行固定數量的計算。

空間複雜度：O(1)，因為程式碼使用固定數量的變數來儲存輸入值和結果，而不管輸入的大小。

結論

在本文中，我們嘗試解釋尋找具有 n 個給定點的可能三角形總數的方法，約束條件是沒有兩點共線。我希望這篇文章可以幫助您更好地學習這個概念。

以上是如果平面上沒有超過兩個點共線，那麼三角形的數量是多少？的詳細內容。更多資訊請關注PHP中文網其他相關文章！