每天都用！你了解HASH是什麼東東嗎？

HashMap用過吧？ 那麼什麼是Hash你有認真了解過嗎？ 本文從原理層面帶你深入學習下Hash演算法。

一、散列的概念

散列方法的主要想法是根據結點的關鍵碼值來確定其儲存位址：以關鍵碼值K為自變量，透過一定的函數關係h(K)(稱為散列函數)，計算出對應的函數值來，把這個值解釋為結點的存儲地址，將結點存入到此存儲單元中。檢索時，用同樣的方法計算地址，然後到對應的單元去取要找的結點。透過散列方法可以對結點進行快速檢索。雜湊（hash，也稱為“哈希”）是一種重要的儲存方式，也是一種常見的檢索方法。

以雜湊儲存方式建構的儲存結構稱為散列表（hash table）。散列表中的一個位置稱為槽(slot)。雜湊技術的核心是雜湊函數(hash function)。對任意給定的動態查找表DL，如果選取了某個「理想的」雜湊函數h及對應的散列表HT，則對DL中的每個資料元素X。函數值h（X.key）就是X在散列表HT中的儲存位置。插入（或建表）時資料元素X將被安置在該位置上，並且檢索X時也到該位置上去查找。由雜湊函數決定的儲存位置稱為雜湊位址。因此，雜湊的核心是：由雜湊函數決定關鍵碼值(X.key)與雜湊位址h(X.key)之間的對應關係，透過這種關係來實現組織儲存並進行檢索。

一般情況下，散列表的儲存空間是一個一維陣列HT[M]，雜湊位址是陣列的下標。設計雜湊方法的目標，就是設計某個雜湊函數h，0<=h( K ) < M；對於關鍵碼值K，得到HT[i] = K。在一般情況下，散列表的空間必須比結點的集合大，此時雖然浪費了一定的空間，但換取的是檢索效率。設散列表的空間大小為M，填入表中的結點數為N，則稱為散列表的負載因子（load factor，也有人翻譯為「裝填因子」）。建立散列表時，若關鍵碼與雜湊位址是一對一的關係，則在檢索時只需根據雜湊函數對給定值進行某種運算，即可得到待查結點的儲存位置。但是，雜湊函數可能對於不相等的關鍵碼計算出相同的雜湊位址，我們稱該現象為衝突（collision），發生衝突的兩個關鍵碼稱為該雜湊函數的同義詞。在實際應用中，很少存在不產生衝突的雜湊函數，我們必須考慮在衝突發生時的處理辦法。

二、雜湊函數

在以下的討論中，我們假設處理的是值為整數的關鍵碼，否則我們總是可以建立一個關鍵碼與正整數之間的一一對應關係，從而將該關鍵碼的檢索轉換為對與其對應的正整數的檢索；同時，進一步假定雜湊函數的值落在0到M－1之間。雜湊函數的選取原則是：運算盡可能簡單；函數的值域必須在散列表的範圍內；盡可能使得結點均勻分佈，也就是盡量讓不同的關鍵碼具有不同的雜湊函數值。需要考慮各種因素：關鍵碼長度、散列表大小、關鍵碼分佈、記錄的檢索頻率等等。下面我們介紹幾種常用的雜湊函數。

1.除餘法

顧名思義，除餘法就是用關鍵碼x除以M（往往取散列表長度），並取餘數作為雜湊位址。除餘法幾乎是最簡單的雜湊方法，雜湊函數為：h(x) ＝ x mod M。

2.當餘取整法

使用此方法時，先讓關鍵碼key乘以一個常數A (0< A < 1)，提取乘積的小數部分。然後，再用整數n乘以這個值，對結果向下取整，把它做為散列的位址。雜湊函數為：hash ( key ) = _LOW( n × ( A × key % 1 ) )。其中，「A × key % 1」表示取A × key 小數部分，即：A × key % 1 = A × key - _LOW(A × key), 而_LOW(X)是表示對X取下整

3.平方取中法

由於整數相除的運行速度通常比相乘慢，所以有意識地避免使用除餘法運算可以提高雜湊演算法的運行時間。平方取中法的具體實現是：先透過求關鍵碼的平方值，從而擴大相近數的差別，然後根據表長度取中間的幾位數（往往取二進制的比特位）作為散列函數值。因為一個乘積的中間幾位數與乘數的每一數位都相關，所以所產生的雜湊位址較為均勻。

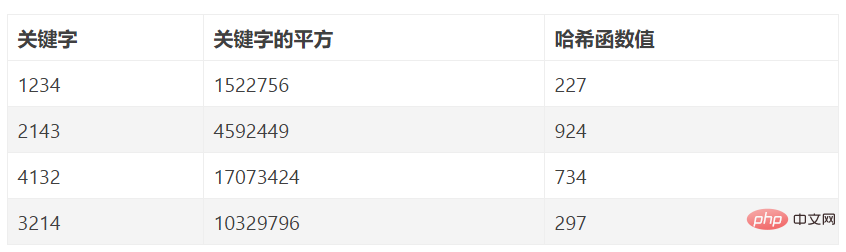
4.數字分析法

#假設關鍵字集合中的每個關鍵字都是由s 位數字組成(u1, u2, …, us)，分析關鍵字集中的全體，並從中提取分佈均勻的若干位或它們的組合作為地址。數字分析法是取資料元素關鍵字中某些取值較均勻的數字位元作為雜湊位址的方法。即當關鍵字的位數很多時，可以透過對關鍵字的各位進行分析，丟掉分佈不均勻的位，作為雜湊值。它只適合所有關鍵字值已知的情況。透過分析分佈情形把關鍵字取值區間轉換成一個較小的關鍵字取值區間。

舉個例子：要建構一個資料元素個數n=80,雜湊長度m=100的雜湊表。不失一般性，我們這裡只給其中8個關鍵字進行分析，8個關鍵字如下所示：

K1=61317602 K2=61326875 K3=62739628 K4=61343634

K5=62706815 K6=62774638 K7=61381262 K8=61394220

分析上述8個關鍵字可知，關鍵字由左至右的第1、2、3、6位元取值比較集中，不宜為哈希位址，剩餘的第4、5、7、8位元取值較均勻，可選取其中的兩位作為哈希位址。設選取最後兩位為哈希位址，則這8個關鍵字的雜湊位址分別為：2，75，28，34，15，38，62，20。

此法適合：能預先估計出全體關鍵字的每一位上各種數字出現的頻度。

5.基數轉換法

將關鍵碼值看成另一種進位的數再轉換成原來進位的數，然後選其中幾位作為雜湊地址。

例Hash(80127429)=(80127429)13=8137 0136 1135 2134 7133 4132 2*131 9=(502432641)10若取中間三位數 為了獲得良好的雜湊函數，可以將幾種方法聯合起來使用，例如先變基，再折疊或平方取中等等，只要散列均勻，就可以隨意拼湊。

6.折疊法

有時關鍵碼所含的位數很多，採用平方取中法計算太複雜，則可將關鍵碼分割成位數相同的幾部分（最後一部分的位數可以不同），然後取這幾部分的疊加和（捨去進位）作為雜湊位址，這方法稱為折疊法。

分為：

• 移位疊加：將分割後的幾部分低位元對齊相加。
• 邊界疊加:從一端沿著分割界來回折疊，然後對齊相加。

三、衝突解決的策略

儘管雜湊函數的目標是使得衝突最少，但實際上衝突是無法避免的。因此，我們必須研究衝突解決策略。衝突解決技術可以分為兩類：開散列方法( open hashing，也稱為拉鍊法，separate chaining )和閉散列方法( closed hashing，也稱為開地址方法，open addressing )。這兩種方法的不同之處在於：開散列法把發生衝突的關鍵碼存放在散列表主表之外，而閉散列法把發生衝突的關鍵碼存放在表中另一個槽內。

1.分離鍊錶法

(1)拉鍊法

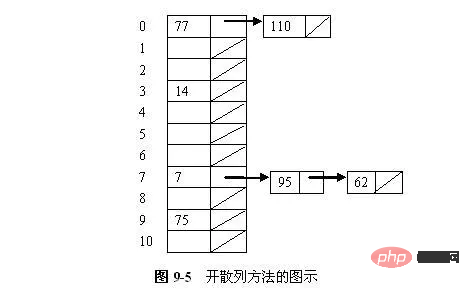
開散列方法的一種簡單形式是把散列表中的每個槽定義為一個鍊錶的表頭。散列到一個特定槽的所有記錄都放到這個槽的鍊錶中。圖9-5說明了一個開散列的散列表，這個表中每一個槽儲存一個記錄和一個指向鍊錶其餘部分的指標。這7個數儲存在有11個槽的散列表中，使用的雜湊函數是h(K) = K mod 11。數的插入順序是77、7、110、95、14、75和62。有2個值散列到第0個槽，1個值散列到第3個槽，3個值散列到第7個槽，1個值散列到第9個槽。

2.閉散列方法(開放位址法)

閉散列方法把所有記錄直接儲存在散列表中。每個記錄關鍵碼key有一個由雜湊函數計算出來的基底位置，即h(key)。如果要插入一個關鍵碼，而另一個記錄已經佔據了R的基底位置(發生碰撞)，那麼就把R儲存在表中的其它位址內，由衝突解決策略決定是哪個位址。

閉散列表解決衝突的基本想法是：當衝突發生時，使用某種方法為關鍵碼K產生一個雜湊位址序列d0，d1，d2，... di ，...dm -1。其中d0=h（K）稱為K的基底位址地置( home position )；所有di(0< i< m)是後繼雜湊位址。當插入K時，若基底位址上的結點已被別的資料元素佔用，則按上述位址序列依序探查，將找到的第一個開放的空閒位置di作為K的儲存位置；若所有後繼雜湊地址都不空閒，說明該閉散清單已滿，報告溢位。相應地，檢索K時，將按同值的後繼地址序列依次查找，檢索成功時返回該位置di ；如果沿著探查序列檢索時，遇到了開放的空閒地址，則說明表中沒有待查的關鍵碼。刪除K時，也按同值的後繼位址序列依序查找，查找到某個位置di具有該K值，則刪除該位置di上的資料元素（刪除操作實際上只是對該結點加以刪除標記）；如果遇到了開放的空閒位址，則表示表中沒有待刪除的關鍵碼。因此，對於閉散列表來說，建構後繼雜湊位址序列的方法，也就是處理衝突的方法。

形成探查的方法不同，所得到的解決衝突的方法也不同。下面是幾種常見的構造方法。

(1)線性探測法

將散列表看成是環形表，若在基底位址d（即h(K)=d）發生衝突，則依序探查下述位址單元：d 1，d 2，......，M-1，0，1，......，d-1直到找到一個空閒位址或查找到關鍵碼為key的結點為止。當然，若沿著該探查序列檢索一遍之後，又回到了位址d，則無論是做插入操作還是做檢索操作，都意味著失敗。用於簡單線性探查的探查函數是：p(K，i) = i

例9.7 已知一組關鍵碼為（26，36，41，38，44，15，68，12，06，51，25），散列表長度M= 15，用線性探查法解決衝突構造這組關鍵碼的散列表。因為n=11，利用除餘法建構雜湊函數，選取小於Ｍ的最大質數P=13，則雜湊函數為：h(key) = key 。依序插入各個結點：26: h(26) = 0，36: h(36) = 10， 41: h(41) = 2，38: h(38) = 12， 44: h(44) = 5。插入15時，其雜湊位址為2，由於2已被關鍵碼為41的元素佔用，故需進行探查。依序探查法，顯然3為開放的空閒地址，故可將其放在3單元。類似地，68和12可分別放在4和13單元中.

(2)二次探查法

二次探查法的基本思想是：產生的後繼雜湊位址不是連續的，而是跳躍式的，以便為後續資料元素留下空間從而減少聚集。二次探查法的探查序列依序為：12，-12，22 ，-22，...等，也就是說，發生衝突時，將同義詞來回散列在第一個位址的兩端。求下一個開放位址的公式為：

#(3)隨機探查法

################### #理想的探查函數應在探查序列中隨機地從未訪問過的槽中選擇下一個位置，即探查序列應是散列表位置的一個隨機排列。但是，我們實際上不能隨機地從探查序列中選擇一個位置，因為在檢索關鍵碼的時候不能建立起同​​樣的探查序列。然而，我們可以做一些類似偽隨機探查( pseudo-random probing )的事情。在偽隨機探查中，探查序列中的第i個槽是(h(K) ri) mod M，其中ri是1到M - 1之間數的「隨機」數序列。所有插入和檢索都使用相同的“隨機”數。探查函數將是 p(K，i) = perm[i - 1]， 這裡perm是長度為M - 1的數組，它包含值從1到M – 1的隨機序列。 ######範例：######例如，已知雜湊表長度m=11，雜湊函數為：H（key）= key % 11，則H（47）=3，H（ 26）=4，H（60）=5，假設下一個關鍵字為69，則H（69）=3，與47衝突。如果用線性探測再雜湊處理衝突，下一個雜湊位址為H1=（3 1）% 11 = 4，仍然衝突，再找下一個雜湊位址為H2=（3 2）% 11 = 5，還是衝突，繼續找下一個哈希位址為H3=（3 3）% 11 = 6，此時不再衝突，將69填入5號單元，參考圖8.26 (a)。如果用二次探測再雜湊處理衝突，下一個雜湊位址為H1=（3 12）% 11 = 4，仍然衝突，再找下一個雜湊位址為H2=（3 - 12）% 11 = 2 ，此時不再衝突，將69填入2號單元，參考圖8.26 (b)。如果用偽隨機探測再散列處理衝突，且偽隨機數序列為：2，5，9，……..，則下一個哈希地址為H1=（3 2）% 11 = 5，仍然衝突，再找下一個雜湊位址為H2=（3 5）% 11 = 8，此時不再衝突，將69填入8號單元，參考圖8.26 (c)。 ##################(4)雙散列探查法#######

偽隨機探查和二次探查都能消除基本聚集－即基底位址不同的關鍵碼，其探查序列的某些段落重疊在一起－的問題。然而，如果兩個關鍵碼雜湊到同一個基底位址，那麼採用這兩種方法還是得到同樣的探查序列，仍然會產生聚集。這是因為偽隨機探查和二次探查產生的探查序列只是基底位址的函數，而不是原來關鍵碼值的函數。這個問題稱為二級聚集( secondary clustering )。

為了避免二級聚集，我們需要使得探查序列是原來關鍵碼值的函數，而不是基底位置的函數。雙散列探查法利用第二個雜湊函數作為常數，每次跳過常數項，做線性探查。

#

以上是每天都用！你了解HASH是什麼東東嗎？的詳細內容。更多資訊請關注PHP中文網其他相關文章！