70年前他想逃避考試，卻影響了整個互聯網

谁曾想，一次学生不想参加考试的“任性”，后来竟影响了整个互联网。

70年前MIT的一堂信息论课上，一位老师为了给学生“减压”，摆出一道选择题。

要么参加期末考试，要么写篇论文改进现有算法，自己挑。

这位老师名叫罗伯特·范诺，他没告诉学生们的是，这个“现有算法”，正是他和信息论创始人香农合著的香农-范诺编码。而为了改进算法不足，他本人已经投入大量时间进行研究。

（老师内心OS：没想到吧。）

虽然有点损，但这招还真管用。这票学生一听“交篇论文”就不用考试，拍脑袋就决定写论文，包括大卫•哈夫曼。

不选不知道，一选吓一跳。初出茅庐的哈夫曼很快意识到了老师挖的坑——这论文也太**难搞了。

这一写，就是好几个月，并且苦苦挣扎中，哈夫曼仍然一无所获。

但命运，有时候就是十分奇妙。就在哈夫曼终于放弃“逃考”，准备将论文笔记扔到垃圾桶中时，突然灵光一现！答案出现了！

哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的方法。

他提出的这一想法，效率成功超越他老师的方法论。甚至在之后的发展中，以他命名的编码方法——哈夫曼编码，直接改变了数据压缩范式。

至于当时那篇结题报告，已引用近万次。

低效的传统编码方法

1951年，正在MIT任教的罗伯特·范诺正在思考一道信息论的难题：

如何用二进制代码高效表示数字、字母或者其他符号？

当时最常见、也是最直接的方法，就是为每个字符分配一个独一无二的二进制数。

比如，字母A可能表示为01000001，！表示为 00100001，每个八位数的数字都对应一个字符。

这样一来代码容易解析，但效率极低。

另外还有种优化方法，类似于摩尔斯电码。常用字母E仅由一个点表示，但不常见的Q需要更长且更费力的“—— —— · ——”。

这种方式，会导致代码长度不一， 信息不容易被理解；而且传输中还需要在字符间加入间隙，否则就无法区分不同的字符组合。

范诺意识到，或许这两种方法的优势可以兼并之——以不同长度的二进制代码表示字符。进一步地，为避免代码“重叠”，他还构建了二叉树。

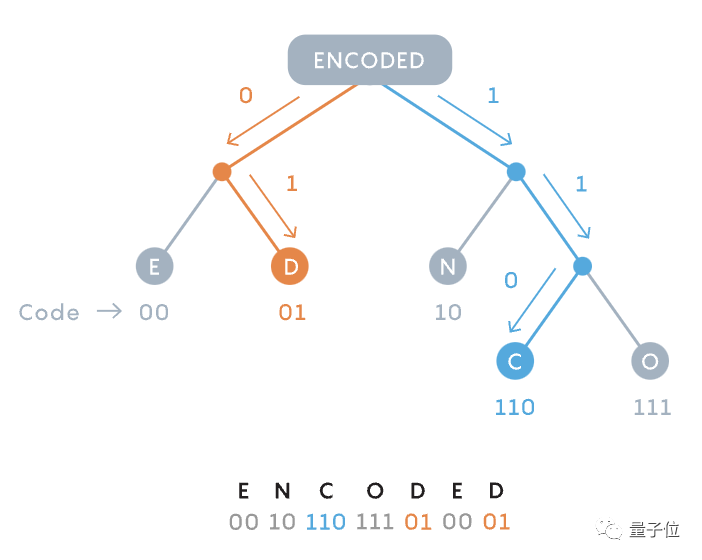图片

他详尽地测试了每一种排列的可能性以获得最大效率，最终得到了一种有效情况：

每条消息按照频率分为两个分支，并尽可能让两边字母使用频率基本相同。

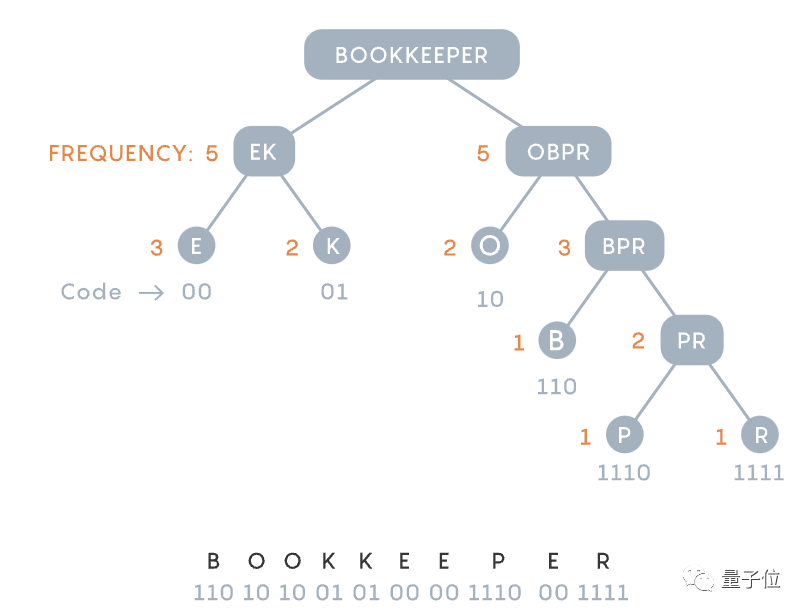图片

这样，常用的字符就会在更短、密度更低的分支上。

1948年，信息论之父香农在介绍信息理论的文章“通信数学理论”中提出了这一方法；不久之后，范诺也独立地以技术报告形式将其发布。故而这套方法被称作是香农-范诺编码。

但这个方法并非总是有效。像字母出现概率分别为{0.35，0.17，0.17，0.16，0.15}这种情况时，就不能给出理想编码。

范诺认为一定存在更好压缩策略。于是乎，这样的重任就交到了他的学生手里。

一次灵光乍现，一篇世纪论文

如果说，范诺教授他们的方法是从上到下构建字符树，并在成对的树枝之间尽可能保持对称。

那么哈夫曼的方法，是直接颠覆了这一过程——自下而上构建二叉树。

他认为，无论发生什么情况，在一段有效的代码中，两个最不常见的字符应该有两个最长的代码。

因此首先就确定两个最不常见的字符，将它们组合在一起作为一个分支对，然后再重复该过程，再从剩余字符中与刚刚构建的字符对中寻找最不常见的字符（对）。

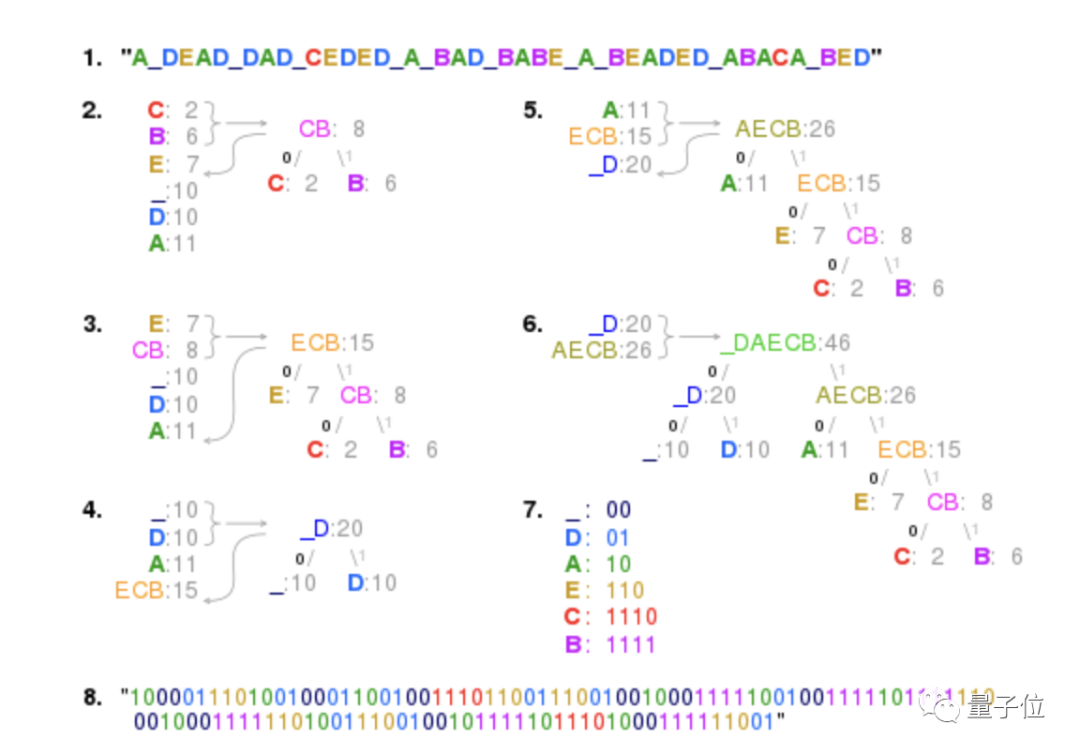圖片

以schoolroom為例，其中O出現了四次，S、C、H、L、R、M各出現一次。

範諾的方法，就是先將O與另一個字母分配給左側分支，這樣一來兩邊都是5次總使用量，生成的編碼總共27位。

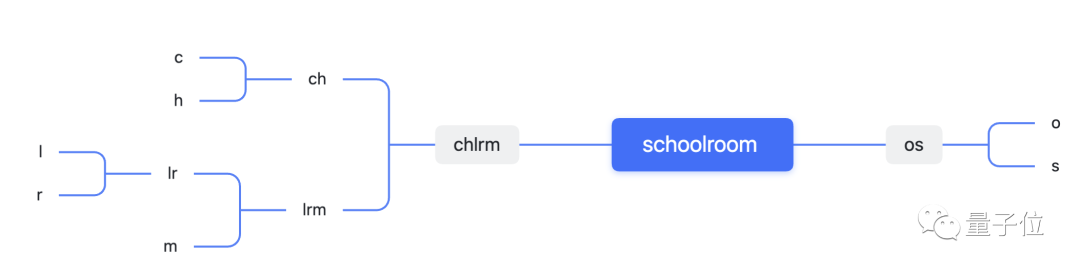圖片

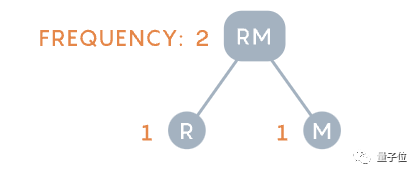
相比之下，哈夫曼的方法，例如就從不常見的r和m開始，將其組合成一個字母對。

圖片

組合完後，現有字元（對）包括：O（4次）、RM（2次）以及單一字母S、 C、H和L。

依照出現頻率劃分，重複上一操作－將兩個不常見的選項分組，然後更新數樹和頻率圖。

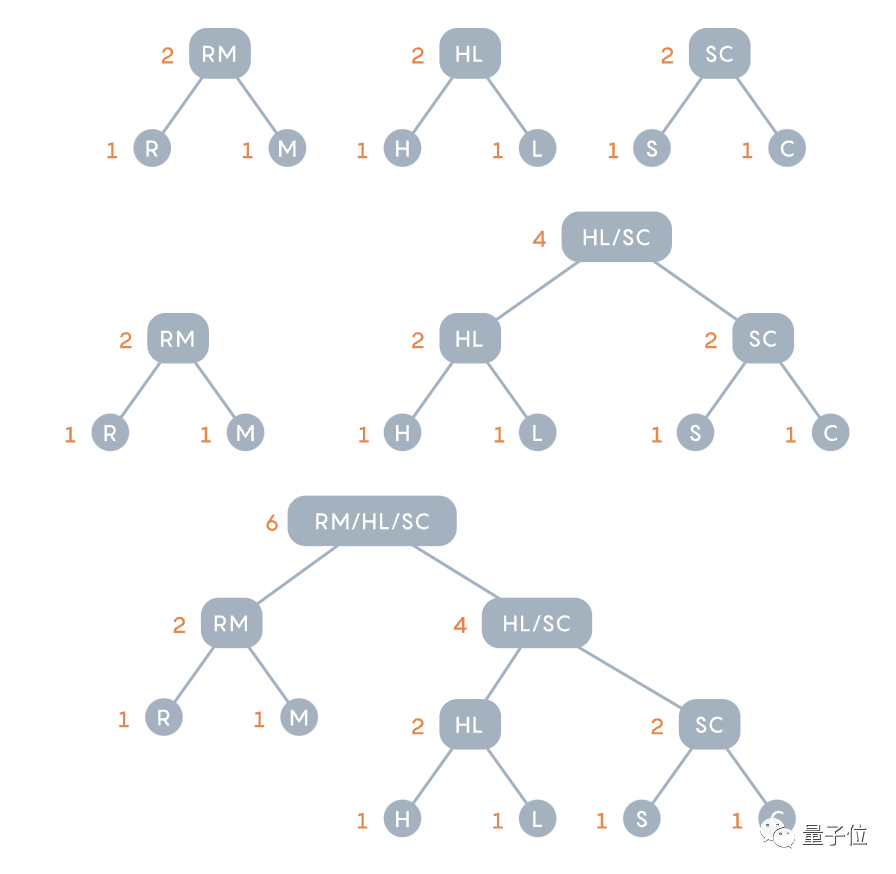
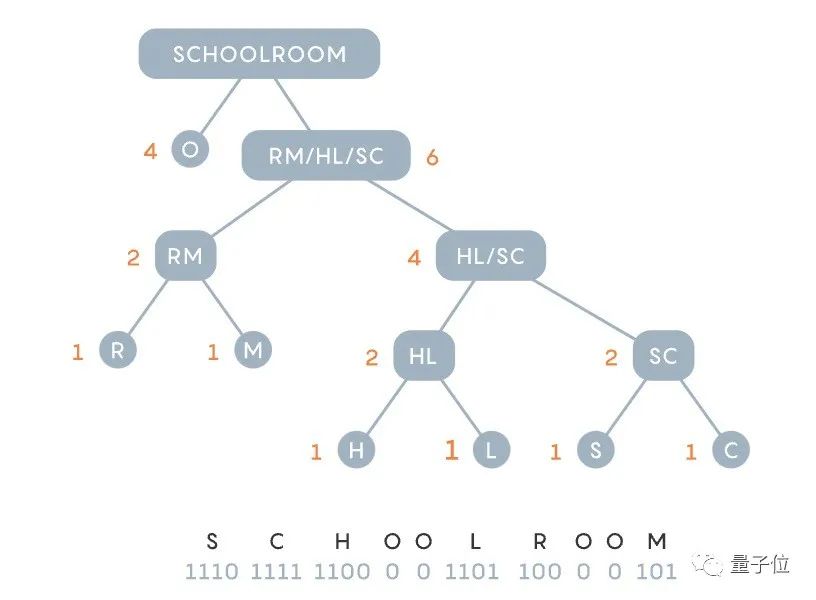
最終，「schoolroom」變成了 111011111110000110110000101，比Fano 自上而下的方法少了1位元。  

圖片

雖然1位元在這裡並不多，但要是當擴展到數十億位元組時候，這就是一次不小的節省。

事實上，哈夫曼的方法已經被證明非常強大，根據Google學術統計，當年論文已經被引用9570次。

圖片

至於他老師的辦法，卻幾乎沒有再被使用過。

直到今天，幾乎所有無損壓縮方法都全部或部分使用了哈夫曼的方法，可以壓縮影像、音訊、表格等。它支援從PNG圖像標準到無處不在的軟體PKZip 的一切。

現代電腦科學先驅、圖靈獎得主高德納曾這樣形容哈夫曼的成就：

在電腦科學和數據通訊領域，哈夫曼編碼是人們一直在使用的基本思想。

後來哈夫曼再回想起那個「靈光乍現」時刻，當時他正準備將論文筆記丟進垃圾桶，結果突然思想匯聚，答案在腦海裡出現了：

那是我生命中最奇特的時刻。

突然恍然大悟，就如閃電一般。

並表示，如果他知道自己的教授範諾(Fano)曾與這個問題作過鬥爭，他可能永遠不會嘗試解決這個問題，更不用說在25歲的時候就大膽去嘗試。

成就與秩序感，用數學玩藝術

哈夫曼編碼改變了資料壓縮範式，也為其贏得了許多榮譽與獎章。

例如，1998年哈夫曼獲得IEEE 資訊理論學會頒發的技術創新金禧獎、1999年獲得電氣和電子工程師協會(IEEE) 頒發的理查德·漢明獎章（Richard Hamming Medal ）。

不過即便如此，在他一生歷程中，相比發明無損壓縮方法這件事兒，最讓他引以為傲的反而是這篇博士論文。

主題：The Synthesis of Sequential Switching Circuits。

圖片

哈夫曼在MIT讀博期間，發布這篇討論時序開關電路的重要論文。在當時，哈夫曼幾乎是首個闡述如何設計非同步順序開關電路的學者，而這個理論後來也為電腦發展提供了重要邏輯支撐。

這篇論文的發布，不僅幫助他獲得富蘭克林研究所的Louis E. Levy Medal，也順理成章讓他獲得留校任職資格，教授關於開關電路的課程。

圖片

在學校期間，哈夫曼也提出一種革新的數學公式，可以在不遺失任何資訊的情況下將一個二進制數序列轉換成另一個二進制數序列，這項研究在當時發揮了重要作用，也為其謀得了一份重要職位。

時任貝爾實驗室研究副總裁的William O. Baker將其招納入了一個審查委員會，主要負責為國家安全局審查未來科技計劃。 Baker博士曾擔任艾森豪威爾、甘迺迪、約翰遜、尼克森和雷根五位總統的科學顧問。

1967年已是正教授的霍夫曼選擇離開MIT，加入加州大學聖克魯茲分校(UCSC)，期間主導創立了電腦科學系，並參與學術課程開發工作，為之後電腦科學系發展奠定重要基礎。

數學可以說是哈夫曼畢生追求之一，以至於後來在搞藝術時，也離不開數學。

圖片

70年代開始，哈夫曼對摺紙產生濃厚興趣，同時研究數學和摺紙藝術，製作了上百件曲痕摺紙作品，也特別發表論文分析曲痕摺紙的數學性質，成為摺紙數學領域的先驅人物。

回過頭看，哈夫曼的一生贏得無數榮譽與表彰，卻從未為自己任何一項發明申請過專利。

最後，借用哈夫曼自己的一段話。

身為科學家和老師，我真的非常執著。如果我覺得自己還沒有找到問題的最簡單解決方法，我會非常不滿意，這種不滿會一直持續，直到我找到最佳方法。對我來說，這就是科學家的本質。

以上是70年前他想逃避考試，卻影響了整個互聯網的詳細內容。更多資訊請關注PHP中文網其他相關文章！