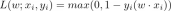梯度下降是機器學習的動力之源
經過前面兩節內容的鋪墊,我們可以開始講一講機器學習的動力之源:梯度下降。
梯度下降並不是一個很複雜的數學工具,其歷史已經有200多年了,但是人們可能不曾料到,這樣一個相對簡單的數學工具會成為諸多機器學習演算法的基礎,而且還配合著神經網路點燃了深度學習革命。
1、什麼是梯度
對多元函數的各參數求偏導數,然後把所求得的各個參數的偏導數以向量的形式寫出來,就是梯度。
具體來說,兩個自變數的函數f(x1,x2),對應機器學習資料集中的兩個特徵,如果分別對x1,x2求偏導數,那麼求得的梯度向量就是(∂f/∂x1,∂f/∂x2)T,在數學上可以表示成Δf(x1,x2)。那麼計算梯度向量的意義何在呢?其幾何意義,就是函數變化的方向,而且是變化最快的方向。對於函數f(x),在點(x0,y0),梯度向量的方向也就是y值增加最快的方向。也就是說,沿著梯度向量的方向Δf(x0),可以找出函數的最大值。反過來說,沿著梯度向量相反的方向,也就是 -Δf(x0)的方向,梯度減少最快,能找到函數的最小值。如果某點的梯度向量的值為0,那麼也就是來到了導數為0的函數最低點(或局部最低點)了。
2、梯度下降:下山的隱喻
在機器學習中用下山來比喻梯度下降是很常見的。想像你們站在一座大山上某個地方,看著遠處的地形,一望無際,只知道遠處的位置比這裡低很多。你們想知道如何下山,但是只能一步一步往下走,那也就是在每走到一個位置的時候,求解當前位置的梯度。然後,沿著梯度的負方向,也就是往最陡峭的地方向下走一步,繼續求解新位置的梯度,並在新位置繼續沿著最陡峭的地方向下走一步。就這樣一步步走,直到山腳,如下圖。

從上面的解釋中,就不難理解為何剛才我們要提到函數的凹凸性了。因為,在非凸函數中,有可能還沒走到山腳,而是到了某一個山谷就停了下來。也就是說,對應非凸函數梯度下降不一定總是能找到全域最優解,有可能得到的只是一個局部最優解。然而,如果函數是凸函數,那麼梯度下降法理論上就能得到全域最優解。
3、梯度下降有什麼用
梯度下降在機器學習中非常有用。簡單地說,可以注意以下幾點。
機器學習的本質是找到最優的函數。
如何衡量函數是否最優?其方法是盡量減少預測值和真值間的誤差(在機器學習中也叫損失值)。
可以建立誤差和模型參數之間的函數(最好是凸函數)。
梯度下降能夠引導我們走到凸函數的全域最低點,也就是找到誤差最小時的參數。
以上是一文帶你了解什麼是梯度下降的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM
優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM介紹 恭喜!您經營一家成功的業務。通過您的網頁,社交媒體活動,網絡研討會,會議,免費資源和其他來源,您每天收集5000個電子郵件ID。下一個明顯的步驟是
 Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM
Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM介紹 在當今快節奏的軟件開發環境中,確保最佳應用程序性能至關重要。監視實時指標,例如響應時間,錯誤率和資源利用率可以幫助MAIN
 Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM“您有幾個用戶?”他扮演。 阿爾特曼回答說:“我認為我們上次說的是每週5億個活躍者,而且它正在迅速增長。” “你告訴我,就像在短短幾週內翻了一番,”安德森繼續說道。 “我說那個私人
 pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介紹 Mistral發布了其第一個多模式模型,即Pixtral-12b-2409。該模型建立在Mistral的120億參數Nemo 12B之上。是什麼設置了該模型?現在可以拍攝圖像和Tex
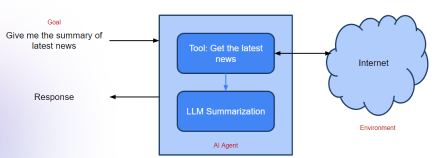 生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想像一下,擁有一個由AI驅動的助手,不僅可以響應您的查詢,還可以自主收集信息,執行任務甚至處理多種類型的數據(TEXT,圖像和代碼)。聽起來有未來派?在這個a


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境

SublimeText3 英文版
推薦:為Win版本,支援程式碼提示!

DVWA
Damn Vulnerable Web App (DVWA) 是一個PHP/MySQL的Web應用程序,非常容易受到攻擊。它的主要目標是成為安全專業人員在合法環境中測試自己的技能和工具的輔助工具,幫助Web開發人員更好地理解保護網路應用程式的過程,並幫助教師/學生在課堂環境中教授/學習Web應用程式安全性。 DVWA的目標是透過簡單直接的介面練習一些最常見的Web漏洞,難度各不相同。請注意,該軟體中

SublimeText3漢化版
中文版,非常好用

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能