Python怎麼實現低通濾波器模糊影像功能

使用低通濾波器模糊圖像

0. 前言

低通濾波器(Low Pass Filter, LPF) 過濾了影像中的高頻部分，並僅允許低頻部分通過。因此，在影像上套用LPF 會刪除影像中的細節/邊緣和雜訊/離群值，此過程也稱為影像模糊(或平滑)，影像平滑可以作為複雜影像處理任務的預處理部分。

1. 頻域中的不同類型的核與卷積

1.1 影像模糊分類

影像模糊通常包含以下類型：

• 邊緣模糊(Edge) 這種類型的模糊通常透過卷積明確地應用於影像，例如線性濾波器核或高斯核等，使用這些濾波器核可以平滑/去除影像中不必要的細節/雜訊。

• 動作模糊 (Motion) 通常是因為相機在拍攝影像時會抖動所產生的，也就是說，攝影機或被拍攝的物件處於移動狀態。我們可以使用點擴展函數來模擬這種模糊。

• 失焦模糊(de-focus) 當相機拍攝的物件失焦時，會產生這種類型的模糊；我們可以使用模糊(blur) 核來模擬這種模糊。

接下來，我們建立以上三種不同類型的核，並將它們應用於影像以觀察不同類型核處理影像後的結果。

1.2 使用不同核心執行影像模糊

(1) 我們先定義函數get_gaussian_edge_blur_kernel() 以傳回2D高斯模糊核用於邊緣模糊。此函數接受高斯標準差( σ σ σ) 以及創建2D 核的大小(例如，sz = 15 將建立尺寸為15x15 的核)作為函數的參數。如下所示，首先建立了一個1D 高斯核，然後計算兩個1D 高斯核的外積回傳2D 核：

import numpy as np
import numpy.fft as fp
from skimage.io import imread
from skimage.color import rgb2gray 
import matplotlib.pyplot as plt
import cv2

def get_gaussian_edge_blur_kernel(sigma, sz=15):
    # First create a 1-D Gaussian kernel
    x = np.linspace(-10, 10, sz)
    kernel_1d = np.exp(-x**2/sigma**2)
    kernel_1d /= np.trapz(kernel_1d) # normalize the sum to 1.0
    # create a 2-D Gaussian kernel from the 1-D kernel
    kernel_2d = kernel_1d[:, np.newaxis] * kernel_1d[np.newaxis, :]
    return kernel_2d

(2) 接下來，定義函數get_motion_blur_kernel() 以產生運動模糊核，得到給定長度且特定方向(角度)的線作為卷積核，以模擬輸入影像的運動模糊效果：

def get_motion_blur_kernel(ln, angle, sz=15):
    kern = np.ones((1, ln), np.float32)
    angle = -np.pi*angle/180
    c, s = np.cos(angle), np.sin(angle)
    A = np.float32([[c, -s, 0], [s, c, 0]])
    sz2 = sz // 2
    A[:,2] = (sz2, sz2) - np.dot(A[:,:2], ((ln-1)*0.5, 0))
    kern = cv2.warpAffine(kern, A, (sz, sz), flags=cv2.INTER_CUBIC)
    return kern

函數get_motion_blur_kernel() 將模糊的長度和角度以及模糊核的尺寸作為參數，函數使用OpenCV 的 warpaffine() 函數傳回核矩陣(以矩陣中心為中點，使用給定長度和給定角度得到核)。

(3) 最後，定義函數get_out_of_focus_kernel() 以產生失焦核(模擬影像失焦模糊)，其根據給定半徑建立圓形用作卷積核，函數接受半徑R (Deocus Radius) 和要產生的核大小作為輸入參數：

 def get_out_of_focus_kernel(r, sz=15):
    kern = np.zeros((sz, sz), np.uint8)
    cv2.circle(kern, (sz, sz), r, 255, -1, cv2.LINE_AA, shift=1)
    kern = np.float32(kern) / 255
    return kern

(4) 接下來，實作函數dft_convolve()，該函數使用影像的逐元素乘法和頻域中的捲積核執行頻域卷積(基於卷積定理)。函數也繪製輸入影像、核和卷積計算後得到的輸出影像：

def dft_convolve(im, kernel):
    F_im = fp.fft2(im)
    #F_kernel = fp.fft2(kernel, s=im.shape)
    F_kernel = fp.fft2(fp.ifftshift(kernel), s=im.shape)
    F_filtered = F_im * F_kernel
    im_filtered = fp.ifft2(F_filtered)
    cmap = 'RdBu'
    plt.figure(figsize=(20,10))
    plt.gray()
    plt.subplot(131), plt.imshow(im), plt.axis('off'), plt.title('input image', size=10)
    plt.subplot(132), plt.imshow(kernel, cmap=cmap), plt.title('kernel', size=10)
    plt.subplot(133), plt.imshow(im_filtered.real), plt.axis('off'), plt.title('output image', size=10)
    plt.tight_layout()
    plt.show()

(5) 將get_gaussian_edge_blur_kernel() 核函數套用至影像，並繪製輸入，核和輸出模糊圖像：

im = rgb2gray(imread('3.jpg'))

kernel = get_gaussian_edge_blur_kernel(25, 25)
dft_convolve(im, kernel)

(6) 接下來，將get_motion_blur_kernel() 函數應用於圖像，並繪製輸入，核和輸出模糊影像：

kernel = get_motion_blur_kernel(30, 60, 25)
dft_convolve(im, kernel)

(7) 最後，將get_out_of_focus_kernel() 函數套用至影像，並繪製輸入，核和輸出模糊影像：

kernel = get_out_of_focus_kernel(15, 20)
dft_convolve(im, kernel)

2. 使用scipy.ndimage 濾波器模糊圖像

scipy.ndimage 模組提供了一系列可以在頻域中對圖像應用低通濾波器的函數。在本節中，我們透過幾個範例學習其中一些濾波器的用法。

2.1 使用fourier_gaussian() 函數

使用scipy.ndimage 庫中的fourier_gaussian() 函數在頻域中使用高斯核執行卷積操作。

(1) 首先，讀取輸入影像，並將其轉換為灰階影像，並透過使用FFT 取得其頻域表示：

import numpy as np
import numpy.fft as fp
from skimage.io import imread
import matplotlib.pyplot as plt
from scipy import ndimage

im = imread('1.png', as_gray=True)
freq = fp.fft2(im)

(2) 接下來，使用fourier_gaussian() 函數對影像執行模糊操作，使用兩個具有不同標準差的高斯核，繪製輸入、輸出影像以及功率譜：

fig, axes = plt.subplots(2, 3, figsize=(20,15))
plt.subplots_adjust(0,0,1,0.95,0.05,0.05)
plt.gray() # show the filtered result in grayscale
axes[0, 0].imshow(im), axes[0, 0].set_title('Original Image', size=10)
axes[1, 0].imshow((20*np.log10( 0.1 + fp.fftshift(freq))).real.astype(int)), axes[1, 0].set_title('Original Image Spectrum', size=10)
i = 1
for sigma in [3,5]:
    convolved_freq = ndimage.fourier_gaussian(freq, sigma=sigma)
    convolved = fp.ifft2(convolved_freq).real # the imaginary part is an artifact
    axes[0, i].imshow(convolved)
    axes[0, i].set_title(r'Output with FFT Gaussian Blur, $\sigma$={}'.format(sigma), size=10)
    axes[1, i].imshow((20*np.log10( 0.1 + fp.fftshift(convolved_freq))).real.astype(int))
    axes[1, i].set_title(r'Spectrum with FFT Gaussian Blur, $\sigma$={}'.format(sigma), size=10)
    i += 1
for a in axes.ravel():
    a.axis('off')    
plt.show()

2.2 使用fourier_uniform() 函數

scipy.ndimage 模組的函數fourier_uniform() 實作了多維均勻傅立葉濾波器。頻率陣列與給定尺寸的方形核的傅立葉變換相乘。接下來，我們學習如何使用 LPF (均值濾波器)模糊輸入灰階影像。

(1) 首先，讀取輸入影像並使用 DFT 取得其頻域表示：

im = imread('1.png', as_gray=True)
freq = fp.fft2(im)

(2) 然后，使用函数 fourier_uniform() 应用 10x10 方形核(由功率谱上的参数指定)，以获取平滑输出：

freq_uniform = ndimage.fourier_uniform(freq, size=10)

(3) 绘制原始输入图像和模糊后的图像：

fig, (axes1, axes2) = plt.subplots(1, 2, figsize=(20,10))
plt.gray() # show the result in grayscale
im1 = fp.ifft2(freq_uniform)
axes1.imshow(im), axes1.axis('off')
axes1.set_title('Original Image', size=10)
axes2.imshow(im1.real) # the imaginary part is an artifact
axes2.axis('off')
axes2.set_title('Blurred Image with Fourier Uniform', size=10)
plt.tight_layout()
plt.show()

(4) 最后，绘制显示方形核的功率谱：

plt.figure(figsize=(10,10))
plt.imshow( (20*np.log10( 0.1 + fp.fftshift(freq_uniform))).real.astype(int))
plt.title('Frequency Spectrum with fourier uniform', size=10)
plt.show()

2.3 使用 fourier_ellipsoid() 函数

与上一小节类似，通过将方形核修改为椭圆形核，我们可以使用椭圆形核生成模糊的输出图像。

(1) 类似的，我们首先在图像的功率谱上应用函数 fourier_ellipsoid()，并使用 IDFT 在空间域中获得模糊后的输出图像：

freq_ellipsoid = ndimage.fourier_ellipsoid(freq, size=10)
im1 = fp.ifft2(freq_ellipsoid)

(2) 接下来，绘制原始输入图像和模糊后的图像：

fig, (axes1, axes2) = plt.subplots(1, 2, figsize=(20,10))
axes1.imshow(im), axes1.axis('off')
axes1.set_title('Original Image', size=10)
axes2.imshow(im1.real) # the imaginary part is an artifact
axes2.axis('off')
axes2.set_title('Blurred Image with Fourier Ellipsoid', size=10)
plt.tight_layout()
plt.show()

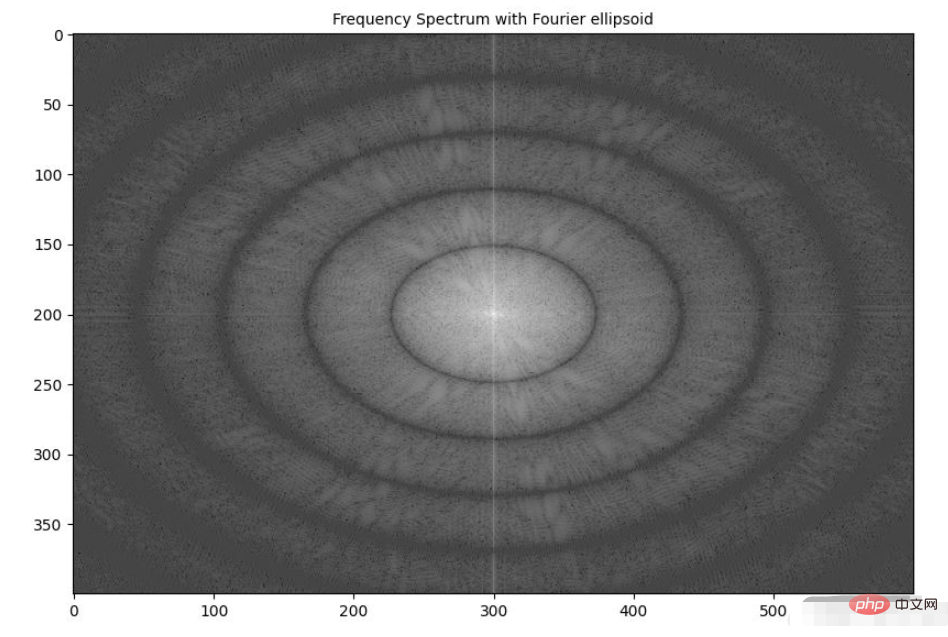
(3) 最后，显示应用椭圆形核后图像的频谱：

plt.figure(figsize=(10,10))
plt.imshow( (20*np.log10( 0.1 + fp.fftshift(freq_ellipsoid))).real.astype(int))
plt.title('Frequency Spectrum with Fourier ellipsoid', size=10)
plt.show()

3. 使用 scipy.fftpack 实现高斯模糊

我们已经学习了如何在实际应用中使用 numpy.fft 模块的 2D-FFT。在本节中，我们将介绍 scipy.fftpack 模块的 fft2() 函数用于实现高斯模糊。

(1) 使用灰度图像作为输入，并使用 FFT 从图像中创建 2D 频率响应数组：

import numpy as np
import numpy.fft as fp
from skimage.color import rgb2gray
from skimage.io import imread
import matplotlib.pyplot as plt
from scipy import signal
from matplotlib.ticker import LinearLocator, FormatStrFormatter

im = rgb2gray(imread('1.png'))
freq = fp.fft2(im)

(2) 通过计算两个 1D 高斯核的外积，在空间域中创建高斯 2D 核用作 LPF：

kernel = np.outer(signal.gaussian(im.shape[0], 1), signal.gaussian(im.shape[1], 1))

(3) 使用 DFT 获得高斯核的频率响应：

freq_kernel = fp.fft2(fp.ifftshift(kernel))

(4) 使用卷积定理通过逐元素乘法在频域中将 LPF 与输入图像卷积：

convolved = freq*freq_kernel # by the Convolution theorem

(5) 使用 IFFT 获得输出图像，需要注意的是，要正确显示输出图像，需要缩放输出图像：

im_blur = fp.ifft2(convolved).real
im_blur = 255 * im_blur / np.max(im_blur)

(6) 绘制图像、高斯核和在频域中卷积后获得图像的功率谱，可以使用 matplotlib.colormap 绘制色，以了解不同坐标下的频率响应值：

plt.figure(figsize=(20,20))
plt.subplot(221), plt.imshow(kernel, cmap='coolwarm'), plt.colorbar()
plt.title('Gaussian Blur Kernel', size=10)
plt.subplot(222)
plt.imshow( (20*np.log10( 0.01 + fp.fftshift(freq_kernel))).real.astype(int), cmap='inferno')
plt.colorbar()
plt.title('Gaussian Blur Kernel (Freq. Spec.)', size=10)
plt.subplot(223), plt.imshow(im, cmap='gray'), plt.axis('off'), plt.title('Input Image', size=10)
plt.subplot(224), plt.imshow(im_blur, cmap='gray'), plt.axis('off'), plt.title('Output Blurred Image', size=10)
plt.tight_layout()
plt.show()

(7) 要绘制输入/输出图像和 3D 核的功率谱，我们定义函数 plot_3d()，使用 mpl_toolkits.mplot3d 模块的 plot_surface() 函数获取 3D 功率谱图，给定相应的 Y 和Z值作为 2D 阵列传递：

def plot_3d(X, Y, Z, cmap=plt.cm.seismic):
    fig = plt.figure(figsize=(20,20))
    ax = fig.gca(projection='3d')
    # Plot the surface.
    surf = ax.plot_surface(X, Y, Z, cmap=cmap, linewidth=5, antialiased=False)
    #ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
    #ax.set_zscale("log", nonposx='clip')
    #ax.zaxis.set_scale('log')
    ax.zaxis.set_major_locator(LinearLocator(10))
    ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
    ax.set_xlabel('F1', size=15)
    ax.set_ylabel('F2', size=15)
    ax.set_zlabel('Freq Response', size=15)
    #ax.set_zlim((-40,10))
    # Add a color bar which maps values to colors.
    fig.colorbar(surf) #, shrink=0.15, aspect=10)
    #plt.title('Frequency Response of the Gaussian Kernel')
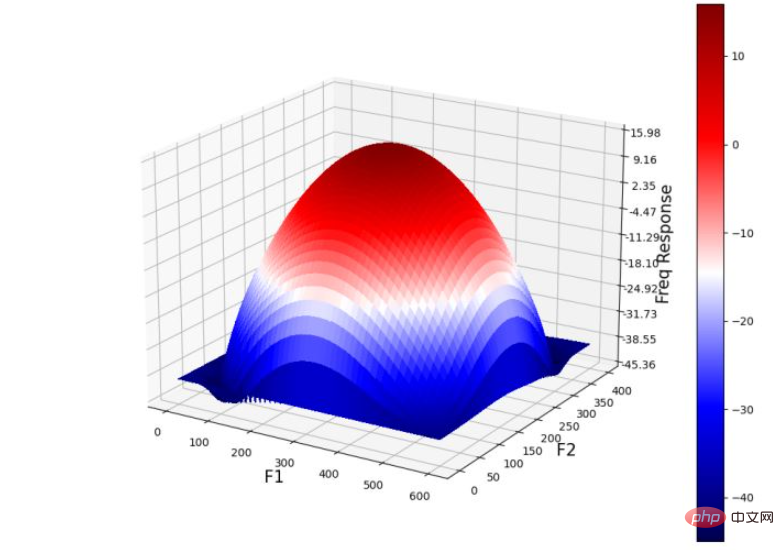
    plt.show()

(8) 在 3D 空间中绘制高斯核的频率响应，并使用 plot_3d() 函数：

Y = np.arange(freq.shape[0]) #-freq.shape[0]//2,freq.shape[0]-freq.shape[0]//2)
X = np.arange(freq.shape[1]) #-freq.shape[1]//2,freq.shape[1]-freq.shape[1]//2)
X, Y = np.meshgrid(X, Y)
Z = (20*np.log10( 0.01 + fp.fftshift(freq_kernel))).real
plot_3d(X,Y,Z)

下图显示了 3D 空间中高斯 LPF 核的功率谱：

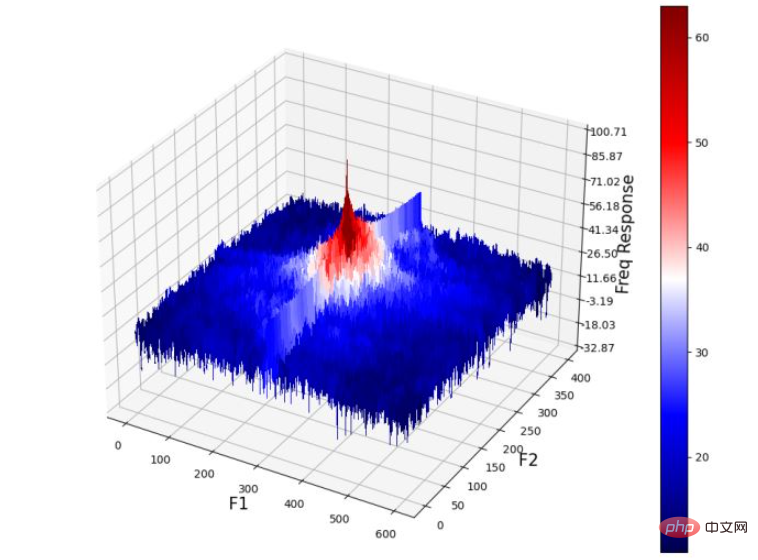
(9) 绘制 3D 空间中输入图像的功率谱：

Z = (20*np.log10( 0.01 + fp.fftshift(freq))).real
plot_3d(X,Y,Z)

(10) 最后，绘制输出图像的功率谱(通过将高斯核与输入图像卷积获得)：

Z = (20*np.log10( 0.01 + fp.fftshift(convolved))).real
plot_3d(X,Y,Z)

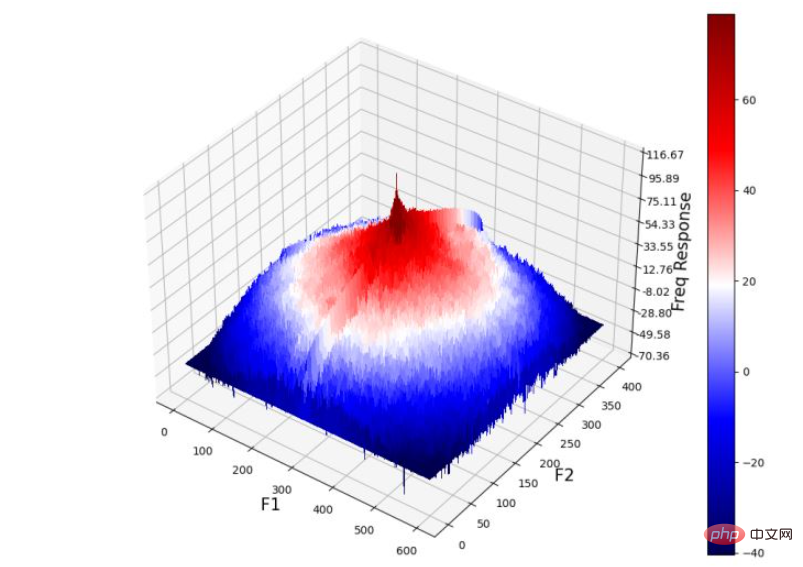
从输出图像的频率响应中可以看出，高频组件被衰减，从而导致细节的平滑/丢失，并导致输出图像模糊。

4. 彩色图像频域卷积

在本节中，我们将学习使用 scipy.signal 模块的 fftconvolve() 函数，用于与 RGB 彩色输入图像进行频域卷积，从而生成 RGB 彩色模糊输出图像：

scipy.signal.fftconvolve(in1, in2, mode='full', axes=None)

函数使用 FFT 卷积两个 n 维数组 in1 和 in2，并由 mode 参数确定输出大小。卷积模式 mode 具有以下类型：

• 输出是输入的完全离散线性卷积，默认情况下使用此种卷积模式

• 输出仅由那些不依赖零填充的元素组成，in1 或 in2 的尺寸必须相同

• 输出的大小与 in1 相同，并以输出为中心

4.1 基于 scipy.signal 模块的彩色图像频域卷积

接下来，我们实现高斯低通滤波器并使用 Laplacian 高通滤波器执行相应操作。

(1) 首先，导入所需的包，并读取输入 RGB 图像：

from skimage import img_as_float
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt

im = img_as_float(plt.imread('1.png'))

(2) 实现函数 get_gaussian_edge_kernel()，并根据此函数创建一个尺寸为 15x15 的高斯核：

def get_gaussian_edge_blur_kernel(sigma, sz=15):
    # First create a 1-D Gaussian kernel
    x = np.linspace(-10, 10, sz)
    kernel_1d = np.exp(-x**2/sigma**2)
    kernel_1d /= np.trapz(kernel_1d) # normalize the sum to 1.0
    # create a 2-D Gaussian kernel from the 1-D kernel
    kernel_2d = kernel_1d[:, np.newaxis] * kernel_1d[np.newaxis, :]
    return kernel_2d
kernel = get_gaussian_edge_blur_kernel(sigma=10, sz=15)

(3) 然后，使用 np.newaxis 将核尺寸重塑为 15x15x1，并使用 same 模式调用函数 signal.fftconvolve()：

im1 = signal.fftconvolve(im, kernel[:, :, np.newaxis], mode='same')
im1 = im1 / np.max(im1)

在以上代码中使用的 mode='same'，可以强制输出形状与输入阵列形状相同，以避免边框效应。

(4) 接下来，使用 laplacian HPF 内核，并使用相同函数执行频域卷积。需要注意的是，我们可能需要缩放/裁剪输出图像以使输出值保持像素的浮点值范围 [0,1] 内：

kernel = np.array([[0,-1,0],[-1,4,-1],[0,-1,0]])
im2 = signal.fftconvolve(im, kernel[:, :, np.newaxis], mode='same')
im2 = im2 / np.max(im2)
im2 = np.clip(im2, 0, 1)

(5) 最后，绘制输入图像和使用卷积创建的输出图像。

plt.figure(figsize=(20,10))
plt.subplot(131), plt.imshow(im), plt.axis('off'), plt.title('original image', size=10)
plt.subplot(132), plt.imshow(im1), plt.axis('off'), plt.title('output with Gaussian LPF', size=10)
plt.subplot(133), plt.imshow(im2), plt.axis('off'), plt.title('output with Laplacian HPF', size=10)
plt.tight_layout()
plt.show()

以上是Python怎麼實現低通濾波器模糊影像功能的詳細內容。更多資訊請關注PHP中文網其他相關文章！