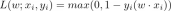清華大學崔鵬：可信賴智慧決策架構及實踐

一、一個可信任智慧決策框架

#首先和大家分享一個可信任智慧決策框架。

1、比預測更重要的決策

在實際的許多場景中，決策比預測更重要。因為預測本身的目的並不是單純地預知未來長什麼樣子，而是希望透過預測去影響當下的一些關鍵行為和決策。

在許多領域，包括商業社會學領域，做決策非常重要，例如持續的業務成長（Continual business growth）、新商業機會發現（New business opportunity）等，如何透過數據驅動來更好地支撐最終的決策，是人工智慧領域不可忽視的一部分工作。

2、無所不在的決策

決策場景無所不在。眾所周知的推薦系統，給一個使用者推薦什麼樣的商品，實際上是在所有商品裡做了一個選擇決策（selection decision）。在電子商務中的定價演算法，例如物流服務定價等，如何為一個服務制定一個合理的價格；在醫療場景中，針對病人的症狀，應該推薦使用哪種藥物或治療方式，這些都是介入性的決策場景。

3、決策的通常做法1：用模擬器做決策

學術界和產業界對決策都不陌生，有一些常用的方法去解決或是探討決策的問題，總結下來有兩種通常的做法。

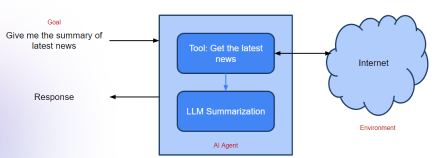
第一種通常做法是用模擬器做決策，也就是強化學習（reinforcement learning）。強化學習是非常強大的一類做決策的方法體系，相當於有一個真實場景（environment），或者有一個對真實場景的模擬，就可以透過智慧代理（agent）不斷和真實場景進行試誤學習，不斷探索關鍵行為（action），最終找到在此真實場景中收益（reward）最大的關鍵行為。

整套強化學習的決策體系在許多實際應用問題上，會被大家先想到。但是在真實的應用場景下，使用強化學習最大的挑戰是有沒有一個很好的對真實場景的模擬器。模擬器的建構本身就是一項極具挑戰性的任務。當然例如阿爾法狗（Alphago）象棋等遊戲場景，整體上來講規則是相對封閉的，去構造一個模擬器還是比較容易的。但是在商業上和真實生活中，大多是開放性的場景，例如無人駕駛，很難給出一個非常完整的模擬器。要構造出模擬器，就需要對該場景有非常深入的理解。因此，建構模擬器本身可能是比做決策、做預測更難的問題，這其實是強化學習的限制。

4、決策的常見做法 2：用預測做決策

另外一種通常做法就是用預測去做決策。指的是，雖然現在不知道什麼樣的決策好，但假如有一個預測器，能夠在預測空間裡邊“打哪指哪”，如下圖左邊所示，像人射箭一樣，可以先放幾箭去打靶子，發現哪一箭射得比較好，就取這一箭的關鍵行為做相關決策。如果有這樣的一個預測空間，就可以用預測來做決策。

但是決策的效果取決於預測空間的準確性，到底預測得準不準。雖然在預測空間，打中了 10 次靶子，但當應用到實際的生活或產品時，中靶次數為 0，這就說明預測空間是不準的。到目前為止在預測任務上，最有信心的一個場景是在獨立同分佈假設下做預測，即測試分佈（test distribution）和訓練分佈（training distribution）是同一個分佈，當下有非常強大的預測模型（prediction model），可以很好地解決實際問題。這告訴我們：預測準確度好不好，某種程度上取決於實際場景下的測試資料和訓練資料的分佈是否滿足獨立同分佈。

繼續深入思考預測準確度問題。假設基於歷史資料 P(X,Y) 建構了一個預測模型，然後去探索一些不同的關鍵行為所帶來收益，即如前面所述的多次射箭，看到底哪一次靶數最大。拆解一下，可以分為兩類不同的情況。

第一類是給定決策變量，最佳化取值。事先知道了輸入變數X 中哪一個是比較好的決策變量，例如價格是X 裡面的決策變量，則變化價格變數的值，用已建構出來的P(X,Y) 預測模型去預測改變取值後的情況如何。

另一類是尋求最優決策變量，並最佳化取值。事先並不知道X 中哪一個是比較好的決策變量，場景上相對比較靈活，需要尋求最優的決策變量並優化其取值，也就是變化最優的決策變量的取值，然後看哪個取值經過預測模型預測的結果好。

基於這樣的前提假設，在改變決策變數的值時，實際上是改變了P(X)，即P(X) 發生了變化，P(X,Y) 肯定會發生變化，那麼獨立同分佈的假設本身就不成立了，意味著預測實際上很有可能失效。因此決策問題，如果用預測的方式來做，就會引發分佈外泛化的問題，因為改變了決策變數的值，一定會發生分佈偏移（distribution shift）。在分佈偏移的情況下，怎麼樣做預測，是屬於分佈外泛化的預測問題範疇，不是今天文章的主題。如果在預測領域能夠解決分佈外泛化的預測問題，用預測做決策也是可行的路徑之一。但當下用 ID（In-Distribution）或直接預測（direct prediction）的方法做決策，從理論上來講是失效的，是有問題的。

#5、決策問題是因果範疇

在談到決策問題時，通常都會直接把決策問題和因果掛鉤，所謂決策，就是要做一個什麼樣的決定，肯定要問為什麼做這樣一個決定，很明顯存在因果鏈條，在學界很多學者的共識是：要解決決策問題，是繞不開因果的，也就是要從可觀測的數據（observational data）上來去獲取足夠的因果關係資訊（causal information），並理解相關的因果機制（causal mechanism ），然後基於因果機制再去設計最終做決策的一些策略。如果能夠把整個過程都理解得很透徹，就能完美地復原整個因果機制，這樣決策就不是問題，因為實際上相當於具有了上帝視角，就不存在做決策的挑戰。

6、一種對決策的框架性描述

#早在2015 年，Jon Kleinberg 就在一篇論文中發表過：決策問題不是只有因果機制能解決，也就是不是所有的決策問題都需要因果機制去解決。 Jon Kleinberg 是康乃爾大學的知名教授，著名的 hits 演算法、六度風格理論等都是 Jon Kleinberg 的研究成果。 Jon Kleinberg 在 2015 年發表了一篇關於決策問題的論文，「Prediction Policy Problems」[1]。他認為有些決策問題就是預測策略問題，為了證明該論點，給出了決策的框架性描述，如下圖所示。

#

Π 是收益函數（Payoff function），x₀ #是決策變數（Decision Variable），Y 是因決策變數產生的結果（Outcome ），Π 其實是 x_#0 和Y 的函數。那 x₀ 怎麼變化，Π 是最大的，就可以去求這樣的一個導數：

然後將它展開為：

展開後，根據Y 和 x_#0 是否不相關，等式右邊分別刻畫了兩種決策（ decision）場景。 第一種決策場景，就是Y 和 x₀ 不相干時，即，但 和Y 是有關係的，這種情況下，如果能夠很好地預測Y，就能用已預測的Y，更有針對性地用  來做決策，這就是預測性決策問題。另外一個決策場景為，x0 做了這樣的一個決策，會影響 Y，Y 又會影響收益，這就是因果決策問題。那什麼情況下決策場景是因果性的，什麼情況下是預測性的呢，後續會有案例解釋；當然也有複合性決策場景，既有因果性的，又有預測性的。到此，初步地框架性地描述了決策問題是怎樣的。

7、決策場景的兩個案例

如上圖所示的兩種決策場景，其中 x₀# 是決策變數（decision variable），在兩個場景下的定義是分別不同的。

先看左邊的場景案例。要不要帶傘，和是否下雨之間是沒有關係的，即 x_#0 和Y 不相關，帶入

在

中，即：

為0，則：

那麼預測是否要下雨，最終的收益是不一樣的。所以這個例子很明顯是一個預測性決策（prediction decision）。

右邊的案例是如果你是酋長，要不要花錢請人跳大神求雨，其實很大程度取決於「跳大神「到底能不能求雨，是否有因果效應。等式右邊的

，如果能預測出來是否下雨，那麼：

#為 0，即收益（是否下雨）和決策變數（跳不跳大神）其實是沒有任何關係的。那麼這就不是一個預測性決策，是一個純粹的因果決策。

透過上述兩個實際的決策案例場景，可以將決策問題分為兩類：預測性決策和因果性決策，並且Jon Kleinberg 給出的決策問題的框架，也很好地說明了決策的劃分。

8、決策的複雜性

# Jon Kleinberg 的論文中給出的一個觀點是，對於預測性決策問題，就只管預測的好不好，因果機制不一定是必須的，預測模型在決策場景上很好用，對決策問題有很好的表達能力，可以把很多情況都融合在一起。但實際上決策的複雜性是超越先前對預測場景的理解的。大部分情況下，在解決預測問題時，只是盡力而為（best effort），盡量用更複雜的模型，更多的數據，希望提升最終的準確率，即盡力而為的模型（best effort model） 。

但決策情境下受限制的限制因素遠比預測要多。決策其實是最後一公里，最後做出的某個決策確實會影響各個面向，影響許多利害關係人，涉及非常複雜的社會性、經濟性的因素。例如，同樣是貸款，對於不同性別、不同區域的人是否有歧視，就是很典型的演算法公平性問題。大數據殺熟，同樣的商品對不同人給予不同的價格，也是一個問題。近年來大家深有體會的資訊繭房，就是不斷按照用戶興趣或相對比較窄的頻譜上的興趣，集中地對某個用戶進行推薦，就會造成資訊繭房。長此以往，就會出現一些不好的文化和社會現象。所以做決策時，要考慮更多的因素，才可以做出可信的決策。

9、一個可信任智慧決策的架構

從決策可信角度對Jon Kleinberg 所給的決策問題架構持續解讀。雖然 Jon Kleinberg 本身提出這個決策問題架構是主張預測模型（prediction model）對於決策問題的有效性，但實際上該決策問題架構的內涵非常豐富，以下依序對此決策問題架構的各項進行解讀。

首先#是最右邊的一項：

針對一些反事實的現象，就是某些 x₀ #沒有出現，但假設它出現，到底Y 會發生一些什麼樣的變化，是典型的反事實推理，是因果推論中核心的部分，當然在Judea Pearl 給出的框架裡，它是第三階梯了。關於反事實推理有很多不同的理解和解釋，這裡所談到的反事實推理姑且認為是合理的。

第二項是，實際上相當於收益函數和模型結果之間的關係。 Y 和 Π 的關係有比較簡單的場景。例如進行商品推薦時，給用戶推薦什麼樣的商品，用戶會點擊，優化後的最後的收益函數（Payoff function），其實就是整體點擊率。這種是兩者關係比較簡單的場景。但是在實際業務中，不管是從平台還是從監管的角度，Y 和 Π 的關係大部分情況下是非常複雜的。例如後續會講到的一個案例，在做平台的收益優化時，不能只看當下的點擊率，要看長期收益；當看長期的收益時，Y 和Π 的關係就會相對複雜，即複雜收益。

#

第三項是Y，核心任務就是做預測（prediction），但如果預測（prediction）是用來做決策的，並且決策場景是社會屬性的，例如影響到個人徵信，影響到高考是不是被錄取，影響到犯人是否會被釋放等，那麼所有的這些所謂的預測性的任務，都會要求預測必須是公平的，不能去用一些比較敏感（sensitive）的維度變量，例如性別、種族、認同等去做預測。

第四項#是：

，指的是收益和決策之間的關係。常規來講，應該是在收益最大化的前提下去做決策。但現實中，不管是國內還是國際上，都逐漸地加大了對平台性演算法的監管力度，即在收益函數（Payoff function）的設計上增加監管因素，使得做決策時是有一定限制的。例如定價，不能平台隨意定，而是在收益函數（Payoff function）裡加入一些監管因素，這就是可監管決策。

這個決策問題框架包含了不同層面的場景，也可以認為它有以上四個不同的子方向。但是整體上以上四個子方向都和可信決策是非常相關的，也就是如果要保證角色可信，必須要考慮方方面面的因素。但整體上來講，都可以用 Jon Kleinberg 所給的框架來進行統一的表述。

接下來會依序介紹可信任智慧決策架構下的四個子方向：反事實推理、複雜效益、預測公平性和可監管決策。

二、可信任智慧決策中的反事實推理

首先介紹關於可信智能決策架構下的反事實推理的一些思考與實踐。

1、反事實推理

反事實推理有三個場景。

第一是策略平均效果評估（Off-Policy Evaluation)。對於一個給定的策略（policy），不希望進行AB 測試，因為AB 測試成本太高，因此在離線資料上評測該策略上線後，會有什麼樣的效果，就相當於對整個族群（population）或所有sample 進行評測，例如對所有使用者群體的一個整體效果評估。

第二是策略個體效果評估（Counterfactual Prediction），是對策略在一個個體層面的效果進行預測，不是整體平台性策略，而是針對某個個體進行一定的干預後，會有什麼樣的效果。

第三是策略最佳化（Policy Optimization），即怎麼麼樣去為一個個體選擇效果最好的介入。和個別效果預測不一樣，個別效果預測是先知道怎麼幹預，然後預測幹預後的效果；策略優化是事先不知道怎麼幹預，但尋求怎樣幹預之後的效果最好。

2、策略平均效果評估

#（1） 策略平均效果評估的問題框架概述

##策略平均效果評估，就是基於從策略Π₀（Behavior policy ）產生的離線資料D，評估策略Π（Target policy）的效用值（Utility）。

#

Π₀ 是現有的策略，例如現有推薦系統中一直在使用的建議策略。

現有策略下產生的離線資料D 蘊含至少三個維度，如上圖所示，x _i 就是背景資訊（Context），例如在推薦系統中的使用者和商品的屬性；a_i 是行為， 例如推薦系統中某個商品有沒有對使用者曝光；r_i 是最終結果（reward），例如推薦系統中使用者是否最終點擊或購買商品。

基於歷史資料去評測一個新的策略 Π（Target policy）的效用值（Utility）。所以整體的框架就是在某個背景（context）下，某策略（policy）會有對應的行為或是乾預變數（treatment），這個介入變數（treatment）觸發後，就會產生對應結果。其中，效用值（Utility）即前述的收益（Payoff），在簡化 前提下，效用值就是所有使用者產生的結果的總和，或平均效果。

（2）策略平均效果評估的現有方法

#傳統的策略平均效果評估方法是基於結果預測的方法（Direct Method），在新的策略（policy）下給定 xi，對於主體，建議曝光還是不曝光，即對應的行為，就要預測如果進行了曝光，最終用戶會不會購買，或會不會點擊，也就是最終獲得的結果（reward）。但請注意，reward 實際上是預測函數（prediction function），是透過歷史資料得到的。歷史資料中的x、a 和r 的聯合分佈（joint distribution）實際上是在 Π0 下產生的，現在換了一個Π 所產生的資料分佈，再用原來 Π0 下產生的聯合分佈預測模型（joint distribution prediction model）去做預測，很顯然這是一個OOD（Out-of-Distribution）問題，如果後面用OOD 預測模型，那麼資料分佈偏移問題有可能得到緩解，如果用一個ID（In-Distribution）預測模型，原則上一定會出問題。這是傳統的策略平均效果評估方法。

另外一種方法是基於因果推斷的，引入了傾向指數（propensity score），其核心思想是，用原始策略下的三元組（xi，ai，ri ) 在新的策略下，到底應該使用什麼樣的權重來加權最終產生的結果。權重應該是給定 xi，在新策略下 xi 曝光（ai）的機率和在原有策略下 xi 進行曝光（ai）的機率之比，即在新的策略下，對一個三元組所對應的結果進行加權的一個係數。此種做法最難的地方是在原始策略下，給定 xi 後，對應 ai 的機率分佈其實是不知道的，因為原始策略可能很複雜，也有可能是多個策略的疊加，並沒有辦法顯性地刻畫對應的分佈，因此需要進行估算，那麼就會存在估算是否準確的問題，並且該估算值在分母上，會導致整個方法的分佈方差（variance）非常大。另外使用傾向指數（propensity score）的估計本身就存在問題，假設傾向指數（propensity score）的函數是線性的，還是非線性的，是什麼形式，估計是否準確等等。

（3）策略平均效果評估的新方法：FCB estimator

借鑒因果關係（Causality）的直接混淆變數平衡（directly confounder balancing），提出了對樣本直接加權的方法，使得加權後，可以保證在各個對應行為群（action group）的分佈P(X|a_i）整體上和P(X) 是一致的。

#

歷史資料是在給定Π₀ 的情況下產生的，要去掉因Π_#0 所造成的分佈偏差（bias），具體做法如上圖所示，原始的資料分佈P(X)，在Π₀ 的作用下，相當於把P( X) 分為若干個子分佈P(X|a=1)、P(X|a=2)、P(X|a=3)、...、P(X|a=K)，即不同的行為下對應P(X) 的子集，是無偏的分佈，每個行為群下都有因Π₀ 而造成的偏差，要去掉偏差，可以透過對經Π₀ 而產生的歷史資料進行重加權，使得加權以後的所有子分佈，都逼近原始分佈P(X)，即樣本直接加權。

預測一個新的策略在歷史資料的前提下最終的效果會是什麼樣的，需要分兩步驟進行。第一步，就是如前所述，先透過樣本直接加權的方式去掉原始策略 Π₀ 所帶來的偏差。第二步，要預測新策略Π 的效果，也就是新策略Π 所造成的偏差下去預估最終的效果，所以需要加上新策略Π 造成的偏差 

因此：

#其中 w_i 就等於第一步去掉 Π₀ ##帶來的偏差：

# 相當於把新策略的偏差加上，這樣就可以預測一個新的策略最終的效果。具體方法不贅述，可以參考論文 [2]。

#新方法FCB Estimator 最後的提升效果如上圖所示，提升效果非常明顯，不管是從偏差（bias），還是RMSE 的維度來講，相對提升大概有15%-20%。 FCB Estimator 在變化 sample size 和 context 維度的不同場景下都顯著優於 baseline。相關論文發表在 KDD 2019 [2]。

3、策略個體效果預測

（1）策略個體效果預測的整體描述

#策略個體效果預測就是要充分考慮個體異質性，直接對個體實施差別化干預，即尊重個體意志，對不同的個體實施不同的干預。

（2）現有方法的限制

策略個體效果預測常用的方法是直接對個體進行預測建模，也就是基於歷史觀測資料：

然後訓練得到反事實預測模型：

，即給定了 X 和 T，能比較合理和準確地預測實際效果 y 是怎樣的。

#如果直接在歷史資料分佈下，做迴歸分析或類似的模型，是有問題的。因為歷史觀測資料中的 t_i 與 x_i 並不獨立，直接學習（X，T）與Y 直接的映射函數必然受到X 與T 之間的關係影響，也就相當於給定了一個 x_i，在歷史資料裡面必然對應一個 t# #i_，例如 ti _{就應該等於0，當幹預T 時，例如硬要把} ti _{改成1，實際上就已經不服從原來的歷史分佈了，意味著在歷史資料分佈下構造出來的ID（In-Distribution）預測模型就無效了，觸發了OOD（Out-of-Distribution）。}

因此在建構所謂的預測模型時，就需要消除X 和T 之間的關聯，分別估計X 對Y 的影響和T 對Y 的影響，這種情況，如果幹預或改變了T，和X 就沒關係，到底對Y 會有什麼影響和變化，完全由T->Y 這條鏈路決定，就不存在OOD（Out-of- Distribution）問題了。

#傳統做法#是採用樣本重加權（Sample Re- weighting）的方法來去除X 和T 之間的關聯，有兩種方法：（1）逆傾向性分數加權，（2）變數平衡。但這些方法都存在局限性：只適用於簡單類型的干預變數（treatment）場景，二值或離散值。在真實的應用場景下，例如推薦系統，幹預變數（treatment）維度很高，給使用者推薦商品，推薦的是一個束（bundle），即從很多商品中進行推薦。當介入變數（treatment）維度很高時，使用傳統的方法，把初始介入變數（raw treatment）和混淆變數（confounder） X 直接去關聯，複雜度非常高，甚至樣本空間不夠來支撐高維度的介入變數（treatment）。

（3）策略個體效果預測新方法：VSR

如果假設高維度的干預變數（treatment）存在低維隱變數結構，也就是給出高維度的干預變數（treatment）原則上不是隨機出來的，例如推薦系統中，給定推薦策略推薦出來的商品束（bundle），裡面的商品和商品之間都有各種各樣的關係，存在低維隱變數結構，也就是推薦商品清單由若干因素決定。

如果高維度的干預變數（treatment）下有一個隱變數（latent variable） z，實際上可以把問題轉換為x 與z 之間的去關聯，即和隱性因素（latent factor）之間去相關。透過這種方式，可以在有限的樣本空間下實現束處理（bundle treatment）。 #

因此提出了新方法 VSR。 VSR 方法中，首先是高維度幹預變數（treatment）的隱變數z（latent variable z）的學習，即使用變分自編碼器（VAE）進行學習；然後是權重函數w（ x，z）的學習，透過樣本重加權的方式對x 和z 之間進行去相關（decorrelation）；最後在重加權的相關分佈下直接使用迴歸分析模型（regression model），就能得到一個比較理想的策略個體效果預測模型。

#上圖是新方法VSR 的實驗驗證，是在一些場景下，透過Recsim 模擬器產生部分數據，以及部分人工模擬的數據，進行驗證。可以看到，在不同的 p 的值下，VSR 的性能都相對比較穩定，相比其他方法有了很大的提升。相關論文發表在 NeurIPS 2020 [3]。

4、策略最佳化

#策略優化和前面兩種的預測評估是有本質差異的。預測評估都是提前給定一個策略（policy）或個人化的介入（individual treatment），去預估最終的結果。策略優化，也叫策略學習，目標只有一個結果變大。例如收益要成長，應該施加什麼樣的介入。

#如果現在有一個反事實的個體層級的預測模型f，即策略個體效果預測模型f，也就是給定 x_i 和 t_i，就可以估計出來對應的結果，那麼就可以對T 進行遍歷，t 取什麼值時，f 的值最大。就相當於建構一個比較好的預測空間，在預測空間中「打哪指哪」。

但把策略最佳化問題退化為策略個體效果預測模型的構建，是有問題的。策略個體效果預測的目標，如前所述，實際上是相當於給定了一個幹預，希望反事實預測出來的情況與真實情況的誤差盡量比較小，並且對於所有給定的干預，都希望比較準確。策略最佳化的目標，是找到的 p^#f 點離真實狀況上帝視角下的最優決策的結果之間的距離越小越好，並不是一個全空間的策略個體效果預測的問題，而是能不能找到離最優點比較近的區域，以及能不能準確地預測最優點。策略優化和策略個體效果預測在目標上是不一樣的，有明顯的差異。

#如上圖的案例圖所示，橫軸是不同的介入（treatment ），綠線是上帝視角下的真實函數，反映某個幹預下真實的結果；紅線和藍線反映的兩個預測模型下的結果。從策略個體效果預測的評估角度來看，很明顯藍線是優於紅線的，藍線離綠線的整體偏差，遠小於紅線離綠線的整體偏差。但從最優決策的角度來看，紅線的最優結果和上帝視角的綠線的最優結果更接近，相應的干預也更接近，而藍線的明顯要更遠。因此一個更好地策略個體效果預測模型，不一定能夠得到一個最優的決策；並且在真實的場景下，數據量通常是不充分的，在全空間下去做優化，還是從結果的角度僅在一個子區域裡做優化，優化的效果和力道是不一樣的。

#

因此提出了策#略優化的新方法 OOSR，目的是加強結果較好的介入區域的預測力度和優化力度，而不是在全空間去做優化。因此在做優化時，在做面向結果的加權（outcome-oriented weighting）時，當前的干預離給定的已經訓練下的最優解的距離越近，則優化力度更大# 。

#上圖是OOSR 的實驗驗證，可以看出，從各個角度上提升都非常明顯，有幾倍的提升，而且變化了selection bias 的強度後，效果也依舊非常好。相關論文發表在 ICML 2022 [4]。

5、反事實推理總結

# #不管是做策略評估，還是策略優化、策略個體效果預測，實際上都是在利用因果關係（Causality），來對決策了解更多，讓決策表現更好，或者讓決策變得更加個性化。當然針對不同的場景，還有很多開放性的問題。

三、可信任智慧決策中的複雜效益

##在研究複雜效益，即：

#時，考慮這樣一個場景，例如推薦系統，希望推薦的商品或資訊等用戶都會購買或點擊，同時也會實施一些刺激，例如降價，或進行紅包回饋等等，有很多類似的商業運營策略，雖然短期內銷量提高了，提升效果很顯著，但從長期看並沒有非常顯著的變化，也就是商業上的很多刺激，並不是把不想買的變成想買的，而是本來一個月總需求量是4 件，這次降價就一次性把4 件都買完了。因此在做模型最佳化時，不能只考慮短期收益，兼顧短期收益和長期收益，共同去優化策略。

##################################要想兼顧短期和長期收益，共同優化策略，有兩個非常重要的面向。第一，要對消費者的選擇模式有比較深入的理解。當給定一個使用者時，是沒有辦法得到真實的消費者選擇模型的，需要透過研究和挖掘的方式不斷地探索，一個是探索消費者選擇模型，另一個就是探索在消費者選擇模型下怎麼樣最大化長期收益和短期收益，以及兩者的平衡。在這方面的工作如上兩張圖所示，就不展開講了。 #########################

从最后的效果上来看，如上图所示，在很多真实场景都有显著的收益提升。相关论文发表在 NeurIPS 2022 [5]。

四、可信智能决策中的预测公平性

如果预测要参与到决策中，特别是面向社会性的决策，一定要兼顾预测的公平性。

关于公平性，传统的做法有 DP 和 EO，要求男女的接受概率是相等的，或者对于男女的预测能力是一样的，都是比较经典的指标。但 DP 和 EO 并不能从本质上解决公平性的问题。

比如在大学录取的案例中，理论上各个系男生和女生的录取率应该都是一样的，但实际总体上会发现女生的录取率偏低，实际上这是一种辛普森悖论。大学录取本质上是一个公平的案例，但是 DP 的指标检测出来，会认为不公平，实际上 DP 并不是一个非常完美的公平性指标。

EO 模型本质上确实是性别参与了决策，但在一个不公平的场景下，如果对于男性和女性都有一个完美预测因子，就认为是公平的。这就说明 EO 的鉴别率是不够的。

2020 年提出了有条件的公平性（conditional fairness）这一概念。有条件的公平性并不是要绝对地去保证最终结果和敏感因素（sensitive attributes）独立，而是给定某些公平性变量（fair variable），最终结果和敏感因素独立，就认为是公平的。比如专业选择，是公平的，是一个 fair variable，因为是学生主观能动性可以决定的，不存在公平性问题。

这样做带来了非常多的好处。从预测的角度来讲，公平性和预测之间实际上就是一种权衡，也就是公平性要求越强，可用的预测变量（predictive variable）就会越少。比如在 EO 的框架下，只要一个变量是在从性别到结果决策之间的链路上，是都不能用的，用了就会导致很多变量实际上预测效率非常高，但是不能做预测。但在有条件公平性下，给定了一个公平性变量，不管是不是在链路上，都可以保证预测效率可用。

在此框架下，设计和提出了 DCFR 算法模型，如下三图所示。

下圖 DCFR 演算法的實驗驗證。從整體來看，DCFR 演算法能夠取得更好的預測和公平性的折中，從帕雷托最優的角度來講，左上的曲線實際上是更優的。相關論文發表在 KDD 2020 [6]。

##最後是可信任智慧決策中的可監管決策。

#現在的平台有很多個人化定價機制。本質上來講，個人化定價是可以最大化社會的總效率和總剩餘的。但是在某一些極端情況下，商家會把所有的剩餘都拿走，而不給用戶留一分的剩餘，這是我們不希望看到的。

##從總體上看，就是要設計出一種策略，可以使得在社會總剩餘不受太大影響的情況，商家讓渡一部分可視為財富的剩餘給消費者。

最終設計出了一種調控手段來解決這個問題，如下圖。也就是例如同一個商品，最高價和最低價之間不能超過一個 ，或不能超過一定的比例。理論上可以證明這樣設計的規則可以實現如前所述的最佳化目標。

#################################################################在此種場景下，本質上是透過對收益函數增加一些約束，使得在做決策的時候必須有另一個層面的考慮。因此在這個體系下，可以把監管相關的一些策略或工具加入進來。 ##############################六、可信任智慧決策的摘要############################################################# ##################以上就是在可信智能決策的這樣一個框架下，在反事實推理、複雜收益、預測公平性和可監管決策各個單點上做的一些嘗試。整體而言，決策的想像空間遠比預測更大。在決策的領域裡，還有很多和我們生活、商業息息相關的開放性問題值得探究。相關論文發表在WWW 2022 [7]。 ##########

PS: 本文涉及的許多技術細節，可以參考崔鵬老師團隊近期在可信智慧決策方向上所發表的論文。

七、參考文獻

#[1] Jon Kleinberg, Jens Ludwig, Sendhil Mullainathan, Ziad Obermeyer. Prediction Policy Problems. AER, 2015。

[2] Hao Zou, Kun Kuang, Boqi Chen, Peng Cui, Peixuan Chen. Focused Context Balancing for Robust Offline Policy Evaluation. KDD, 2019。

[3] Hao Zou, Peng Cui, Bo Li, Zheyan Shen, Jianxin Ma, Hongxia Yang, Yue He. Counterfactual Prediction for Bundle Treatments. NeurIPS, 2020。

[4] Hao Zou, Bo Li, Jiangang Han, Shuiping Chen, Xuetao Ding, Peng Cui. Counterfactual Prediction for Outcome-oriented Treatments. ICML, 2022 。

[5] Renzhe Xu, Xingxuan Zhang, Bo Li, Yafeng Zhang, Xiaolong Chen, Peng Cui. Product Ranking for Revenue Maximization with Multiple Purchases. NeurIPS, 2022。

[6] Renzhe Xu, Peng Cui, Kun Kuang, Bo Li, Linjun Zhou, Zheyan Shen and Wei Cui. Algorithmic Decision Making with Conditional Fairness. KDD , 2020。

[7] Renzhe Xu, Xingxuan Zhang, Peng Cui, Bo Li, Zheyan Shen, Jiazheng Xu. Regulatory Instruments for Fair Personalized Pricing. WWW, 2022。

#

以上是清華大學崔鵬：可信賴智慧決策架構及實踐的詳細內容。更多資訊請關注PHP中文網其他相關文章！