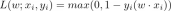一、DNN泛化能力的問題
論文主要探討的是, 為什麼過參數的神經網路模型還能有不錯的泛化性?即不是簡單記憶訓練集,而是從訓練集中總結出一個通用的規律,從而可以適配於測試集(泛化能力)。

以經典的決策樹模型為例, 當樹模型學習資料集的通用規律時:一種好的情況,假如樹第一個分裂節點時,剛好就可以很好區分開不同標籤的樣本,深度很小,相應的各葉子上面的樣本數是夠的(即統計規律的數據量的依據也是比較多的),那這會得到的規律就更有可能泛化到其他數據。 (即:擬合良好, 有泛化能力)。

另外一種較差的情況,如果樹學習不好一些通用的規律,為了學習這個資料集,那樹就會越來越深,可能每個葉子節點分別對應著少數樣本(少數據帶來統計資料可能只是雜訊),最後,死記硬背地記住所有資料(即:過擬合無泛化能力)。我們可以看到過深(depth)的樹模型很容易過度擬合。
那麼過參數化的神經網路如何達到良好的泛化性呢?
二、 DNN泛化能力的原因
本文是從一個簡單通用的角度解釋-在神經網路的梯度下降優化過程上,探討泛化能力的原因:
我們總結了梯度相干理論:來自不同樣本的梯度產生相干性,是神經網路能有良好的泛化能力原因。當不同樣本的梯度在訓練過程中對齊良好,即當它們相干時,梯度下降是穩定的,可以很快收斂,並且由此產生的模型可以有良好的泛化性。否則,如果樣本太少或訓練時間過長,可能無法泛化。

基於這個理論,我們可以做出以下解釋。
2.1 寬度神經網路的泛化性
更寬的神經網路模型具有良好的泛化能力。這是因為,更寬的網絡都有更多的子網絡,對比小網絡更有產生梯度相干的可能,從而有更好的泛化性。換句話說,梯度下降是優先考慮泛化(相干性)梯度的特徵選擇器,更廣泛的網路可能僅僅因為它們有更多的特徵而具有更好的特徵。
- 論文原文:Generalization and width. Neyshabur et al. [2018b] found that wider networks generalize better. Can we now explain this? networks generalize better. Can we now explain this? veloping works, worksive works 及 so the sub-network with maximum coherence in a wider network may be more coherent than its counterpart in a thinner network, and hence generalize better. In other words, since—as cussed indient 10—grased as discussed indient 10— well-generalizing (coherent) features, wider networks are likely to have better features simply because they 順ave features simply because they 0have features simply because Lottery Ticket Hypothesis [Frankle and Carbin, 2018]
- 論文連結:https ://github.com/aialgorithm/Blog
但是個人覺得,這還是要區分下網路輸入層/隱藏層的寬度。特別是資料探勘任務的輸入層,由於輸入特徵是通常是人工設計的,需要考慮下做下特徵選擇(即減少輸入層寬度),不然直接輸入特徵噪音,對於梯度相干性影響不也是有乾擾的。
2.2 深度神經網路的泛化性
越深的網絡,梯度相干現像被放大,有更好的泛化能力。

在深度模型中,由於層之間的回饋加強了有相干性的梯度,因此存在相干性梯度的特徵(W6)和非相干梯度的特徵( W1)之間的相對差異在訓練過程中呈指數放大。從而使得更深的網路更偏好相干梯度,從而更好地泛化能力。
2.3 早停(early-stopping)
透過早停我們可以減少非相干梯度的過度影響,提高泛化性。
在訓練的時候,有些容易樣本比其他樣本(困難樣本)更早擬合。訓練前期,這些容易樣本的相干梯度做主導,並且很容易擬合。訓練後期,以困難樣本的非相干梯度主導了平均梯度g(wt),從而導致泛化能力變差,這個時候就需要早停。

- (註:簡單的樣本,是那些在資料集裡面有很多梯度共同點的樣本,正由於這個原因,大多數梯度對它有益,收斂也比較快。)
2.4 全梯度下降VS 學習率
我們發現全梯度下降也可以有很好的泛化能力。此外,仔細的實驗顯示隨機梯度下降並不一定有更優的泛化,但這並不排除隨機梯度更容易跳出局部最小值、起正則化等的可能性。
- Based on our theory, finite learning rate, and mini-batch stochasticity are not necessary for generalization
#我們認為較低的學習率可能無法降低泛化誤差,因為較低的學習率意味著更多的迭代次數(與早停相反)。
- Assuming a small enough learning rate, as training progresses, the generalization gap cannot 我 training: with 40 more steps, stability can only degrade. If this is violated in a practical setting, it would point to an interesting limitation of the theory
2.5 L2、L1正規化
目標函數加入L2、L1正則化,對應的梯度計算, L1正規項需增加的梯度為sign(w) ,L2梯度為w。以L2正規為例,對應的梯度W(i 1)更新公式為:圖片

我們可以把「L2正則化(權重衰減)」看成是一種“背景力”,可將每個參數推近於資料無關的零值( L1容易得到稀疏解,L2容易得到趨近0的平滑解) ,來消除在弱梯度方向上影響。只有在相干梯度方向的情況下,參數才比較能脫離“背景力”,並基於數據完成梯度更新。

2.6 梯度下降演算法的進階
- #Momentum 、Adam等梯度下降演算法
Momentum 、Adam等梯度下降演算法,其參數W更新方向不僅由目前的梯度決定,也與先前累積的梯度方向有關(即,保留累積的相干梯度的作用)。這使得參數中那些梯度方向變化不大的維度可以加速更新,並減少梯度方向變化較大的維度上的更新幅度,由此產生了加速收斂和減小震盪的效果。
- 抑制弱梯度方向的梯度下降
我們可以透過最佳化批次梯度下降演算法,來抑制弱梯度方向的梯度更新,進一步提高了泛化能力。例如,我們可以使用梯度截斷(winsorized gradient descent),排除梯度異常值後的再取平均值。或取梯度的中位數代替平均值,以減少梯度異常值的影響。
小結
文末說兩句,對於深度學習的理論,有興趣可以看下論文提及的相關研究。
以上是一文淺談深度學習泛化能力的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM
優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM介紹 恭喜!您經營一家成功的業務。通過您的網頁,社交媒體活動,網絡研討會,會議,免費資源和其他來源,您每天收集5000個電子郵件ID。下一個明顯的步驟是
 Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM
Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM介紹 在當今快節奏的軟件開發環境中,確保最佳應用程序性能至關重要。監視實時指標,例如響應時間,錯誤率和資源利用率可以幫助MAIN
 Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM“您有幾個用戶?”他扮演。 阿爾特曼回答說:“我認為我們上次說的是每週5億個活躍者,而且它正在迅速增長。” “你告訴我,就像在短短幾週內翻了一番,”安德森繼續說道。 “我說那個私人
 pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介紹 Mistral發布了其第一個多模式模型,即Pixtral-12b-2409。該模型建立在Mistral的120億參數Nemo 12B之上。是什麼設置了該模型?現在可以拍攝圖像和Tex
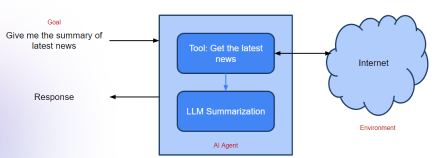 生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想像一下,擁有一個由AI驅動的助手,不僅可以響應您的查詢,還可以自主收集信息,執行任務甚至處理多種類型的數據(TEXT,圖像和代碼)。聽起來有未來派?在這個a


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

SublimeText3 Linux新版
SublimeText3 Linux最新版

Dreamweaver Mac版
視覺化網頁開發工具

禪工作室 13.0.1
強大的PHP整合開發環境

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

VSCode Windows 64位元 下載
微軟推出的免費、功能強大的一款IDE編輯器