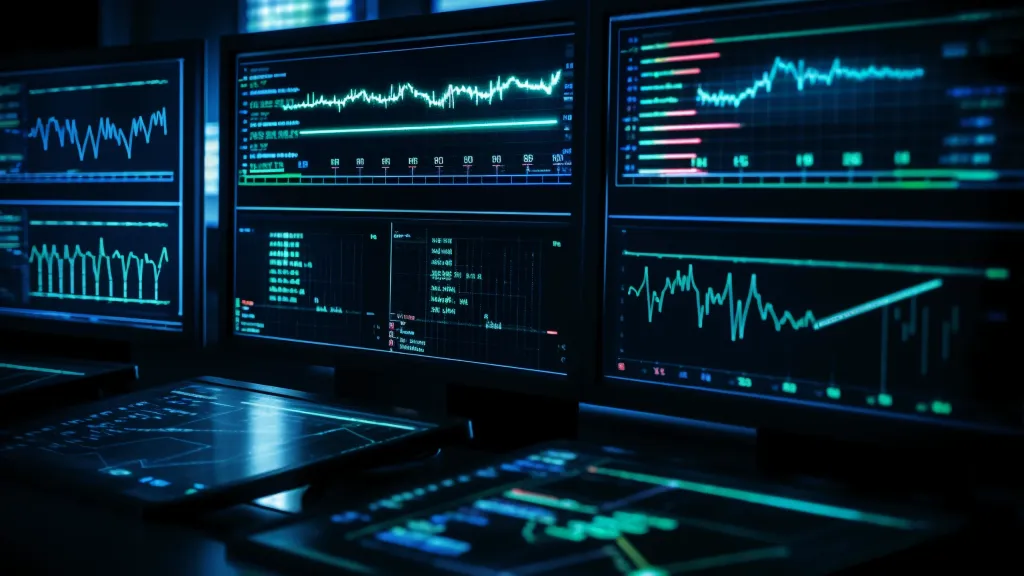
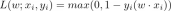譯者| 趙青窕
審校| 孫淑娟
前言
在機器學習中,分類有兩個階段,分別是學習階段和預測階段。在學習階段,基於給定的訓練資料建立模型;在預測階段,該模型用於預測給定資料的反應。決策樹是最容易理解和解釋的分類演算法之一。
在機器學習中,分類有兩個階段,分別是學習階段和預測階段。在學習階段,基於給定的訓練資料建立模型;在預測階段,該模型用於預測給定資料的反應。決策樹是最容易理解和解釋的分類演算法之一。
決策樹演算法
決策樹演算法屬於監督學習演算法中的一種。與其他監督學習演算法不同,決策樹演算法可以用於解決迴歸和分類問題。
使用決策樹的目的是創建一個訓練模型,透過學習從先前的資料(訓練資料)推斷出的簡單決策規則來預測目標變數的類別或值。
在決策樹中,我們從樹的根開始來預測一個記錄的類別標籤。我們將根屬性的值與記錄的屬性進行比較,在比較的基礎上,我們跟隨該值對應的分支並跳到下一個節點。
決策樹的類型
基於我們所擁有的目標變數的類型,我們可以把樹分成兩種類型:
#1.分類變數決策樹:有一個分類目標變數的決策樹,稱為分類變數決策樹。
2.連續變數決策樹:決策樹的目標變數是連續的,因此稱為連續變數決策樹。
範例:假設我們有一個預測客戶是否會向保險公司支付續約保費的問題。這裡客戶的收入是一個重要的變量,但保險公司沒有所有客戶的收入細節。現在,我們知道這是一個重要的變量,然後我們可以建立一個決策樹,基於職業,產品和其他各種變數來預測客戶的收入。在這種情況下,我們預測目標變數是連續的。
與決策樹相關的重要術語
1.根節點(root node):它代表整個成員或樣本,這些成員或樣本會進一步被分成兩個或多個同類型的集合。
2.分離Splitting):將一個節點分割為兩個或多個子節點的過程。
3.決策節點(Decision Node):當一個子節點分裂成更多的子節點時,它稱為決策節點。
4.葉子/終端節點(Leaf / Terminal Node):不可拆分的節點稱為葉子或終端節點。
5.修剪(Pruning):我們刪除一個決策節點的子節點的過程稱為修剪。也可以把修建看成是分離的反過程。
6.分支/子樹(Branch / Sub-Tree):整個樹的一個子部分稱為分支或子樹。
7.父節點與子節點(Parent and Child Node):節點可以拆分出子節點的節點稱為父節點,子節點是父節點的子節點。

決策樹透過從根到葉/終端節點的降序方式來對樣本進行分類,葉/終端節點提供樣本的分類方式。樹中的每個節點都充當某個屬性的測試案例,從節點的每個降序方向都對應測試案例的可能答案。這個過程本質上是遞歸的過程,並且對每個在新節點上紮根的子樹採取相同的處理方式。
建立決策樹時所進行的假設
以下是我們在使用決策樹時所做的一些假設:
●首先,將整個訓練集作為根。
●特徵值最好是可以分類的。如果這些值是連續的,那麼在建立模型之前可以對它們進行離散化處理。
●記錄是基於屬性值遞歸分佈的。
●透過使用一些統計方法來把對應屬性依序放置在樹的根節點或樹的內部節點。
決策樹遵循乘積和表達形式。乘積和(SOP)也稱為析取範式。對於一個類,從樹根到具有相同類的葉節點的每個分支都是值的合取,在該類中結束的不同分支構成了析取。
決策樹實作過程中的主要挑戰是確定根節點及每一層節點的屬性,這個問題就是屬性選擇問題。目前有不同的屬性選擇方法來選擇每一級節點的屬性。
決策樹是如何運作的?
決策的分離特性嚴重影響樹的準確性,分類樹和迴歸樹的決策標準不同。
決策樹使用多種演算法來決定將一個節點分成兩個或多個子節點。子節點的創建增加了子節點的同質性。換句話說,相對於目標變數來說,節點的純度增加了。決策樹將所有可用變數上的節點分離,然後選擇可以產生許多同構子節點的節點進行拆分。
演算法是基於目標變數的類型進行選擇的。接下來,讓我們來看看決策樹中會使用到的一些演算法:
ID3→(D3的延伸)
C4.5→(ID3的繼承者)
CART→(分類與回歸樹)
CHAID→(卡方自動交互檢測(Chi-square automatic interaction detection)在計算分類樹時進行多層分離)
#MARS →(多元自適應迴歸樣條)
ID3演算法使用自頂向下的貪婪搜尋方法,在不回溯的情況下,透過可能的分支空間建立決策樹。貪婪演算法,顧名思義,總是某個時刻做出似乎是最好的選擇。
ID3演算法步驟:
1.它以原始集合S作為根節點。
2.在演算法的每次迭代過程中,對集合S中未使用的屬性進行迭代,計算該屬性的熵(H)和資訊增益(IG)。
3.然後選擇熵最小或資訊增益最大的屬性。
4.緊接著用所選的屬性分離集合S以產生資料的子集。
5.演算法繼續在每個子集上迭代,每次迭代時只考慮以前從未選擇過的屬性。
屬性選擇方法
如果資料集包含N個屬性,那麼決定將哪個屬性放在根節點或放在樹的不同層級作為內部節點是一個複雜的步驟。透過隨機選擇任意節點作為根結點並不能解決問題。如果我們採用隨機的方法,可能會得到比較糟糕的結果。
為了解決這個屬性選擇問題,研究人員設計了一些解決方案。他們建議使用以下標準:
- 熵
- 資訊增益
- 基尼指數
- 增益率
- 變異數削減
- 卡方
使用這些標準計算每個屬性的值,然後對這些值進行排序,並將屬性按照順序放置在樹中,也就是說,高值的屬性放置在根位置。
在使用資訊增益作為標準時,我們假設屬性是分類的,而對於基尼指數,我們假設屬性是連續的。
1. 熵
熵是對被處理資訊的隨機性的量測。熵值越高,就越難從資訊中得出任何結論。拋硬幣就是提供隨機資訊的行為的一個例子。

由上圖可知,當機率為0或1時,熵H(X)為零。當機率為0.5時,熵是最大的,因為它在資料中投射出完全的隨機性。
ID3所遵循的規則是:一個熵為0的分支是葉節點,一個熵大於0的分支需要進一步分離。
單一屬性的數學熵表示如下:

其中S表示目前狀態,Pi表示狀態S中事件i的機率或狀態S節點中i類的百分比。
多個屬性的數學熵表示如下:

其中T表示目前狀態,X表示選定屬性
2.訊息增益
資訊增益(Information gain, IG)是一種統計屬性,用來衡量給定屬性根據目標類別分離訓練的效果。建構決策樹就是尋找一個傳回最高資訊增益和最小熵的屬性的過程。

資訊的增加就是熵的減少。它根據給定的屬性值計算資料集分離前的熵差和分離後的平均熵差。 ID3決策樹演算法使用的就是資訊增益的方法。
IG在數學上表示如下:

用更簡單的方法,我們可以得到這樣的結論:

#其中before為拆分前的資料集,K為拆分所產生的子集數量,(j, after)為拆分後的子集j。
3.基尼指數
您可以將基尼指數理解為用於評估資料集中分離的成本函數。它的計算方法是用1減去每個類別的機率平方和。它傾向於較大的分區並且易於實現的情形,而資訊增益則傾向於具有不同值的較小分區的情況。

基尼指數離不開分類目標變數「成功」或「失敗」。它只執行二進制分離。基尼係數越高,不平等程度越高,異質性越強。
計算基尼指數分離的步驟如下:
- #計算子節點的基尼係數,使用上面的成功(p)和失敗(q)的公式(p² q²)。
- 使用分離的每個節點的加權基尼得分計算分離的基尼係數指數。
CART(Classification and Regression Tree)就是使用基尼指數方法來建立分離點。
4.增益率
資訊增益傾向於選擇具有大量值的屬性作為根節點。這意味著它更喜歡具有大量不同值的屬性。
C4.5是ID3的改進方法,它使用增益比,這是資訊增益的修正,以減少其偏置,通常是最好的選擇方法。增益率克服了資訊增益的問題,在進行拆分之前考慮了分支的數量。它透過考慮分離的內在資訊來修正訊息增益。
假如我們有一個資料集,其中包含使用者和他們的電影類型偏好,這些偏好基於性別、年齡組、等級等變數。在資訊增益的幫助下,你將在「性別」中進行分離(假設它擁有最高的資訊增益),現在變數「年齡組」和「評級」可能同樣重要,在增益比的幫助下,我們可以選擇在下一層中進行分離的屬性。

其中before為分離前的資料集,K為分離所產生的子集數量,(j, after)為分離後的子集j。
5.方差削減
方差削減是一種用於連續目標變數(迴歸問題)的演算法。此演算法使用標準方差公式來選擇最佳分離方式。選擇方差較低的分離作為分離總體的標準:

#是平均值,X是實際值,n是值的數量。
計算變異數的步驟:
- #計算每個節點的變異數。
- 計算每一次分離的變異數並作為每個節點變異數的加權平均數。
6.卡方
CHAID是Chi-squared Automatic Interaction Detector的縮寫。這是比較老的樹的分類方法之一。找出子節點與父節點之間的差異具有統計意義。我們透過對目標變數的觀測頻率和期望頻率之間的標準化差的平方和來衡量它。
它與分類目標變數「成功」或「失敗」一起工作。它可以執行兩次或多次分離。卡方值越高,子節點與父節點之間的差異統計意義越高。它產生一個名為CHAID的樹。
在數學上,Chi-squared表示為:

計算卡方的步驟如下:
- 透過計算成功和失敗的偏差來計算單一節點的卡方
- 使用分離的各節點的成功和失敗的所有卡方總和計算分離的卡方
如何避免/對抗決策樹的過擬合(Overfitting)?
決策樹存在一個常見問題,特別是對於一個滿列的樹。有時它看起來像是樹記住了訓練資料集。如果一個決策樹沒有限制,它會給你100%的訓練資料集的準確性,因為在最糟糕的情況下,它最終會為每個觀察產生一個葉子。因此,當預測不屬於訓練集的樣本時,這就會影響準確性。
在此我介紹兩種方法來消除過擬合,分別是修剪決策樹和隨機森林。
1.修剪決策樹
分離過程會產生完全長成的樹,直到達到停止標準。但是,成熟的樹很可能會過度擬合數據,導致對未見數據的準確性較差。

在修剪中,你剪掉樹的分支,也就是說,刪除從葉子節點開始的決策節點,這樣整體的準確性就不會受到干擾。這是透過將實際的訓練集分離為兩個集:訓練資料集D和驗證資料集V,用分離的訓練資料集D準備決策樹,然後繼續對樹進行相應的修剪,以優化驗證資料集V的精度。

在上圖中,樹左側的「Age」屬性已經被修剪,因為它在樹的右側更重要,因此消除了過擬合。
2.隨機森林
隨機森林是整合學習(Ensemble Learning)的一個例子,我們結合多種機器學習演算法來獲得更好的預測效能。因為建構樹時訓練資料集是隨機抽樣的,分離節點時會考慮特徵的隨機子集,所以我們把這種方法稱為隨機。
一種被稱為bagging的技術被用來創建一個樹的集合,其中多個訓練集通過替換生成。
bagging技術採用隨機抽樣的方法將資料集劃分為N個樣本。然後,使用單一學習演算法在所有樣本上建立模型。之後透過並行投票或平均的方式將預測結果結合起來。

線性模型和基於樹的模型哪個更好?
該問題取決於你要解決的問題類型。
1.如果因變數和自變數之間的關係可以被一個線性模型很好地模擬,線性迴歸將優於基於樹的模型。
2.如果因變數和自變數之間存在高度的非線性且複雜的關係,樹模型將優於經典迴歸方法。
3.如果你需要建立一個容易理解的模型,決策樹模型總是比線性模型更好。決策樹模型比線性迴歸更容易理解!
使用Scikit-learn進行決策樹分類器建立
我採用的資料是從https://drive.google.com/open? id=1x1KglkvJxNn8C8kzeV96YePFnCUzXhBS下載的超市相關數據,首先使用下面的程式碼載入所有基本函式庫:
import numpy as np import matplotlib.pyplot as plt import pandas as pd
之後,我們採用下面的方式來載入資料集。它包括5個屬性,用戶id,性別,年齡,預估工資和購買情況。
data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()

#圖1資料集
我們只將年齡和預估工資作為我們的自變數X,因為性別和使用者ID等其他特徵是不相關的,對一個人的購買能力沒有影響,y是因變數。
feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
下一步是將資料集分離為訓練集和測試集。
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)
接下來執行特徵縮放
#
#feature scaling from sklearn.preprocessing import StandardScaler sc_X = StandardScaler() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
將模型擬合到決策樹分類器中。
from sklearn.tree import DecisionTreeClassifier classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
進行預測並檢查準確度。
#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))
決策樹分類器的準確率達到91%。
混淆矩陣
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)Output: array([[64,4], [ 2, 30]])
#這表示有6個觀測結果被列為錯誤。
首先,讓我們將模型預測結果視覺化
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()

#接下來,想像這棵樹
接下來您可以使用Scikit-learn的export_graphviz函數在Jupyter筆記本中顯示樹。為了繪製樹,我們需要採用下面的命令安裝Graphviz和pydotplus:
conda install python-graphviz pip install pydotplus
export_graphviz函數將決策樹分類器轉換為點文件,pydotplus將該點文件轉換為png或在Jupyter上顯示的形式,具體實作方式如下:
from sklearn.tree import export_graphviz from sklearn.externals.six import StringIO from IPython.display import Image import pydotplusdot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True,feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())

在决策树形图中,每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数,它代表了节点的纯度。当一个节点的所有记录都属于同一个类时,您可以说它是纯节点,这种节点称为叶节点。
在这里,生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中,我会通过修剪的方式来优化树。
随后优化决策树分类器
criteria: 该选项默认配置是Gini,我们可以通过该项选择合适的属性选择方法,该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。
splitter: 该选项默认配置是" best ",我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。
max_depth:默认配置是None,我们可以通过该参数设置树的最大深度。若设置为None,则节点将展开,直到所有叶子包含的样本小于min_samples_split。最大深度值越高,过拟合越严重,反之,过拟合将不严重。
在Scikit-learn中,只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。
# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
至此分类率提高到94%,相对之前的模型来说,其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。
dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())

上图是经过修剪后的模型,相对之前的决策树模型图来说,其更简单、更容易解释和理解。
总结
在本文中,我们讨论了很多关于决策树的细节,它的工作方式,属性选择措施,如信息增益,增益比和基尼指数,决策树模型的建立,可视化,并使用Python Scikit-learn包评估和优化决策树性能,这就是这篇文章的全部内容,希望你们能喜欢它。
译者介绍
赵青窕,51CTO社区编辑,从事多年驱动开发。
原文标题:Decision Tree Algorithm, Explained,作者:Nagesh Singh Chauhan
以上是剖析決策樹演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM
優化您的組織與Genai代理商的電子郵件營銷Apr 13, 2025 am 11:44 AM介紹 恭喜!您經營一家成功的業務。通過您的網頁,社交媒體活動,網絡研討會,會議,免費資源和其他來源,您每天收集5000個電子郵件ID。下一個明顯的步驟是
 Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM
Apache Pinot實時應用程序性能監視Apr 13, 2025 am 11:40 AM介紹 在當今快節奏的軟件開發環境中,確保最佳應用程序性能至關重要。監視實時指標,例如響應時間,錯誤率和資源利用率可以幫助MAIN
 Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM
Chatgpt擊中了10億用戶? Openai首席執行官說:'短短幾週內翻了一番Apr 13, 2025 am 11:23 AM“您有幾個用戶?”他扮演。 阿爾特曼回答說:“我認為我們上次說的是每週5億個活躍者,而且它正在迅速增長。” “你告訴我,就像在短短幾週內翻了一番,”安德森繼續說道。 “我說那個私人
 pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM
pixtral -12b:Mistral AI'第一個多模型模型 - 分析VidhyaApr 13, 2025 am 11:20 AM介紹 Mistral發布了其第一個多模式模型,即Pixtral-12b-2409。該模型建立在Mistral的120億參數Nemo 12B之上。是什麼設置了該模型?現在可以拍攝圖像和Tex
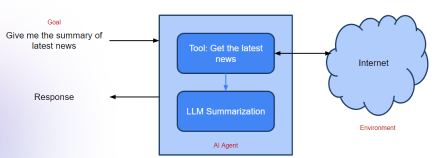 生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM
生成AI應用的代理框架 - 分析VidhyaApr 13, 2025 am 11:13 AM想像一下,擁有一個由AI驅動的助手,不僅可以響應您的查詢,還可以自主收集信息,執行任務甚至處理多種類型的數據(TEXT,圖像和代碼)。聽起來有未來派?在這個a


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境

SublimeText3 英文版
推薦:為Win版本,支援程式碼提示!

DVWA
Damn Vulnerable Web App (DVWA) 是一個PHP/MySQL的Web應用程序,非常容易受到攻擊。它的主要目標是成為安全專業人員在合法環境中測試自己的技能和工具的輔助工具,幫助Web開發人員更好地理解保護網路應用程式的過程,並幫助教師/學生在課堂環境中教授/學習Web應用程式安全性。 DVWA的目標是透過簡單直接的介面練習一些最常見的Web漏洞,難度各不相同。請注意,該軟體中

SublimeText3漢化版
中文版,非常好用

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能