用 Python 實現導彈自動追踪,超燃!
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB轉載
- 2023-04-12 08:04:051527瀏覽

大家好,我是J哥。
這個沒有點數學基礎是很難算出來的。但是我們有了計算機就不一樣了,依靠計算機極快速的運算速度,我們利用微分的思想,加上一點簡單的三角學知識,就可以實現它。
好,話不多說,我們來看看它的演算法原理,看圖:
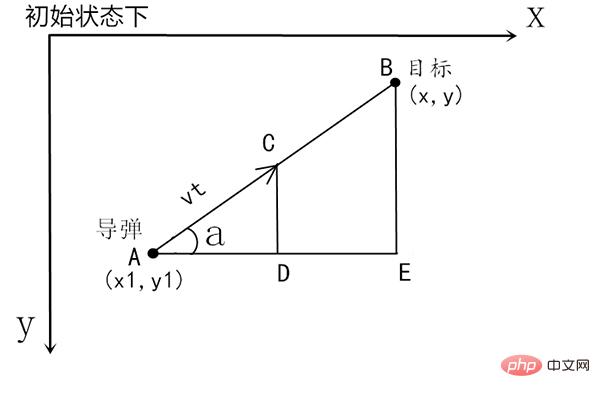
#由於待會要用pygame演示,它的座標係是y軸向下,所以這裡我們也用y向下的座標系。
演算法總的想法就是根據上圖,把時間t分割成足夠小的片段(例如1/1000,這個時間片越小越精確),每一個片段分別構造如上三角形,計算出飛彈下一個時間片走的方向(即∠a)和走的路程(即vt=|AC|),這時候目標再在第二個時間片移動了位置,這時剛才計算的C點又變成了第二個時間片的初始點,這時再在第二個時間片上在C點和新的目標點構造三角形計算新的vt,然後進入第三個時間片,如此反复即可。
假設飛彈和目標的初始狀態下座標分別是(x1,y1),(x,y),建構出直角三角形ABE,這個三角形用來求∠a的正弦和餘弦值,因為vt是自己設定的,我們需要計算A到C點x和y座標分別移動了多少,移動的值就是AD和CD的長度,這兩個分別用vt乘cos(a)和sin(a)即可。
計算sin(a)和cos(a),正弦對比斜,餘弦鄰比斜,斜邊可以利用兩點距離公式計算出,即:
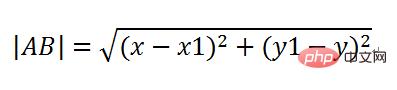
於是

AC的長度就是飛彈的速度乘以時間即|AC|=vt,然後即可計算出AD和CD的長度,於是這一個時間片過去後,飛彈應該出現在新的位置C點,他的座標就是老的點A的x增加AD和y減去CD。
於是,新的C點座標就是:
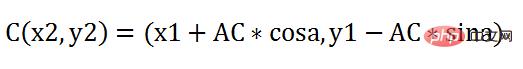
#只要一直反覆循環執行這個動作即可,好吧,為了更形象,把第一個時間片和第二個時間片放在一起看看:
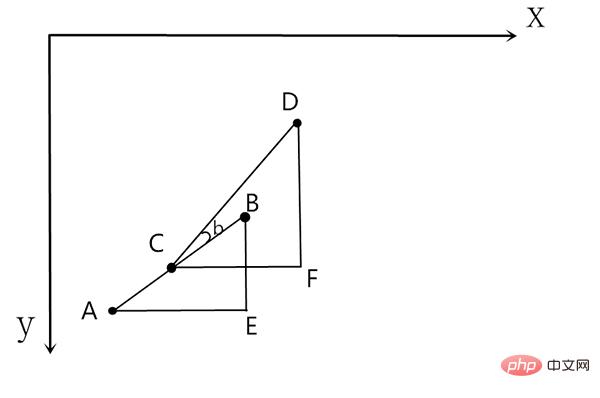
第一個是時間片建構的三角形是ABE,經過一個時間片後,目標從B點走到了D點,導彈此時在C點,於是構造新的三角形CDF,重複剛才的計算過程即可,圖中的角∠b就是導彈需要旋轉的角度,現實中只需要每個時間片修正飛彈的方向就可以了,具體怎麼讓飛彈改變方向,這就不是我們需要研究的問題了
好,由於最近在用Python的pygame庫製作小遊戲玩,接下來我們就用pygame來示範這個效果,效果如下圖:

很簡單的程式碼如下:
import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
old_angle=0
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置,鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点线段的弧度值
x1,y1=(x1+section*cosa,y1-section*sina)
d_angle = degrees(angle)#弧度转角度
screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
dis_angle=d_angle-old_angle#dis_angle就是到下一个位置需要改变的角度
old_angle=d_angle#更新初始角度
pygame.display.update()
如果只把飛彈考慮為一個質點的話,那麼以上演算法就已經足矣,我沒有做導彈的旋轉,因為一個質點也不分頭尾不需要旋轉,當然這前提得是你加載的導彈圖片很小的時候不旋轉看起來也沒什麼問題。但是在pygame裡面做旋轉並不是一件容易的事情,我們先把圖片替換成一張矩形的,再加入旋轉函數看看效果如何

missiled = pygame.transform.rotate(missile, -(d_angle)) screen.blit(missiled, (x1-missile.get_width(), y1- missile.get_height()/2))
因為圖片的座標點是它的左上角的點,所以如果我們想讓圖片的座標固定在箭頭尖點,那麼把圖片實際列印位置x減少圖片長度,y減少一半寬度就行。但是實際運行效果並不好:

大致方向相同,但是图片箭头的尖点并没有一直跟随鼠标,这是为什么呢。经过一番研究,我发现原来是这个图旋转的机制问题,我们看看旋转后的图片变成什么样了:
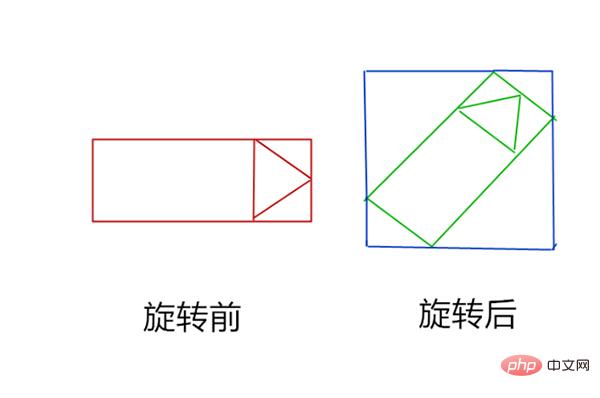
旋转后的图片变成了蓝色的那个范围,根据旋转角度的不同,所变成的图片大小也不一样,我们看旋转90的情况
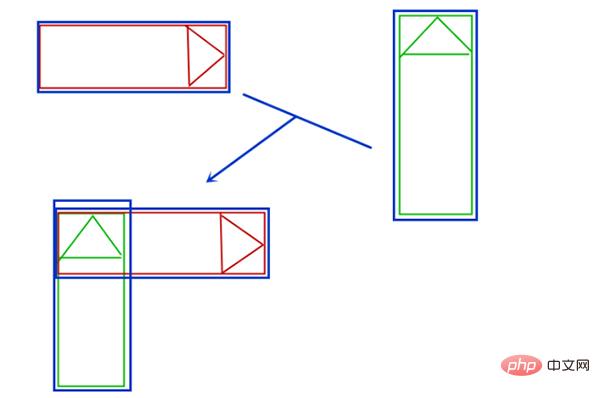
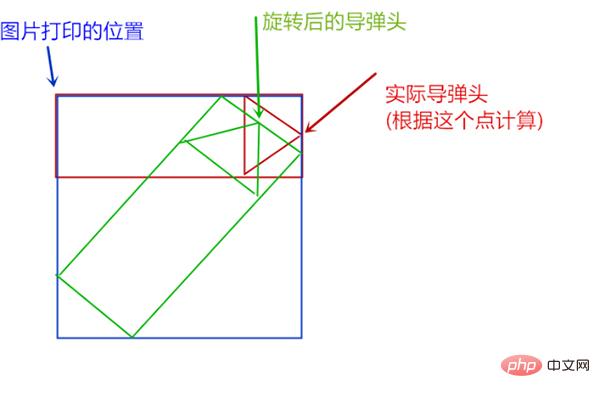
我们发现,旋转后的图片不仅面积变大了,导弹头的位置也变了。那应该怎么解决这个问题呢?思路是,每一次旋转图片以后,求出旋转图的头位置(图中的绿色箭头点),然后把绿图的打印位置移动一下,下,x,y分别移动两个头的距离,就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置,移动后应该是这样的:
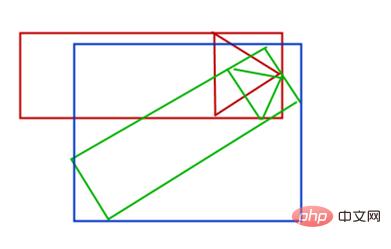
这样,两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同,旋转角在不同象限参数不一样,所以我们分为这四种情况
1,2象限
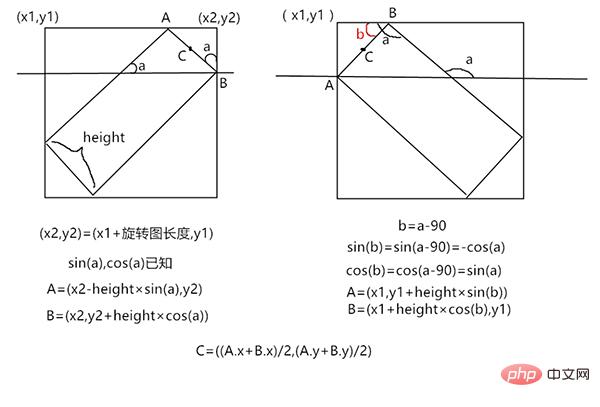
3,4象限,它的旋转只有正负0—180,所以3,4象限就是负角
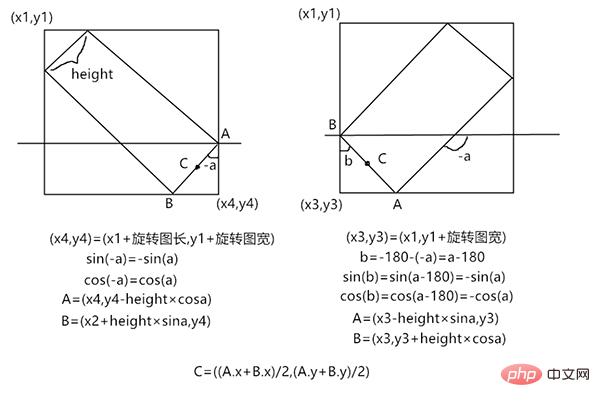
显示图片的时候我们将他移动
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)
所以最后我们加入相关算法代码,效果就比较完美了

大功告成,最后附上全部的算法代码
import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置,鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()
以上便是用Python模拟导弹自动追踪的代码实例。
以上是用 Python 實現導彈自動追踪,超燃!的詳細內容。更多資訊請關注PHP中文網其他相關文章!

