資料科學家必須了解的六大聚類演算法

目前如Google新聞等許多應用都將聚類演算法作為主要的實現手段，它們能利用大量的未標註資料來建構強大的主題聚類。本文從最基礎的 K 均值聚類到基於密度的強大方法介紹了 6 類主流方法，它們各有擅長領域與情景，且基本思想並不一定限於聚類方法。

本文將從簡單且有效率的K 均值聚類開始，依序介紹均值漂移聚類、基於密度的聚類、利用高斯混合和最大期望方法聚類、層次聚類和適用於結構化資料的圖團體檢測。我們不僅會分析基本的實作概念，同時還會給出每種演算法的優缺點以明確實際的應用場景。

聚類是一種包含資料點分組的機器學習技術。給定一組資料點，我們可以用聚類演算法將每個資料點分到特定的群組中。理論上，屬於同一組的資料點應該有相似的屬性和/或特徵，而屬於不同組的資料點應該有非常不同的屬性和/或特徵。聚類是一種無監督學習的方法，是一種在許多領域常用的統計資料分析技術。

K-Means（K 均值）聚類

K-Means 可能是最知名的聚類演算法。它是許多入門級資料科學和機器學習課程的內容。在程式碼中很容易理解和實現！請看下面的圖。

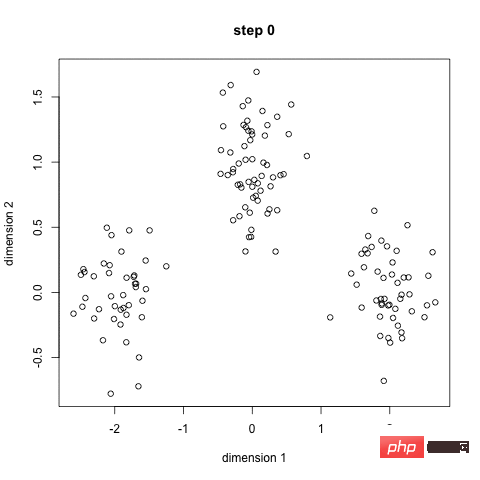
K-Means 聚類

首先，我們選擇一些類別/群組，並隨機初始化它們各自的中心點。為了算出要使用的類別的數量，最好快速查看數據，並嘗試識別不同的群組。中心點是與每個資料點向量長度相同的位置，在上圖中是「X」。

透過計算資料點與每個群組中心之間的距離來對每個點進行分類，然後將該點歸類於群組中心與其最接近的群組中。

根據這些分類點，我們利用群組中所有向量的平均值來重新計算群組中心。

重複這些步驟來進行一定數量的迭代，或直到組中心在每次迭代後的變化不大。你也可以選擇隨機初始化組中心幾次，然後選擇看起來提供了最佳結果的運行。

K-Means 的優點在於速度快，因為我​​們真正在做的是計算點和群組中心之間的距離：非常少的計算！因此它具有線性複雜度 O(n)。

另一方面，K-Means 有一些缺點。首先，你必須選擇有多少組/類。這並不總是仔細的，而且理想情況下，我們希望聚類演算法能夠幫我們解決分成多少類的問題，因為它的目的是從資料中獲得一些見解。 K-means 也從隨機選擇的聚類中心開始，所以它可能在不同的演算法中產生不同的聚類結果。因此，結果可能不可重複並缺乏一致性。其他聚類方法則更加一致。

K-Medians 是與 K-Means 有關的另一個聚類演算法，除了不是用均值而是用組的中位數向量來重新計算組中心。這種方法對異常值不敏感（因為使用中位數），但對於較大的資料集要慢得多，因為在計算中值向量時，每次迭代都需要進行排序。

均值漂移聚類

均值漂移聚類是基於滑動視窗的演算法，它試圖找到資料點的密集區域。這是一個基於質心的演算法，這意味著它的目標是定位每個群組/類別的中心點，透過將中心點的候選點更新為滑動視窗內點的平均值來完成。然後，在後處理階段對這些候選視窗進行過濾以消除近似重複，形成最終的中心點集及其對應的群組。請看下面的圖例。

平均值漂移聚類用於單一滑動視窗

1. 為了解釋平均值漂移，我們將考慮二維空間中的一組點，如上圖所示。我們從以 C 點（隨機選擇）為中心，以半徑 r 為核心的圓形滑動視窗開始。均值漂移是一種爬山演算法，它包括在每一步中迭代地向更高密度區域移動，直到收斂。
2. 在每次迭代中，滑動視窗透過將中心點移向視窗內點的平均值（因此而得名）來移向更高密度區域。滑動視窗內的密度與其內部點的數量成正比。自然地，透過向視窗內點的平均值移動，它會逐漸移向點密度較高的區域。
3. 我們繼續按照平均值移動滑動視窗直到沒有方向在核內可以容納更多的點。請看上面的圖；我們一直移動這個圓直到密度不再增加（即視窗中的點數）。
4. 步驟 1 到 3 的過程是透過許多滑動視窗完成的，直到所有的點都位於一個視窗內。當多個滑動視窗重疊時，保留包含最多點的視窗。然後根據資料點所在的滑動視窗進行聚類。

下面顯示了所有滑動視窗從頭到尾的整個過程。每個黑點代表滑動視窗的質心，每個灰點代表一個資料點。

均值漂移聚類的整個過程

與K-means 聚類相比，這種方法不需要選擇簇數量，因為均值漂移自動發現這一點。這是一個巨大的優勢。聚類中心朝最大點密度聚集的事實也是非常令人滿意的，因為理解和適應自然資料驅動的意義是非常直觀的。它的缺點是視窗大小/半徑“r”的選擇可能是不重要的。

基於密度的聚類方法（DBSCAN）

DBSCAN 是一種基於密度的聚類演算法，它類似於平均值漂移，但具有一些顯著的優點。請看下面的另一個有趣的圖形，讓我們開始吧！

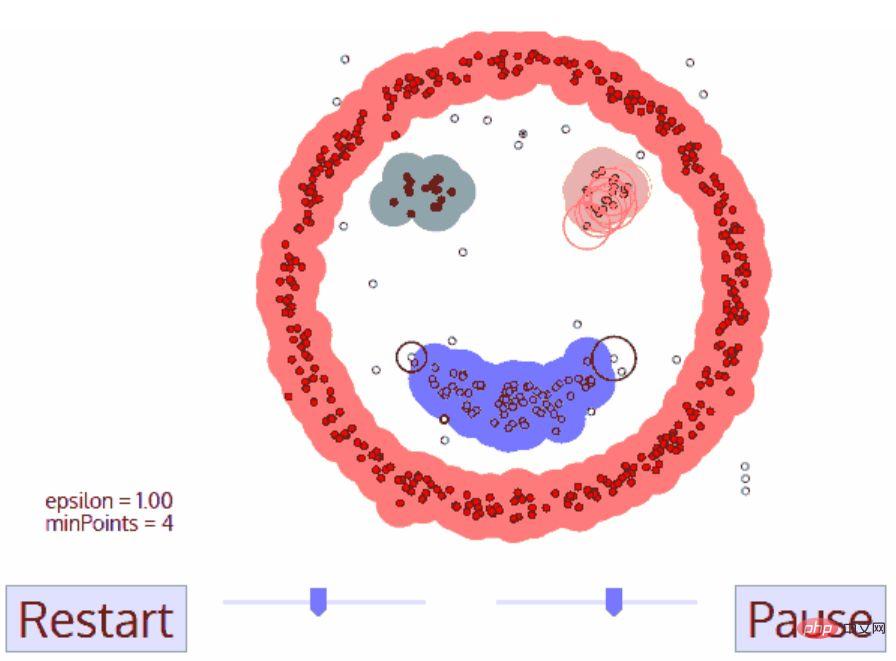
DBSCAN 聚類

1. DBSCAN 從一個沒有被存取的任意起始資料點開始。這個點的鄰域是用距離 ε（ε 距離內的所有點都是鄰域點）提取的。
2. 如果在這個鄰域內有足夠數量的點（根據 minPoints），則聚類過程開始，並且當前資料點成為新簇的第一個點。否則，該點將會被標記為雜訊（稍後這個雜訊點可能仍會成為聚類的一部分）。在這兩種情況下，該點都被標記為“已訪問”。
3. 對於新簇中的第一個點，其 ε 距離鄰域內的點也成為該簇的一部分。這個使所有 ε 鄰域內的點都屬於同一個簇的過程將對所有剛剛添加到簇中的新點重複。
4. 重複步驟 2 和 3，直到簇中所有的點都被確定，即簇的 ε 鄰域內的所有點都被存取和標記過。
5. 一旦我們完成了當前的簇，一個新的未訪問點將被檢索和處理，導致發現另一個簇或雜訊。重複這個過程直到所有的點被標記為已訪問。由於所有點都已經被訪問，所以每個點都屬於某個簇或雜訊。

DBSCAN 與其他聚類演算法相比有很多優點。首先，它根本不需要固定數量的簇。它也會將異常值識別為噪聲，而不像均值漂移，即使資料點非常不同，也會簡單地將它們分入簇中。另外，它能夠很好地找到任意大小和任意形狀的簇。

DBSCAN 的主要缺點是當簇的密度不同時，它的表現不如其他聚類演算法。這是因為當密度變化時，用於識別鄰域點的距離閾值 ε 和 minPoints 的設定將會隨著簇而變化。這個缺點也會在非常高維度的資料中出現，因為距離閾值 ε 再次變得難以估計。

用高斯混合模型（GMM）的最大期望值（EM）聚類

K-Means 的一個主要缺點是它對於聚類中心平均值的簡單使用。透過下面的圖，我們可以明白為什麼這不是最佳方法。在左側，可以非常清楚的看到有兩個具有不同半徑的圓形簇，以相同的平均值作為中心。 K-Means 不能處理這種情況，因為這些簇的平均值是非常接近的。 K-Means 在簇不是圓形的情況下也失敗了，同樣是由於使用平均值作為聚類中心。

K-Means 的兩個失敗案例

高斯混合模型（GMMs）比 K-Means 給了我們更多的靈活性。對於 GMMs，我們假設資料點是高斯分佈的；相對於使用平均值來假設它們是圓形的，這是一個限制較少的假設。這樣，我們有兩個參數來描述簇的形狀：平均值和標準差！以二維為例，這意味著，這些簇可以採取任何類型的橢圓形（因為我們在 x 和 y 方向都有標準差）。因此，每個高斯分佈被分配給單一簇。

為了找出每個簇的高斯參數（例如平均值和標準差），我們將使用一個稱為最大期望（EM）的最佳化演算法。請看下面的圖表，這是一個高斯適合於群集的例子。然後我們可以使用 GMMs 繼續進行最大期望聚類的過程。

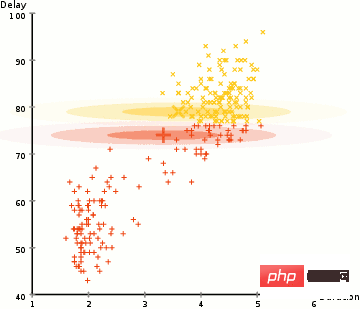
使用GMMs 的EM 聚類

1. 我們首先選擇簇的數量（如K-Means 所做的），並隨機初始化每個簇的高斯分佈參數。也可以透過快速查看數據來嘗試為初始參數提供一個好的猜測。但請注意，正如上圖所看到的，這不是 100% 必要的，因為高斯開始時我們很窮，但是很快就得到了優化。
2. 給定每個簇的高斯分佈，計算每個資料點屬於一個特定簇的機率。一個點越靠近高斯的中心，它就越可能屬於該簇。這應該是很直觀的，因為對於高斯分佈我們假設大部分資料更靠近簇的中心。
3. 基於這些機率，我們計算一組新的高斯分佈參數使得簇內的資料點的機率最大化。我們使用資料點位置的加權和來計算這些新參數，其中權重是資料點屬於該特定簇的機率。為了用可視化的方式解釋它，我們可以看一下上面的圖，特別是黃色的簇，我們以它作為例子。分佈在第一次迭代時隨即開始，但我們可以看到大部分的黃點都在分佈的右邊。當我們計算一個機率加權和時，即使中心附近有一些點，但它們大部分都在右側。因此，分佈的平均值自然會接近這些點。我們也可以看到大部分的點分佈在「從右上到左下」。因此改變標準差來創建更適合這些點的橢圓，以便最大化機率加權和。
4. 重複步驟 2 和 3 直到收斂，其中分佈在迭代中的變化不大。

使用 GMMs 有兩個關鍵的優勢。首先，GMMs 比 K-Means 在簇協方差方面更靈活；因為標準差參數，簇可以呈現任何橢圓形狀，而不是被限制為圓形。 K-Means 實際上是 GMM 的一個特殊情況，這種情況下每個簇的協方差在所有維度都接近 0。第二，因為 GMMs 使用機率，所以每個資料點可以有很多簇。因此如果一個資料點在兩個重疊的簇的中間，我們可以簡單地透過說它百分之 X 屬於類別 1，百分之 Y 屬於類別 2 來定義它的類別。即 GMMs 支援混合資格。

凝聚層次聚類

層次聚類演算法其實分為兩類：自上而下或自下而上。自下而上的演算法首先將每個資料點視為單一的簇，然後連續合併（或聚合）兩個簇，直到所有的簇都合併成一個包含所有資料點的簇。因此，自下而上層次聚類稱為凝聚式層次聚類或 HAC。這個簇的層次用樹（或樹狀圖）表示。樹的根是收集所有樣本的唯一簇，葉是僅具有一個樣本的簇。在進入演算法步驟前，請看下面的圖例。

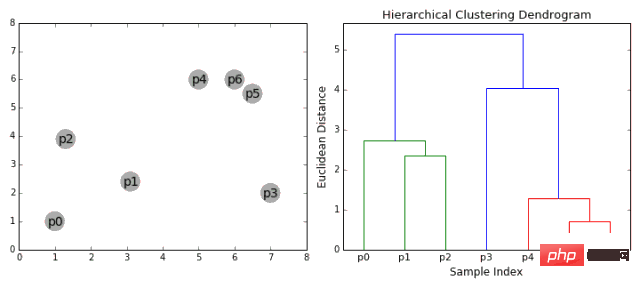
凝聚式層次聚類

1. 我們首先將每個資料點視為一個單一的簇，即如果我們的資料集中有 X 個資料點，那麼我們就有 X 個簇。然後，我們選擇一個測量兩個簇之間距離的距離測量標準。作為例子，我們將使用 average linkage，它將兩個簇之間的距離定義為第一個簇中的資料點與第二個簇中的資料點之間的平均距離。
2. 在每次迭代中，我們將兩個簇合併成一個。這兩個要合併的群集應具有最小的 average linkage。即根據我們選擇的距離度量標準，這兩個簇之間的距離最小，因此是最相似的，應該合併在一起。
3. 重複步驟 2 直到我們到達樹根，也就是我們只有一個包含所有資料點的簇。這樣我們只需要選擇何時停止合併簇，即何時停止建造樹，來選擇最終需要多少個簇！

層次聚類不需要我們指定簇的數量，我們甚至可以選擇哪個數量的簇看起來最好，因為我們正在建立一棵樹。另外，該演算法對於距離度量標準的選擇並不敏感；他們都同樣表現得很好，而對於其他聚類演算法，距離度量標準的選擇是至關重要的。層次聚類方法的一個特別好的例子是當基礎資料具有層次結構，並且你想要恢復層次時；其他聚類演算法不能做到這一點。與 K-Means 和 GMM 的線性複雜度不同，層次聚類的這些優點是以較低的效率為代價的，因為它具有 O(n³) 的時間複雜度。

圖形團體偵測（Graph Community Detection）

當我們的資料可以被表示為一個網路或圖（graph）時，我們可以使用圖團體偵測方法完成聚類。在這個演算法中，圖團體（graph community）通常被定義為一種頂點（vertice）的子集，其中的頂點相對於網路的其它部分要連接得更加緊密。

也許最直覺的案例就是社群網路。其中的頂點表示人，連接頂點的邊表示他們是朋友或互粉的用戶。但是，若要將一個系統建模成一個網絡，我們就必須找到一種有效連接各個不同組件的方式。將圖論用於聚類的一些創新應用包括：對影像資料的特徵提取、分析基因調控網絡（gene regulatory networks）等。

下面是一個簡單的圖，展示了最近瀏覽過的 8 個網站，根據他們的維基百科頁面中的連結進行了連接。

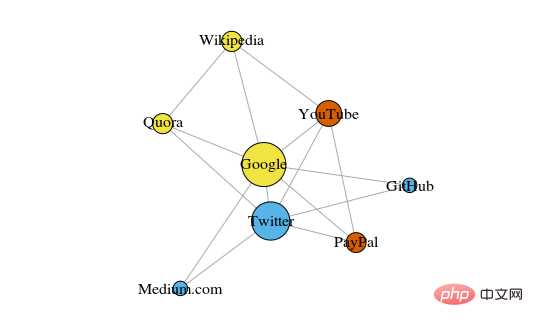
這些頂點的顏色表示了它們的團體關係，大小是根據它們的中心度（centrality）來決定的。這些聚類在現實生活中也很有意義，其中黃色頂點通常是參考/搜尋網站，藍色頂點全部是在線發佈網站（文章、微博或代碼）。

假設我們已經將該網路聚類變成了一些團體。我們就可以使用該模組性分數來評估聚類的品質。分數較高表示我們將該網路分割成了「準確的（accurate）」團體，而低分則表示我們的聚類更接近隨機。如下圖所示：

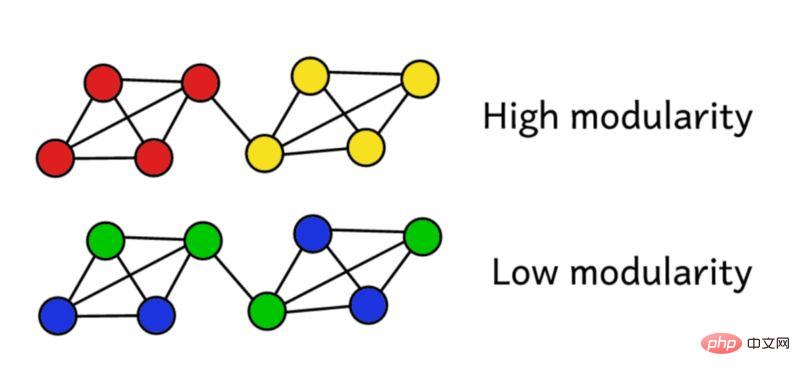
模組性可以使用以下公式進行計算：

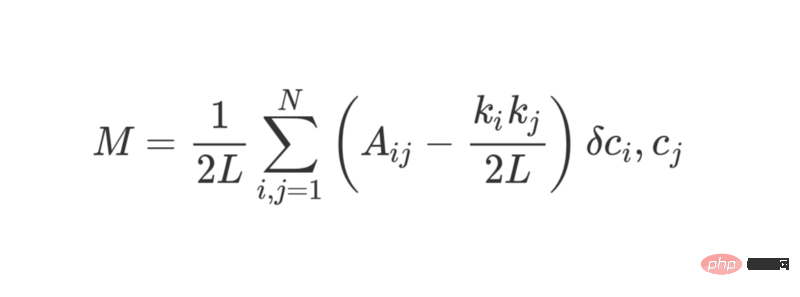
其中L 代表網路中邊的數量，k_i 和k_j 是指每個頂點的degree，它可以透過將每一行和每一列的項加起來而得到。兩者相乘再除以 2L 表示當該網路是隨機分配的時候頂點 i 和 j 之間的預期邊數。

整體而言，括號中的項表示了該網路的真實結構和隨機組合時的預期結構之間的差。研究它的值可以發現，當 A_ij = 1 且 ( k_i k_j ) / 2L 很小時，其傳回的值最高。這意味著，當在定點 i 和 j 之間存在一個「非預期」的邊時，得到的值更高。

最後的 δc_i, c_j 就是大名鼎鼎的克羅內克 δ 函數（Kronecker-delta function）。以下是其 Python 解釋：

透過以上公式可以計算圖的模組性，且模組性越高，此網路聚集成不同團體的程度就越好。因此透過最優化方法尋找最大模組性就能發現聚類此網路的最佳方法。

組合學（combinatorics）告訴我們對於一個僅有 8 個頂點的網絡，就存在 4140 種不同的聚類方式。 16 個頂點的網路的聚類方式將超過 100 億種。 32 個頂點的網絡的可能聚類方式更是將超過128 septillion（10^21）種；如果你的網絡有80 個頂點，那麼其可聚類的方式的數量就已經超過了可觀測宇宙中的原子數。

因此，我們必須求助於一種啟發式的方法，該方法在評估可以產生最高模組性分數的聚類上效果良好，而且並不需要嘗試每一種可能性。這是一種被稱為 Fast-Greedy Modularity-Maximization（快速貪婪模組性最大化）的演算法，這種演算法在一定程度上類似於上面描述的 agglomerative hierarchical clustering algorithm（集聚層次聚類演算法）。只是 Mod-Max 並不根據距離（distance）來融合團體，而是根據模組性的改變來對團體進行融合。

以下是其工作方式：

• 首先初始分配每個頂點到自己的團體，然後計算整個網路的模組性 M。
• 第 1 步要求每個團體對（community pair）至少被一條單邊鏈接，如果有兩個團體融合到了一起，該演算法就計算由此造成的模組性改變 ΔM。
• 第 2 步是取 ΔM 出現了最大成長的團體對，然後融合。然後為這個聚類計算新的模組性 M，並記錄下來。
• 重複第 1 步和 第 2 步－每一次都融合團體對，這樣最後得到 ΔM 的最大增益，然後記錄新的聚類模式及其對應的模組性分數 M。
• 當所有的頂點都被分成了一個巨型聚類時，就可以停止了。然後演算法會檢查這個過程中的記錄，然後找到其中傳回了最高 M 值的聚類模式。這就是返回的團體結構。

團體檢測（community detection）是現在圖論中一個熱門的研究領域，它的限制主要體現在會忽略一些小的集群，且只適用於結構化的圖模型。但這一類演算法在典型的結構化資料中和現實網狀資料都有非常好的效能。

結語

以上就是資料科學家應該知道的 6 大聚類演算法！我們將以展示各類演算法的視覺化效果來結束本文！

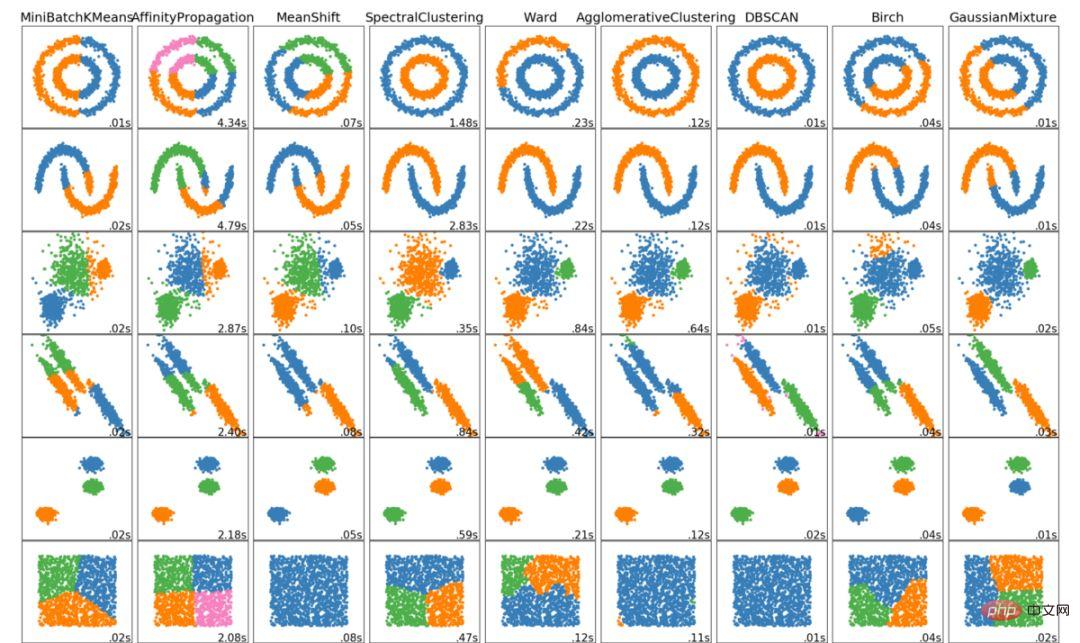
以上是資料科學家必須了解的六大聚類演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！