自動駕駛決策規劃技術詳解

隨著深度強化學習技術的快速發展，越來越多的研究團隊開始將其應用於自動駕駛決策規劃中，將行為決策與運動規劃模組融合，直接學習得到行車軌跡。

自動駕駛中的決策規劃模組是衡量和評估自動駕駛能力最核心的指標之一，它的主要任務是在接收到感測器的各種感知資訊之後，對當前環境作出分析，然後對底層控制模組下達指令。典型的決策規劃模組可分為三個層次：全域路徑規劃、行為決策、運動規劃。

01 引言

在一套完整的自動駕駛系統中，如果將感知模組比喻為人的眼睛和耳朵，那麼決策規劃就是自動駕駛的大腦。大腦在接收到感測器的各種感知資訊之後，對當前環境作出分析，然後對底層控制模組下達指令，這個過程就是決策規劃模組的主要任務。同時，決策規劃模組可以處理多麼複雜的場景，也是衡量和評估自動駕駛能力最核心的指標之一[1]。

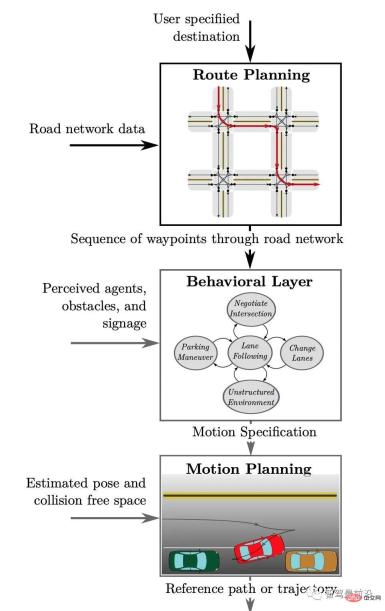
圖1.  自動駕駛系統中的決策規劃模組分層結構，引用自[2]

如圖1所示，典型的決策規劃模組可以分為三個層次。

其中，全域路徑規劃（Route Planning）在接收到一個給定的行駛目的地之後，結合地圖信息，生成一條全局的路徑，作為為後續具體路徑規劃的參考；

行為決策層（Behavioral Layer）在接收到全域路徑後，結合從感知模組得到的環境資訊（包括其他車輛與行人，障礙物，以及道路上的交通規則資訊），做出具體的行為決策（例如選擇變換車道超車或跟隨）；

最後，運動規劃（Motion Planning）層根據具體的行為決策，規劃產生一條滿足特定約束條件（例如車輛本身的動力學約束、避免碰撞、乘客舒適性等）的軌跡，該軌跡作為控制模組的輸入決定車輛最終行駛路徑。

本文將分別介紹各層的主要作用與共同演算法，並且比較各種演算法的優劣性及適用情境。

02 全域路徑規劃（Route Planning） 

全域路徑規劃是指在給定車輛目前位置與終點目標後，透過搜尋選擇一條最優的路徑，這裡的「最優」包括路徑最短，或到達時間最快等條件。這個過程類似於我們生活中經常用到的「導航」功能，區別在於自動駕駛中使用的高精地圖與我們常見的地圖不太一樣，在高精地圖中包含了每條車道在內的更多資訊。常見的全域路徑規劃演算法包括Dijkstra和A演算法，以及在這兩種演算法基礎上的多種改進。 Dijkstra演算法[3]和A*演算法[4]也是在許多規劃問題中應用最廣泛的兩種搜尋演算法。

圖2.全域路徑規劃示意圖

#1. Dijkstra演算法

Dijkstra演算法是由電腦科學家Edsger W. Dijkstra在1956年提出，用來尋找圖形中節點之間的最短路徑。在Dijkstra演算法中，需要計算每一個節點距離起點的總移動代價。同時，還需要一個優先隊列結構。對於所有待遍歷的節點，放入優先佇列中會依照代價進行排序。在演算法運行的過程中，每次都從優先隊列中選出代價最小的作為下一個遍歷的節點。直到到達終點為止。

Dijkstra演算法的優點是：給出的路徑是最優的；缺點是計算時間複雜度比較高（O(N2)）,因為是向周圍進行探索，沒有明確的方向。

2. A*演算法

為了解決Dijkstra演算法的搜尋效率問題，1968年，A演算法由Stanford研究院的Peter Hart, Nils Nilsson以及Bertram Raphael發表，其主要改進是藉助一個啟發函數來引導搜尋的過程。具體來說，A演算法透過下面這個函數來計算每個節點的優先權:

f(n)=g(n) h(n)

其中：

• f(n) 是節點n的綜合優先權。當我們選擇下一個要遍歷的節點時，我們總是會選取綜合優先權最高（值最小）的節點。
• g(n)是節點n距離起點的代價。
• h(n) 是節點n距離終點的預期代價，這也就是A*演算法的啟發函數。

03 行為決策（Behavioral Layer）

在確定全域路徑之後，自動駕駛車輛需要根據特定的道路狀況、交通規則、其他車輛與行人等情況作出合適的行為決策。

這個過程面臨三個主要問題：

首先，真實的駕駛場景千變萬化，如何覆蓋？

其次，真實的駕駛場景是一個多智能體決策環境，包括主車在內的每個參與者所做的行為，都會對環境中的其他參與者帶來影響，因此我們需要對環境中其他參與者的行為進行預測；

最後，自動駕駛車輛對於環境資訊不可能做到100%的感知，例如存在許多被障礙物遮蔽的可能危險情況。

綜合以上幾點，在自動駕駛行為決策層，我們需要解決的是在多智能體決策的複雜環境中，存在著感知不確定性情況的規劃問題。可以說這個難題是真正實現L4、L5級自動駕駛技術的核心瓶頸之一，近年來隨著深度強化學習等領域的快速發展，為解決這個問題帶來了新的思維和曙光。

以下將行為決策層的模型分為四類分別介紹[5]：

#1. 有限狀態機模型

自動駕駛車輛最開始的決策模型為有限狀態機模型[6]，車輛根據當前環境選擇適當的駕駛行為，如停車、換道、超車、避讓、緩慢行駛等模式，狀態機模型透過建構有限的有向連通圖來描述不同的駕駛狀態以及狀態之間的轉移關係，從而根據駕駛狀態的遷移反應式地產生駕駛動作。

有限狀態機模型因為簡單、易行，是無人駕駛領域目前最廣泛的行為決策模型，但該類別模型忽略了環境的動態性和不確定性，此外，當駕駛場景特徵較多時，狀態的劃分與管理較為繁瑣，多適用於簡單場景下，很難勝任具有豐富結構化特徵的城區道路環境下的行為決策任務。

2. 決策樹模型

決策/行為樹模型[7]和狀態機模型類似，也是透過目前駕駛狀態的屬性值反應式地選擇不同的駕駛動作，但不同的是該類模型將駕駛狀態和控制邏輯固化到了樹形結構中，透過自頂向下的「輪詢」機制進行駕駛策略搜尋。這類決策模型具備可視化的控制邏輯，且控制節點可重複使用，但需要針對每個駕駛場景離線定義決策網路，當狀態空間、行為空間較大時，控制邏輯將較為複雜。另外，此類模型同樣無法考慮交通環境中存在的不確定性因素。

3. 基於知識的推理決策模型

基於知識的推理決策模型由「場景特徵－駕駛動作」的映射關係來模仿人類駕駛員的行為決策過程，該類別模型將駕駛知識儲存在知識庫或神經網路中，這裡的駕駛知識主要表現為規則、案例或場景特徵到駕駛動作的映射關係。進而，透過「查詢」機制從知識庫或受過訓練的網路結構中推理出駕駛動作。

此類別模型主要包括：基於規則的推理系統[8]、基於案例的推理系統[9]和基於神經網路的映射模型[10]。

該類模型對先驗駕駛知識、訓練資料的依賴性較大，需要對駕駛知識進行精心整理、管理和更新，雖然基於神經網路的映射模型可以省去資料標註和知識整合的過程，但是仍有以下缺點：

• 其「資料」驅動機制使得其對訓練資料的依賴性較大，訓練資料需要足夠充分[11]；
• #將映射關係固化到網絡結構中，其解釋性較差；
• 存在「黑箱」問題，透明性差，對於實際系統中出現的問題可追溯性較差，很難發現問題的根本原因。

4. 基於價值的決策模型

根據最大效用理論，基於效用／價值的決策模型的基本思想是依據選擇準則在多個備選方案中選擇出最優的駕駛策略／動作[12]。

為了評估每個駕駛動作的好壞程度，該類別模型定義了效用（utility）或價值（value）函數，根據某些準則屬性定量地評估駕駛策略符合駕駛任務目標的程度，對於無人駕駛任務而言，這些準則屬性可以是安全性、舒適度、行車效率等，效用和價值可以由其中單一屬性決定也可以由多個屬性決定。

澳洲格里菲斯大學的Furda和Vlacic提出了多準則決策方法從候選動作集中選擇最優的駕駛動作[13]；新加坡國立大學的Bandyopadhyay等人提出了基於POMDP的行為決策模型[14]，以解決存在感知不確定性的情況；卡內基美隆大學的Wei J等人提出基於PCB（Prediction and-Cost-function Based）的行為決策模型[15]，其重點在於如何建構恰當的代價函數來引導對環境的預測；為了解決在多智能體參與的複雜環境中的決策問題，許多基於博弈論的模型也被研究者用來推理車輛之間的交互行為[16 ]，[17]；此外，因為在特徵提取方面的優勢，深度強化學習技術也開始被廣泛應用，以完成最優駕駛動作的生成[18]。

04 運動規劃（Motion Planning）

在確定具體的駕駛行為之後，我們需要做的是將“行為”轉化成一條更加具體的行駛“軌跡”，從而能夠最終產生對車輛的一系列具體控制訊號，實現車輛依照規劃目標的行駛。這個過程稱為運動規劃（Motion Planning），運動規劃的概念在機器人領域已經有較長的研究歷史，我們可以從數學的角度將它看做如下的一個最佳化問題：

#路徑規劃（Path Planning）

圖3.路徑規劃的定義

在以機器人為代表的許多場景中，我們可以認為周圍的環境是確定的。在這種情況下，所謂的路徑規劃，是指在給定的一個狀態空間Χ，尋找一個滿足一定約束條件的映射σ:[0,1]➞Χ，這些限制包括：

• 確定的起始狀態以及目標點所在的區域
• 避免碰撞
• 對路徑的微分約束（例如在實際問題中路徑曲率不能太小，對應於其二階導數的限制）

此最佳化問題的目標泛函定義為J(σ)，其具體意義可表示為路徑長度、控制複雜度等衡量標準。

然而在自動駕駛問題中，車輛周圍的環境是持續動態變化的，因此單純的路徑規劃不能給出在行駛過程中一直有效的解，因此我們需要增加一個維度－時間T ，相應的規劃問題通常被稱為軌跡規劃。

軌跡規劃（Trajectory Planning）

#圖 4.軌跡規劃的定義

時間維度的增加為規劃問題帶來了巨大的挑戰。例如，對於一個在2D環境中移動一個抽象化為單點的機器人，環境中的障礙物近似為多邊形的問題。路徑規劃問題可以在多項式時間內求解，而加入時間維度的軌跡規劃問題已被證明是NP-hard問題。

在自動駕駛的實際場景中，無論是對車輛本身還是對周圍環境，建立更為精確的模型意味著對最佳化問題更為複雜的約束，同時也意味著求解的更加困難。因此實際採用的演算法都是建立在實際場景的近似前提下，在模型精確性和求解效率二者之間尋求一個最佳的平衡點。

下文對自動駕駛領域目前常見的幾類運動規劃演算法分別進行介紹，在實際中，往往是其中幾類思想的結合才能最終達到比較好的規劃結果，並滿足更多的不同場景。

1. 基於搜尋的規劃演算法

透過搜尋來解決運動規劃問題是最樸素的思路之一,其基本思想是將狀態空間透過確定的方式離散成一個圖,然後利用各種啟發式搜尋演算法搜尋可行解甚至是最優解。      

在將狀態空間離散化的過程中，需要注意的是確保最終形成的柵格具有最大的覆蓋面積，同時不會重複。如圖5所示，左邊的柵格是由直行、左轉90°、右轉90°這三種行為產生；而如果選擇直行、左轉89°、右轉89°三種行為，最後就無法產生一個覆蓋全部區域的柵格結構。

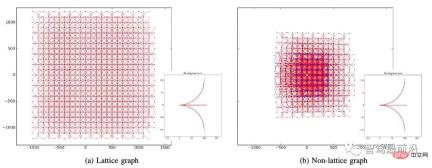
圖5. 建構柵格圖，引用自[2]

#在將狀態空間柵格化之後，我們就可以使用前文已經介紹的Dijkstra、 A*搜尋演算法，完成最終的規劃。然而在實際複雜環境中，柵格數目眾多，且環境隨時間動態變化，會導致搜尋結點過多，因此發展出了多種改進演算法，用以處理不同的具體場景：

1） Hybrid A* 演算法，在A*演算法的基礎上考慮了車的最大轉向問題，例如限定計算的路徑上車最大轉向不超過5°。該演算法目前的應用場景有車掉頭（Stanford 參加DARPA 挑戰賽使用的Junior車採用了該演算法進行uturn），泊車等等對方向盤控制要求較高的場景。

2）D*、D*Lite演算法，事先由終點向起點進行搜索，使用Dijkstra演算法，儲存路網中目標點到每個點的最短路徑長度k, 和該節點到目標點的實際長度值h，開始情況下k==h， 並且儲存每個節點的上一個節點，保證能夠沿著連結走下去。

計算結束後，取得了一條當時最優路徑。當車子行駛到某個節點時，透過感測器發現該節點已經無法通行（有障礙物），則對已儲存的路網資訊一些相關點的h值進行修改（變大），選擇一個鄰居點滿足仍然h==k的，即仍是最優路徑上的點，作為下一個點。

然後走到終點。此類演算法適用於在未知環境中的導航以及路徑規劃，廣泛用於目前各種移動機器人和自主車輛載具，例如「機遇號」和「勇氣號」火星車。

2. 基於取樣的規劃演算法

透過對連續的狀態空間進行取樣，從而將原始問題近似成一個離散序列的最佳化問題，這一思路也是在計算機科學中應用最廣泛的演算法。在運動規劃問題中，基於採樣的基本演算法包括機率路線圖(PRM)和快速搜尋隨機樹(RRT)演算法。

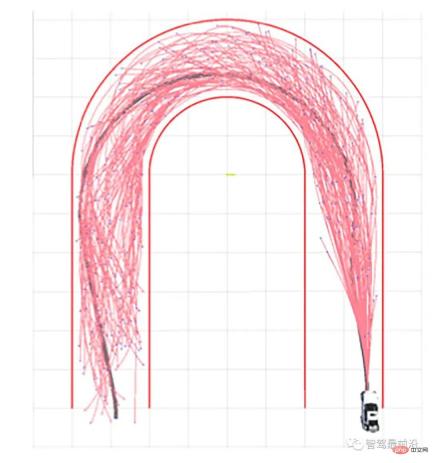
圖6.利用RRT演算法實現u形彎的軌跡規劃，引用自[19]

1）基本演算法：機率路線圖(PRM)

• 預處理階段：對狀態空間內的安全區域均勻隨機採樣n個點，每個採樣點分別與一定距離內的鄰近採樣點連接，並丟棄掉與障礙物發生碰撞的軌跡,最終得到一個連通圖。
• 査詢階段：對於給定的一對初始和目標狀態,分別將其連接到已經建構的圖中,再使用搜尋演算法尋找滿足要求的軌跡。

容易看出,一旦建構一個PRM之後,可以用於解決不同初始、目標狀態的運動規劃問題,但是這個特性對於自動駕駛運動規劃而言是不必要的。另外PRM要求對狀態之間進行精確連接，這對於存在複雜微分約束的運動規劃問題是十分困難的。

2） 基本演算法：快速搜尋隨機樹(RRT)

• #樹的初始化：初始化樹的結點集與邊集,結點集只包含初始狀態,邊集為空。
• 樹的生長：對狀態空間隨機採樣，當採樣點落在狀態空間安全區域時，選擇當前樹中離採樣點最近的結點，將其向採樣點擴展(或連接)。若產生的軌跡不會與障礙物發生碰撞，則將該軌跡加入樹的邊集，則該軌跡的終點加入到樹的結點集。

RRT是一種增量式取樣的搜尋方法，無須設定任何解析度參數。在極限情況，該搜尋樹將稠密的佈滿整個空間，此時搜尋樹由許多較短曲線或路經構成，以實現充滿整個空間的目的。

3）多種改進演算法

從上述基礎演算法的描述我們可以了解到，對狀態空間進行採樣，可以保證得到連接起始點與終點的可行解，但由於取樣過程是對整個空間進行均勻取樣，因此效率很低；在複雜場景下無法實現即時求解；此外，最終規劃結果無法保證得到的可行解是最優解。針對這些劣勢，多種改進演算法被提出並應用於自動駕駛問題：

• 效率改進--不均勻取樣

- RRT-Connect：同時建構兩棵分別起始於初始狀態和目標狀態的樹,當兩棵樹生長在一起時則找到可行解。

-  啟發式（hRRT）：使用啟發式函數增加擴展代價較低的結點被取樣的機率。

-  結合駕駛者模型：結合駕駛視覺注意力模型進行偏向性取樣，利用視覺特徵資訊引導運動規劃，使規劃出的軌跡更符合人類駕駛行為。

-  建構新度量RG-RRT(reachability guided RT)：常規類歐式距離的測量並不能真實反映構形或狀態之間的遠近，RG-RRT計算樹中結點的能達集，當採樣點到結點的距離大於採樣點到該結點能達集的距離時, 該節點才有可能被選中進行擴展。

-  加入障礙物懲罰（RC-RRT、EG-RRT、ADD-RRT等）：降低靠近障礙物的結點獲得擴展的機率。

• 即時性改進

- anytime RRT先快速建構一個RRT,獲得一個可行解並記錄其代價.之後演算法會繼續取樣,但僅將有利於降低可行解代價的結點插入樹中,從而逐漸獲得較優的可行解.。

-  Replanning將整個規劃任務分解為若干等時間的子任務序列，在執行目前任務的同時規劃下一個任務。

• 最適性改進

- PRM*、RRG、RRT*：根據隨機幾何圖理論（在狀態空間中隨機取樣m個點,並將距離小於r(n)的點連起來,就構成了隨機幾何圖）對標準PRM 和RRT做出改進,得到了具有漸近最優性質的PRM*、RRG和RRT*演算法

3. 直接最佳化方法

在絕大多數情況下，不考慮高度的變化，自動駕駛的軌跡規劃問題是一個三維約束最佳化問題（2D空間時間T），因此，我們可以採用解耦的策略，將原始問題分解為幾個低維問題，從而大大降低求解難度。

1）Frenet座標系

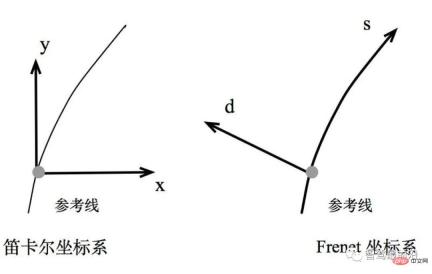
#圖7.Frenet座標系

#由於真實世界中的道路都是彎曲的，為了簡化求解最佳化問題的參數表達，在自動駕駛中通常會採用Frenet座標系。

在Frenet座標系中，我們使用道路的中心線作為參考線，使用參考線的切線向量t和法線向量n建立一個座標系，如右圖所示，它以車輛本身為原點，座標軸相互垂直，分為s方向（即沿著參考線的方向，通常被稱為縱向，Longitudinal）和d方向（或L方向，即參考線當前的法向，被稱為橫向，Lateral ），相較於笛卡爾座標系（左圖），Frenet座標係明顯地簡化了問題。

因為在公路行駛中，我們總是能夠簡單的找到道路的參考線（即道路的中心線），那麼基於參考線的位置的表示就可以簡單的使用縱向距離S（即沿著道路方向的距離）和橫向距離L（即偏離參考線的距離）來描述。

2）路徑-速度解耦法

在Frenet座標系中，路徑-速度解耦法分別優化路徑和速度，路徑優化主要考慮靜態障礙物，透過動態規劃產生一條靜態的參考路徑（SL維度），接著基於生成的路徑，考慮對速度的規劃（ST維度）。這一過程可以不斷迭代，從而實現對軌蹟的即時更新。在百度的開源自動駕駛平台Apollo中採用的EM planner就是基於類似的解決想法。此方案具有較強的靈活性，可普適性的適用於許多場景。

除此之外，也可以選擇不同的解耦方式，例如分別對縱向軌跡（ST維度）和橫向軌跡（LT維度）進行規劃。但需要指出的是，透過解耦的方法得到的解可能不是最優的，而且這種演算法不具備完備性，在一些複雜環境中可能找不到可行解。

4. 參數化曲線建構法

#圖8. 常見的參數化曲線建構法，引用自[19]

參數化曲線構造法的出發點是車輛本身的約束，包括運動學與動力學的約束，因此一般規劃的路徑需要是曲率連續的。這類方法根據起始點和目標點，考慮障礙物，透過建構一族符合車輛限制的曲線給出一條平滑路徑。

如圖8所示，常見的曲線有Dubins曲線（由直線和圓弧構成，是一種簡單車輛模型Dubin模型在二維空間中的最短曲線族），迴旋曲線，多項式曲線，貝塞爾曲線，樣條曲線等。單純應用參數化曲線構造法很難滿足實際複雜場景，因此現在越來越多的自動駕駛系統將其與其他方法結合，用來對已經規劃生成的軌跡做平滑處理，以滿足車輛運動學與動力學約束。

5. 人工位勢場法

#

人工位勢場法是受物理學中電磁場的啟發，假設障礙物和目標位置分別產生斥力和引力，從而可以沿著位場的最速梯度下降去規劃路徑。這類方法的一個關鍵問題是如何選擇合適的位勢場函數，例如：Stephen Waydo使用流函數進行平滑路徑的規劃[20]，Robert Daily在高速車輛上提出諧波場路徑規劃方法[21]。在簡單場景下，人工位勢場法具有較高的求解效率，但其存在的最大問題是可能陷入局部最小值，在這種情況下，所獲得的路徑不是最優，甚至可能找不到路徑。

05 演算法複雜度（Complexity）

在規劃問題中，對於演算法的評估除了考慮其時間和空間複雜度之外，還要考慮其是否具有完備性和最優性，退一步的情況下考慮其是否具有機率完備性和漸進性最優性。只要在了解這些性質的基礎上，我們才能針對不同的實際場景設計和應用不同的演算法，從而達到模型複雜和效率最優的最佳衡點。

1）完備性（Completeness）：如果在起始點和目標點間有路徑解存在，那麼一定可以得到解，如果得不到解那麼一定表示沒有解存在；

2）機率完備性（Probabilistically Completeness）：如果在起始點和目標點間有路徑解存在，只要規劃或搜尋的時間夠長，就一定能確保找到一條路徑解；

#3）最優性（Optimality）：規劃得到的路徑在某個評估指標上是最優的（評估指標一般為路徑的長度）

4）漸進最優性（Asymptotically optimality）：經過有限次規劃迭代後得到的路徑是接近最優的次優路徑，且每次迭代後都與最優路徑更加接近，是一個逐漸收斂的過程

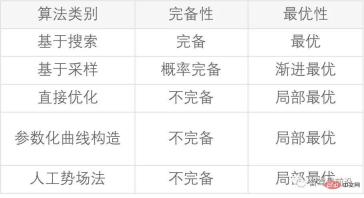
表1 常見演算法比較

06 未來發展趨勢

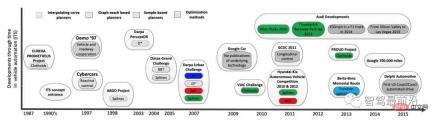
#圖9.自動駕駛發展時間軸及過程中重要的運動規劃演算法，引用自[19 ]

人類對自動駕駛的興趣最早可以追溯到1925年，近年來對自動駕駛的研究熱潮始於美國國防先進研究計畫局（Defense Advanced Research Projects Agency, DARPA ）在2004-2007年舉辦的3屆自動駕駛挑戰賽[22]，如圖9所示。在此之後，上文提到的各類決策規劃方法的有效性都被實際驗證。同時，將運動規劃方法與控制理論、狀態參數估計、機器學習等多領域方法結合的解決方案也不斷出現，成為未來的發展趨勢：

1）與車輛動力學結合：將動力學參數評估指標和最優規劃等結合，從最優控制角度進行規劃是近年來採用較多的方法，在這個過程中可以充分考慮車輛動力學因素，規劃出的軌跡更加合理。例如採用模型預測控制理論（Model Predictive Control）。其不足在於：對車輛的約束越多，優化其軌蹟的難度越大，較難實現線上的即時計算。

2）與狀態參數估計結合：狀態參數估計可以更準確地獲得車輛參數，因此可以將狀態估計器加入規劃模組中，透過線上估計車輛狀態並將其回饋給規劃器，提高軌跡品質.例如：不同地面類型會造成車輛滑移特性的變化，進而影響車輛狀態，透過結合估計參數即時重新規劃軌跡，閉環規劃進而提高軌跡安全性。

3）與機器學習結合：隨著以神經網路為代表的人工智慧的快速發展，許多傳統的規劃問題也帶來了新的解決思路。在自動駕駛領域，其發展趨勢包括：

• 端到端模型：使用一個深度神經網絡，直接根據車輛狀態和外部環境資訊得出車輛的控制訊號。儘管目前的端到端模型存在類似「黑箱」的不可解釋性，但相信隨著人類對深度神經網路理解的不斷加深，這一方法因其突出的簡潔高效優勢而具有很強的發展潛力。
• 決策與運動規劃模組融合
• 自動駕駛車輛在複雜環境中做出最優決策，這一問題與強化學習的定義非常吻合，因此如前文所述，隨著深度強化學習技術的快速發展，越來越多的研究團隊開始將其應用於自動駕駛決策規劃中，將行為決策與運動規劃模組融合，直接學習得到行車軌跡。為了解決環境獎勵函數不易獲得的問題，人們也提出了首先利用逆強化學習（IRL）根據人類專家演示學習，然後使用強化學習來學習最優策略。

以上是自動駕駛決策規劃技術詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章！