淺談Node.js如何實作蒙地卡羅樹搜索
- 青灯夜游轉載
- 2021-07-20 19:00:392241瀏覽
本篇文章給大家介紹一下使用Node.js如何實現蒙特卡羅樹搜索,並用蒙特卡洛樹搜索(MCTS)演算法來玩一個給定規則的遊戲,下面一起來看看吧!

本文假設讀者俱備一定的電腦科學知識,尤其是資料結構中關於樹結構的工作原理,還需要具備JavaScript (ES6 )的中級知識。推薦學習:《nodejs 教學》】
本文的目標很簡單:
實作蒙特卡羅樹搜尋(MCTS)演算法來玩一個給定規則的遊戲。
這整個過程將是指導性和實踐性的,並且忽略掉性能優化的部分。我將會對連結的程式碼片段進行簡要解釋,希望你能跟上我的腳步並花一些時間理解程式碼中複雜難懂的部分。
讓我們開始吧!
建立骨架檔案
在game.js 檔案中:
/** 代表游戏棋盘的类。 */
class Game {
/** 生成并返回游戏的初始状态。 */
start() {
// TODO
return state
}
/** 返回当前玩家在给定状态下的合法移动。 */
legalPlays(state) {
// TODO
return plays
}
/** 将给定的状态提前并返回。 */
nextState(state, move) {
// TODO
return newState
}
/** 返回游戏的胜利者。 */
winner(state) {
// TODO
return winner
}
}
module.exports = Game在monte-carlo.js 檔案中:
/** 表示蒙特卡洛树搜索的类。 */
class MonteCarlo {
/** 从给定的状态中,反复运行 MCTS 来建立统计数据。 */
runSearch(state, timeout) {
// TODO
}
/** 从现有的统计数据中获取最佳的移动。 */
bestPlay(state) {
// TODO
// return play
}
}
module.exports = MonteCarlo在index.js 檔案中:
const Game = require('./game.js')
const MonteCarlo = require('./monte-carlo.js')
let game = new Game()
let mcts = new MonteCarlo(game)
let state = game.start()
let winner = game.winner(state)
// 从初始状态开始轮流进行游戏,直到有玩家胜利为止
while (winner === null) {
mcts.runSearch(state, 1)
let play = mcts.bestPlay(state)
state = game.nextState(state, play)
winner = game.winner(state)
}
console.log(winner)先花點時間梳理一下程式碼吧。在腦海中搭建一個子版塊的鷹架,然後試著去明白這個東西。這是一個思維上的檢查點,先確保你明白它是如何組合在一起的,如果感到無法理解,就請留言吧,讓我看看我能為你做些什麼。
找到合適的遊戲
在開發一個MCTS 遊戲智能體的背景下,我們可以把我們真正的程式看作是實作MCTS 框架的程式碼,也就是monte-carlo.js 檔案中的程式碼。在 game.js 檔案中的遊戲專用程式碼是可以互換且即插即用的,它是我們使用 MCTS 框架的介面。我們主要是想做 MCTS 背後的大腦,它應該真的能在任何遊戲上運行。畢竟,我們感興趣的是一般性的遊戲玩法。
不過,為了測試我們的 MCTS 框架,我們需要選擇一個特定的遊戲,並使用該遊戲來運行我們的框架。我們希望看到 MCTS 框架在每個步驟中做出對我們選擇的遊戲有意義的決策。
做一個井字遊戲(Tic-Tac-Toe)怎麼樣呢?幾乎所有的遊戲入門教學都會用到它,它還有一些非常令我們滿意的特性:
- 大家之前都玩過。
- 它的規則很簡單,可以用演算法實作。
- 它有一份確定的完善的資訊。
- 它是一款對抗性的雙人遊戲。
- 狀態空間很簡單,可以在心理上進行建模。
- 狀態空間的複雜程度足以證明演算法的強大。
但是,井字遊戲真的很無聊,不是嗎?另外,你大概已經知道井字遊戲的最佳策略,這就失去了一些吸引力。有這麼多遊戲可以選擇,我們再選一個:四子棋(Connect Four#)怎麼樣?除了可能比井字遊戲享有更低的人氣外,它不僅有上面所列舉的特性,還可能讓玩家不那麼容易建立四子棋狀態空間的心理模型。

在我們的實作中,我們將使用Hasbro(孩之寶:美國著名玩具公司)的尺寸和規則,即6 行7 列,其中垂直、水平和對角線棋子數相連為4 就算勝利。棋子會從上方落下,並藉助重力落在自底向上數的第一個空槽。
不過在我們繼續講述之前,先說明一下。如果你有信心,你可以自己去實作任何你想要的遊戲,只要它遵守給定的遊戲 API。只是搞砸了,不能用的時候不要來抱怨。請記住,像國際象棋和圍棋這樣的遊戲太複雜了,即使是MCTS 也無法(有效地)獨自解決;谷歌在AlphaGo 中通過向MCTS 添加有效的機器學習策略來解決這個問題。如果你想玩自己的遊戲,你可以跳過接下來的兩個部分。
實作四子棋遊戲
現在,直接將game.js 改名為game-c4.js,將類別改名為Game_C4。同時,建立兩個新類別:State_C4 在state-c4.js 中表示遊戲狀態,Play_C4 在play-c4.js 中表示狀態轉換。
雖然這不是本文的主要內容,但是你自己會如何建構呢?
- 你会如何在
State_C4中表示一个游戏状态呢? - 在
Play_C4中,你将如何表示一个状态转换(例如一个动作)呢? - 你会如何把
State_C4、Play_C4和四子棋游戏规则 —— 用冰冷的代码放在Game_C4中吗?
注意,我们需要通过骨架文件 game-c4.js 中定义的高级 API 方法所要求的形式实现四子棋游戏。
你可以独立思考完成或者直接使用我完成的 play-c4.js、state-c4.js 和 game-c4.js 文件。
这是一个工作量很大的活,不是吗?至少对我来说是这样的。这段代码需要一些 JavaScript 知识,但应该还是很容易读懂的。最重要的工作在 Game_C4.winner() 中 —— 它用于在四个独立的棋盘中建立积分系统,而所有的棋盘都在 checkBoards 里面。每个棋盘都有一个可能的获胜方向(水平、垂直、左对角线或右对角线)。我们需要确保棋盘的三个面比实际棋盘大,方便为算法提供零填充。
我相信还有更好的方法。Game.winner() 的运行时性能并不是很好,具体来说,在大 O 表示法中,它是 O(rows * cols),所以性能并不是很好。通过在状态对象中存储 checkBoards,并且只更新 checkBoards 中最后改变状态的单元格(也会包含在状态对象中),可以大幅改善运行时性能,也许你以后可以尝试这个优化方法。
运行四子棋游戏
此时,我们将通过模拟 1000 次四子棋游戏来测试 Game_C4。点击获取 test-game-c4.js 文件。
在终端上运行 node test-game-c4.js。在一个相对现代的处理器和最新版本的 Node.js 上,运行 1000 次迭代应该会在一秒钟内完成:
$ node test-game-c4.js [ [ 0, 0, 0, 0, 0, 0, 2 ], [ 0, 2, 0, 0, 0, 0, 2 ], [ 0, 1, 0, 1, 2, 1, 2 ], [ 0, 2, 1, 2, 2, 1, 2 ], [ 0, 1, 1, 2, 1, 2, 1 ], [ 0, 1, 2, 1, 1, 2, 1 ] ] 0.549
二号棋手在内部用 -1 表示,这是为了方便 game-c4.js 的计算。用 2 代替 -1 的那段代码只是为了对齐棋盘输出结果。为了简便起见,程序只输出了一块棋盘,但它确实玩了另外的 999 次四子棋游戏。在单个棋盘输出之后,它应该输出一号棋手在所有 1000 盘棋中获胜的分数 —— 预计数值在 55% 左右,因为第一个棋手有先发优势。
分析现在的状况
我们已经实现一个带有 API 方法并且可以运行的游戏,这些 API 方法可以与 State 对象表示的游戏状态协同运行。我们现在的状况如何?
目标:实现蒙特卡洛树搜索(MCTS)算法来玩一个给定规则的游戏。
当然,我们还没有达到目的。刚才我们完成了一件非常重要的事情:让它设立一个切实的目标,并组成测试我们实现 MCTS 的核心模块。现在,我们进入正题。
实现蒙特卡洛树搜索
在这里,我将按照 MCTS 详解中类似的组织方式,我也会在一些地方用自己的话来阐明某些观点。
实现搜索树节点

为了存储从这些模拟中获得的统计信息,MCTS 从头开始建立了自己的搜索树。
现在请你回顾树结构知识。MCTS 是一个树结构搜索,因此我们需要使用树节点。我们将在 monte-carlo-node.js 的 MonteCarloNode 类中实现这些节点。然后,我们将在 MonteCarlo 中使用它来构建搜索树。
/** 代表搜索树中一个节点的类。 */
class MonteCarloNode {
constructor(parent, play, state, unexpandedPlays) {
this.play = play
this.state = state
// 蒙特卡洛的内容
this.n_plays = 0
this.n_wins = 0
// 树结构的内容
this.parent = parent
this.children = new Map()
for (let play of unexpandedPlays) {
this.children.set(play.hash(), { play: play, node: null })
}
}
...先再确认一下是否能够理解这些:
-
parent是MonteCarloNode父节点。 -
play是指从父节点到这个节点所做的Play。 -
state是指与该节点相关联的游戏State。 -
unexpandedPlays是Plays的一个合法数组,可以从这个节点进行。 -
this.children是由unexpandedPlays创建的,是Plays指向子节点MonteCarloNodes的一个 Map 对象(不完全是,见下文)。
MonteCarloNode.children 是一个从游戏哈希到对象的映射,包含游戏对象和相关的子节点。我们在这里包含了游戏对象,以便从它们的哈希中恢复游戏对象。
重要的是,Play 和 State 应该提供 hash() 方法。我们将在一些地方使用这些哈希作为 JavaScript 的 Map 对象,比如在 MonteCarloNode.children 中。
请注意,两个 State 对象应该被 State.hash() 认为是不同的 —— 即使它们有相同的棋盘状态 —— 如果每个对象通过不同的下棋顺序达到相同的棋盘状态。考虑到这一点,我们可以简单地让 State.hash() 返回一个字符串化的 Play 对象的有序数组,代表为达到该状态而下的棋。如果你获取了我的 state-c4.js,这个已经完成了。
现在我们将为 MonteCarloNode 添加成员方法。
...
/** 获取对应于给定游戏的 MonteCarloNode。 */
childNode(play) {
// TODO
// 返回 MonteCarloNode
}
/** 展开指定的 child play,并返回新的 child node。*/
expand(play, childState, unexpandedPlays) {
// TODO
// 返回 MonteCarloNode
}
/** 从这个节点 node 获取所有合法的 play。*/
allPlays() {
// TODO
// 返回 Play[]
}
/** 从这个节点 node 获取所有未展开的合法 play。 */
unexpandedPlays() {
// TODO
// 返回 Play[]
}
/** 该节点是否完全展开。 */
isFullyExpanded() {
// TODO
// 返回 bool
}
/** 该节点 node 在游戏树中是否为终端,
不包括因获胜而终止游戏。 */
isLeaf() {
// TODO
// 返回 bool
}
/** 获取该节点 node 的 UCB1 值。 */
getUCB1(biasParam) {
// TODO
// 返回 number
}
}
module.exports = MonteCarloNode方法可真多!
特别是,MonteCarloNode.expand() 将 MonteCarloNode.children 中未展开的空节点替换为实节点。这个方法将是四阶段的 MCTS 算法中阶段二:扩展的一部分,其他方法自行理解。
通常你可以自己实现这些,也可以获取完成的 monte-carlo-node.js。即使你自己做,我也建议在继续之前对照我完成的程序进行检查,以确保正常运行。
如果你刚获取到我完成的程序,请快速浏览一下源代码,就当是另一个心理检查点,重新梳理你的整体理解。这些都是简短的方法,你会在短时间内看懂它们。

尤其是 MonteCarloNode.getUCB1() 几乎是将上面的公式直接翻译成代码。这整个公式在上一篇文章中有详细的解释,再去看一下吧,这并不难理解,也是值得看的。
更新蒙特卡洛的类
目前的版本是 monte-carlo-v1.js,只是一个骨架文件。该类的第一个更新是增加 MonteCarloNode,并创建一个构造函数。
const MonteCarloNode = require('./monte-carlo-node.js')
/** 表示蒙特卡洛搜索树的类。 */
class MonteCarlo {
constructor(game, UCB1ExploreParam = 2) {
this.game = game
this.UCB1ExploreParam = UCB1ExploreParam
this.nodes = new Map() // map: State.hash() => MonteCarloNode
}
...MonteCarlo.nodes 允许我们获取任何给定状态的节点,这将是有用的。至于其他的成员变量,将它们与 MonteCarlo 联系起来就很有意义了。
...
/** 如果给定的状态不存在,就创建空节点。 */
makeNode(state) {
if (!this.nodes.has(state.hash())) {
let unexpandedPlays = this.game.legalPlays(state).slice()
let node = new MonteCarloNode(null, null, state, unexpandedPlays)
this.nodes.set(state.hash(), node)
}
}
...以上代码让我们可以创建根节点,还可以创建任意节点,这可能很有用。
...
/** 从给定的状态,反复运行 MCTS 来建立统计数据。 */
runSearch(state, timeout = 3) {
this.makeNode(state)
let end = Date.now() + timeout * 1000
while (Date.now() < end) {
let node = this.select(state)
let winner = this.game.winner(node.state)
if (node.isLeaf() === false && winner === null) {
node = this.expand(node)
winner = this.simulate(node)
}
this.backpropagate(node, winner)
}
}
...最后,我们来到了算法的核心部分。引用第一篇文章的内容,以下是过程描述:
在第 (1) 阶段,利用现有的信息反复选择连续的子节点,直至搜索树的末端。
接下来,在第 (2) 阶段,通过增加一个节点来扩展搜索树。
然后,在第 (3) 阶段,模拟运行到最后,决定胜负。
最后,在第 (4) 阶段,所选路径中的所有节点都会用模拟游戏中获得的新信息进行更新。
这四个阶段的算法反复运行,直至收集到足够的信息,产生一个好的移动结果。
...
/** 从现有的统计数据中获得最佳的移动。 */
bestPlay(state) {
// TODO
// 返回 play
}
/** 第一阶段:选择。选择直到不完全展开或叶节点。 */
select(state) {
// TODO
// 返回 node
}
/** 第二阶段:扩展。随机展开一个未展开的子节点。 */
expand(node) {
// TODO
// 返回 childNode
}
/** 第三阶段:模拟。游戏到终止状态,返回获胜者。 */
simulate(node) {
// TODO
// 返回 winner
}
/** 第四阶段:反向传播。更新之前的统计数据。 */
backpropagate(node, winner) {
// TODO
}
}接下来讲解四个阶段具体的实现方法,我们现在的版本是 monte-carlo-v2.js。
实现 MCTS 第一阶段:选择

从搜索树的根节点开始,我们通过反复选择一个合法移动,前进到相应的子节点来向下移动。如果一个节点中的一个、几个或全部合法移动在搜索树中没有对应的节点,我们就停止选择。
...
/** 第一阶段:选择。选择直到不完全展开或叶节点。 */
select(state) {
let node = this.nodes.get(state.hash())
while(node.isFullyExpanded() && !node.isLeaf()) {
let plays = node.allPlays()
let bestPlay
let bestUCB1 = -Infinity
for (let play of plays) {
let childUCB1 = node.childNode(play)
.getUCB1(this.UCB1ExploreParam)
if (childUCB1 > bestUCB1) {
bestPlay = play
bestUCB1 = childUCB1
}
}
node = node.childNode(bestPlay)
}
return node
}
...该函数通过查询每个子节点的 UCB1 值,使用现有的 UCB1 统计。选择 UCB1 值最高的子节点,然后对所选子节点的子节点重复这个过程,以此类推。
当循环终止时,保证所选节点至少有一个未展开的子节点,除非该节点是叶子节点。这种情况是由调用函数 MonteCarlo.runSearch() 处理的,所以我们在这里不必担心。
实现 MCTS 第二阶段:扩展

停止选择后,搜索树中至少会有一个未展开的移动。现在,我们随机选择其中的一个,然后我们创建该移动对应的子节点(图中加粗)。我们将这个节点作为子节点添加到选择阶段最后选择的节点上,扩展搜索树。节点中的统计信息初始化为
0次模拟中的0次胜利。
...
/** 第二阶段:扩展。随机展开一个未展开的子节点。 */
expand(node) {
let plays = node.unexpandedPlays()
let index = Math.floor(Math.random() * plays.length)
let play = plays[index]
let childState = this.game.nextState(node.state, play)
let childUnexpandedPlays = this.game.legalPlays(childState)
let childNode = node.expand(play, childState, childUnexpandedPlays)
this.nodes.set(childState.hash(), childNode)
return childNode
}
...再来看一下 MonteCarlo.runSearch()。扩展是在检查 if (node.isLeaf() === false && winner === null) 时完成的。很明显,如果在游戏树中没有可能的子节点 —— 例如,当棋盘满了的时候,是不可能进行扩展的。如果有赢家的话,我们也不想扩展 —— 这就像说当你的对手赢了的时候你应该停止玩游戏一样明显。
那么如果是叶子节点,会发生什么呢?我们只需用在该节点中获胜的人进行反向传播 —— 无论是玩家 1,玩家 -1,甚至是 0(平局)。同样,如果在任何节点上有一个非空的赢家,我们只需跳过扩展和模拟,并立即与该赢家(1 或 -1 或 0)进行反向传播。
反向传播 0 赢家是什么意思?用 MCTS 真的可以吗?真的可以用,后面再细讲。
实现 MCTS 第三阶段:模拟

从扩张阶段新建立的节点开始,随机选择棋步,反复推进对局状态。这样重复进行,直到对局结束,出现赢家。在此阶段不创建新节点。
...
/** 第三阶段:模拟。游戏到终止状态,返回获胜者。 */
simulate(node) {
let state = node.state
let winner = this.game.winner(state)
while (winner === null) {
let plays = this.game.legalPlays(state)
let play = plays[Math.floor(Math.random() * plays.length)]
state = this.game.nextState(state, play)
winner = this.game.winner(state)
}
return winner
}
...因为这里没有保存任何东西,所以这主要涉及到 Game,而 MonteCarloNode 的内容不多。
再看一下 MonteCarlo.runSearch(),模拟是在与扩展一样的检查 if (node.isLeaf() === false && winner === null) 时完成的。原因是:如果这两个条件之一成立,那么最后的赢家就是当前节点的赢家,我们只是用这个赢家进行反向传播。
实现 MCTS 第四阶段:反转
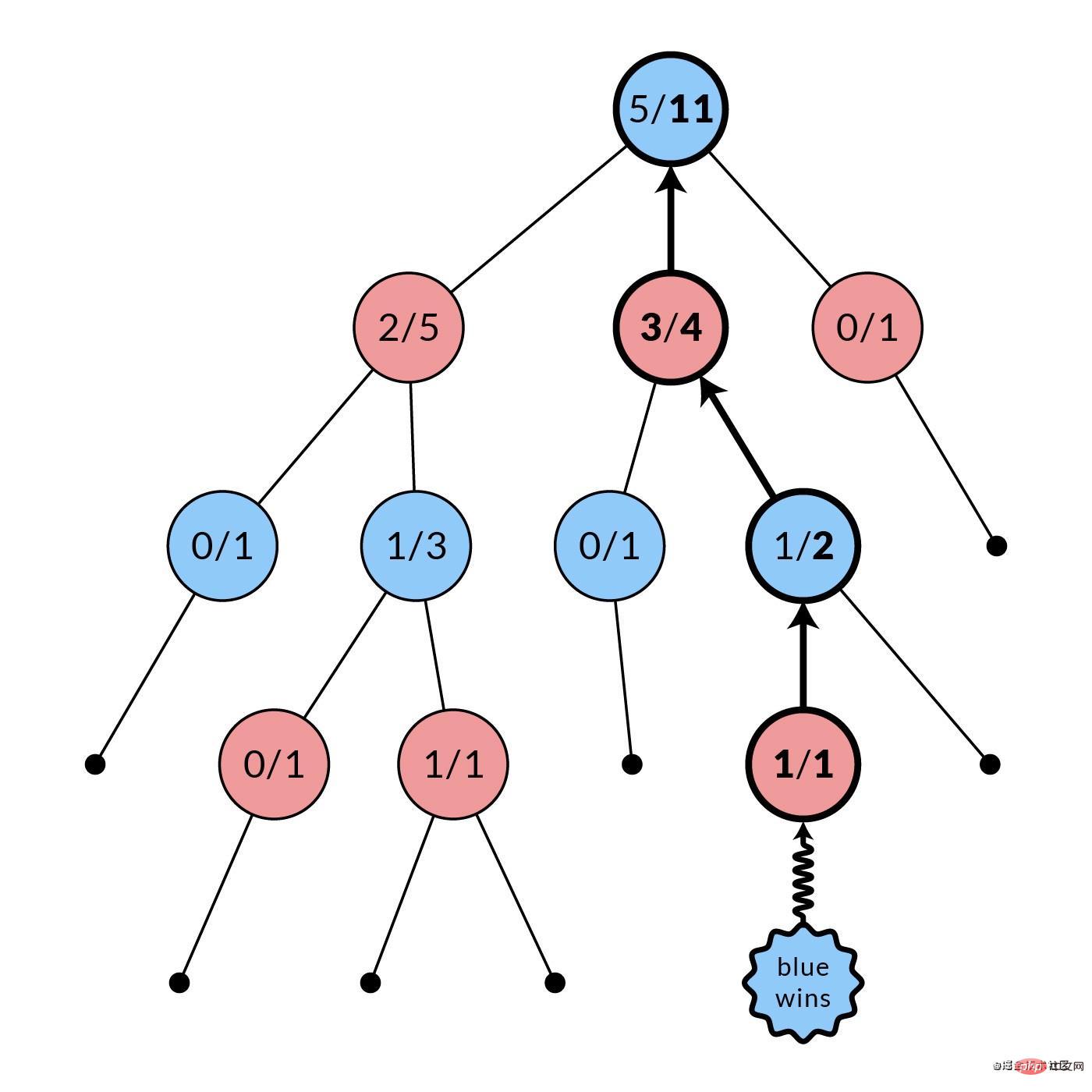
模拟阶段结束后,所有被访问的节点(图中粗体)的统计数据都会被更新。每个被访问的节点的模拟次数都会递增。根据哪个玩家获胜,其获胜次数也可能递增。在图中,蓝节点赢了,所以每个被访问的红节点的胜利数都会递增。这种反转是由于每个节点的统计数据是用于其父节点的选择,而不是它自己的。
...
/** 第四阶段:反向传播。更新之前的统计数据。 */
backpropagate(node, winner) {
while (node !== null) {
node.n_plays += 1
// 父节点的选择
if (node.state.isPlayer(-winner)) {
node.n_wins += 1
}
node = node.parent
}
}
}
module.exports = MonteCarlo这是影响下一次迭代搜索中选择阶段的部分。请注意,这假设是一个两人游戏,允许在 node.state.isPlayer(-winner) 中进行反转。你也许可以把这个函数泛化为 n 人游戏,做成 node.parent.state.isPlayer(winner) 之类的。
想一想,反向传播 0 赢家是什么意思?这相当于一盘平局,每个访问节点的 n_plays 统计数据都会增加,而玩家 1 和玩家 -1 的 n_wins 统计数据都不会增加。这种更新的行为就像两败俱伤的游戏,将选择推向其他游戏。最后,以平局结束的游戏和以失败结束的游戏一样,都有可能得不到充分的开发。这并没有破坏任何东西,但它导致了当平局比输棋更可取时的次优发挥。一个快速的解决方法是在平局时将双方的 n_wins 递增一半。
实现最佳游戏选择

MCTS(UCT) 的妙处在于,由于它的不对称性,树的选择和成长逐渐趋向于更好的移动。最后,你得到模拟次数最多的子节点,那就是你根据 MCTS 的最佳移动结果。
...
/** 从现有的统计数据中获得最佳的移动结果。 */
bestPlay(state) {
this.makeNode(state)
// 如果不是所有的子节点都被扩展,则信息不足
if (this.nodes.get(state.hash()).isFullyExpanded() === false)
throw new Error("Not enough information!")
let node = this.nodes.get(state.hash())
let allPlays = node.allPlays()
let bestPlay
let max = -Infinity
for (let play of allPlays) {
let childNode = node.childNode(play)
if (childNode.n_plays > max) {
bestPlay = play
max = childNode.n_plays
}
}
return bestPlay
}
...需要注意的是,选择最佳玩法有不同的策略。这里所采用的策略在文献中叫做 robust child,选择最高的 n_plays。另一种策略是 max child,选择最高的胜率 n_wins/n_plays。
实现统计自检和显示
现在,你应该可以在当前版本 index-v1.js 上运行 node index.js。但是,你不会看到很多东西。要想看到里面发生了什么,我们需要完成以下事情。
在 monte-carlo.js 文件中:
...
// 工具方法
/** 返回该节点和子节点的 MCTS 统计信息 */
getStats(state) {
let node = this.nodes.get(state.hash())
let stats = { n_plays: node.n_plays,
n_wins: node.n_wins,
children: [] }
for (let child of node.children.values()) {
if (child.node === null)
stats.children.push({ play: child.play,
n_plays: null,
n_wins: null})
else
stats.children.push({ play: child.play,
n_plays: child.node.n_plays,
n_wins: child.node.n_wins})
}
return stats
}
}
module.exports = MonteCarlo这让我们可以查询一个节点及其直接子节点的统计数据。做完这些,我们就完成了 MonteCarlo。你可以用你所拥有的东西来运行,也可以选择获取我完成的 monte-carlo.js。请注意,在我完成的版本中,bestPlay() 上有一个额外的参数来控制使用的最佳玩法策略。
现在,将 MonteCarlo.getStats() 整合到 index.js 中,或者获取我的完整版 index.js 文件。
接着运行 node index.js:
$ node index.js
player: 1
[ [ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ] ]
{ n_plays: 3996,
n_wins: 1664,
children:
[ { play: Play_C4 { row: 5, col: 0 }, n_plays: 191, n_wins: 85 },
{ play: Play_C4 { row: 5, col: 1 }, n_plays: 513, n_wins: 287 },
{ play: Play_C4 { row: 5, col: 2 }, n_plays: 563, n_wins: 320 },
{ play: Play_C4 { row: 5, col: 3 }, n_plays: 1705, n_wins: 1094 },
{ play: Play_C4 { row: 5, col: 4 }, n_plays: 494, n_wins: 275 },
{ play: Play_C4 { row: 5, col: 5 }, n_plays: 211, n_wins: 97 },
{ play: Play_C4 { row: 5, col: 6 }, n_plays: 319, n_wins: 163 } ] }
chosen play: Play_C4 { row: 5, col: 3 }
player: 2
[ [ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 1, 0, 0, 0 ] ]
{ n_plays: 6682,
n_wins: 4239,
children:
[ { play: Play_C4 { row: 5, col: 0 }, n_plays: 577, n_wins: 185 },
{ play: Play_C4 { row: 5, col: 1 }, n_plays: 799, n_wins: 277 },
{ play: Play_C4 { row: 5, col: 2 }, n_plays: 1303, n_wins: 495 },
{ play: Play_C4 { row: 4, col: 3 }, n_plays: 1508, n_wins: 584 },
{ play: Play_C4 { row: 5, col: 4 }, n_plays: 1110, n_wins: 410 },
{ play: Play_C4 { row: 5, col: 5 }, n_plays: 770, n_wins: 265 },
{ play: Play_C4 { row: 5, col: 6 }, n_plays: 614, n_wins: 200 } ] }
chosen play: Play_C4 { row: 4, col: 3 }
...
winner: 2
[ [ 0, 0, 2, 2, 2, 0, 0 ],
[ 1, 0, 2, 2, 1, 0, 1 ],
[ 2, 0, 2, 1, 1, 2, 2 ],
[ 1, 0, 1, 1, 2, 1, 1 ],
[ 2, 0, 2, 2, 1, 2, 1 ],
[ 1, 0, 2, 1, 1, 2, 1 ] ]完美!
总结
本文主要讲述如何使用 Node.js 实现蒙特卡洛树搜索,希望大家喜欢。下一篇文章将介绍如何优化,以及蒙特卡洛树搜索(MCTS)的现状。
感谢你的阅读!
英文原文地址:https://medium.com/@quasimik/implementing-monte-carlo-tree-search-in-node-js-5f07595104df
原文作者:Michael Liu
更多编程相关知识,请访问:编程入门!!
以上是淺談Node.js如何實作蒙地卡羅樹搜索的詳細內容。更多資訊請關注PHP中文網其他相關文章!

