資料結構時間複雜度

什麼是時間複雜度？

演算法中某個函數有n次基本運算重複執行，用T(n)表示，現在有某個輔助函數f(n),使得當n趨近於無窮大時，T （n)/f(n)的極限值為不等於零的常數，則稱f(n)為T(n)的同數量級函數，記作T(n)=O(f(n)),稱O (f(n)) 為演算法的漸進時間複雜度，簡稱時間複雜度。

通俗一點講，其實所謂的時間複雜度，就是找了一個同樣曲線類型的函數f(n)來表示這個演算法的在n不斷變大時的趨勢 。當輸入量n逐漸加大時，時間複雜度的極限情形稱為演算法的「漸近時間複雜度」。

計算時間複雜度的方法：

1、用常數1取代運行時間中的所有加法常數

2、修改後的運行次數函數中，只保留最高階項

3、移除最高階項的係數

依數量級遞增排列，常見的時間複雜度有：

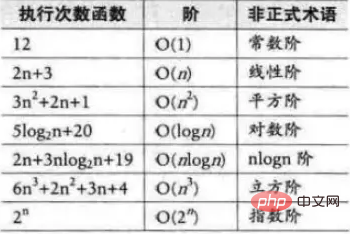
以上是資料結構時間複雜度的詳細內容。更多資訊請關注PHP中文網其他相關文章！