二分搜尋技術的時間複雜度
- (*-*)浩原創
- 2019-10-25 10:13:0113086瀏覽
二分搜尋法,它充分利用了元素間的次序關係,採用分治策略,可在最壞的情況下用O(log n)完成搜尋任務。
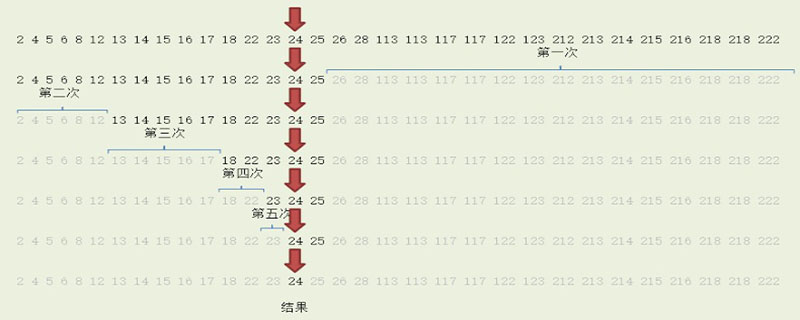
它的基本思想是,將n個元素分成個數大致相同的兩半,取a[n/2]與欲查找的x作比較,如果x=a[n/2]則找到x,演算法運算終止。 (推薦學習:web前端影片教學)
在電腦科學中,二分搜尋(英文:binary search),也稱為折半搜尋(英文:half-interval search) 、對數搜尋(英文:logarithmic search),是一種在有序數組中尋找某一特定元素的搜尋演算法。
搜尋過程從陣列的中間元素開始,如果中間元素剛好是要尋找的元素,則搜尋過程結束;如果某一特定元素大於或小於中間元素,則在陣列大於或小於中間元素的那一半中查找,而且跟開始一樣從中間元素開始比較。
如果在某一步驟陣列為空,則代表找不到。這種搜尋演算法每一次比較都使搜尋範圍縮小一半。
如果x
二分搜尋法的應用極為廣泛,而且它的思想易於理解,但是要寫一個正確的二分搜尋演算法也不是一件簡單的事。第一個二分搜尋演算法早在1946年就出現了,但是第一個完全正確的二分搜尋演算法直到1962年才出現。
Bentley在他的著作《Writing Correct Programs》中寫道,90%的電腦專家不能在2小時內寫出完全正確的二分搜尋演算法。
問題的關鍵在於準確地制定各次查找範圍的邊界以及終止條件的確定,正確地歸納奇偶數的各種情況,其實整理後可以發現它的具體演算法是很直觀的。
複雜度計算
時間複雜度:二分搜尋每次把搜尋區域砍掉一半,很明顯時間複雜度為O(log n)。 (n代表集合中元素的數量)
空間複雜度:O(1)。雖遞歸形式定義,但尾遞歸,可改寫為迴圈。
以上是二分搜尋技術的時間複雜度的詳細內容。更多資訊請關注PHP中文網其他相關文章!

