canvas實現高階貝塞爾曲線

本文主要介紹了canvas實現高階貝塞爾曲線(N階貝塞爾曲線生成器)，小編覺得挺不錯的，現在分享給大家，也給大家做個參考。一起跟著小編過來看看吧，希望能幫助大家。

寫在最前面

由於原生的Canvas最高只支援到三階貝塞爾曲線，那麼我想加入多個控制點怎麼辦呢？ （即便大部分複雜曲線都可以用3階貝塞爾來模擬）與此同時，關於貝塞爾控制點的位置我們很難非常直觀的清楚到底將控制點設置為多少可以形成我們想要的曲線。本著解決以上兩個痛點同時社群內好像並沒有N階的解決方案（js版）故這次作者非常認真的開源了bezierMaker.js！

bezierMaker.js理論上支援N階貝塞爾曲線的生成，同時提供了試驗場供開發者可以自行添加並拖曳控制點最終生成一組繪製動畫。非常直觀的讓開發者知道不同位置的控制點所對應的不同生成曲線。

如果你喜歡這件作品歡迎Star，畢竟star來之不易。 。

計畫地址：這裡✨✨✨

為什麼需要一個試驗場？

在繪製複雜的高階貝茲曲線時無法知道自己需要的曲線的控制點的精確位置。在試驗場中進行模擬，可以即時得到控制點的座標值，將得到的點座標變成物件陣列傳遞進BezierMaker類別就可以產生目標曲線

效果圖

# #  

功能

1. #[x] 試驗場可新增任意數量控制點

2. [x] 試驗場支援展示曲線繪製的形成動畫

3. [x] 控制點可自由拖曳

4. [x] 支援顯示貝塞爾曲線形成過程的切線

5. [x] 3階及以下貝塞爾曲線的繪圖採用原生API

引入

<script src="./bezierMaker.js"></script>

繪製##上面的效果圖為試驗場的使用，當你透過試驗場獲得控制點的準確座標之後，就可以呼叫bezierMaker.js進行曲線的直接繪製。

/**
 * canvas canvas的dom对象
 * bezierCtrlNodesArr 控制点数组，包含x，y坐标
 * color 曲线颜色
 */
var canvas = document.getElementById('canvas')
//3阶之前采用原生方法实现
var arr0 = [{x:70,y:25},{x:24,y:51}]
var arr1 = [{x:233,y:225},{x:170,y:279},{x:240,y:51}]
var arr2 = [{x:23,y:225},{x:70,y:79},{x:40,y:51},{x:300, y:44}]
var arr3 = [{x:333,y:15},{x:70,y:79},{x:40,y:551},{x:170,y:279},{x:17,y:239}]
var arr4 = [{x:53,y:85},{x:170,y:279},{x:240,y:551},{x:70,y:79},{x:40,y:551},{x:170,y:279}]
var bezier0 = new BezierMaker(canvas, arr0, 'black')
var bezier1 = new BezierMaker(canvas, arr1, 'red')
var bezier2 = new BezierMaker(canvas, arr2, 'blue')
var bezier3 = new BezierMaker(canvas, arr3, 'yellow')
var bezier4 = new BezierMaker(canvas, arr4, 'green')
bezier0.drawBezier()
bezier1.drawBezier()
bezier2.drawBezier()
bezier3.drawBezier()
bezier4.drawBezier()

繪製結果

#當控制點少於3個時，會適配使用原生的API接口。當控制點多於2個後，由我們自己實作的函數進行描點繪製。

核心原理

繪製貝塞爾曲線

繪製貝塞爾曲線的核心點在於貝塞爾公式的運用：

 

 
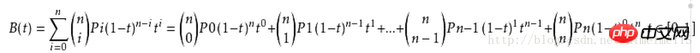
這個公式中的P0-Pn代表了從起點到各個控制點再到終點的各點與佔比t的各種冪運算。

BezierMaker.prototype.bezier = function(t) { //贝塞尔公式调用
    var x = 0,
        y = 0,
        bezierCtrlNodesArr = this.bezierCtrlNodesArr,
        //控制点数组
        n = bezierCtrlNodesArr.length - 1,
        self = this
    bezierCtrlNodesArr.forEach(function(item, index) {
        if(!index) {
            x += item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index) 
            y += item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index) 
        } else {
        //factorial为阶乘函数
            x += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index) 
            y += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index) 
        }
    })
    return {
        x: x,
        y: y
    }
}

對所有點進行遍歷同時根據目前佔比t的值(0<=t<=1)，計算出目前在貝塞爾曲線上的點座標x,y。 t的值作者分成了1000份，即每次運算t+=0.01。此時算出的x,y即所求的貝塞爾曲線分成了1000份之後的某一點。當t值從0~1遍歷1000次後產生1000個x,y對應座標，依序描點畫線即可模擬出高階貝塞爾曲線。

對於貝塞爾公式的推導作者會在之後的文章中專門說明，現在你只需要知道我們透過貝塞爾公式計算出實際貝塞爾曲線被等分成了1000份的各點，用直線連接各點後即可模擬出類曲線。

對於模擬場貝塞爾曲線產生動畫的實作

這個部分相關程式碼可以參考這裡

整體思路是用遞歸的方式來將每個一層控制點當做1階貝塞爾函數來計算下一層控制點並對應連線。具體邏輯作者會留到深入講解貝塞爾曲線公式原理的時候一起梳理一下試驗場的動畫生成原理~

#相關推薦：

使用CSS做貝塞爾曲線

貝塞爾曲線的應用詳解

#實作canvas貝塞爾曲線效果程式碼示範

################################################################

以上是canvas實現高階貝塞爾曲線的詳細內容。更多資訊請關注PHP中文網其他相關文章！