總結有關python實作八大排序演算法(上)
- 巴扎黑原創
- 2017-09-16 10:15:372466瀏覽
這篇文章主要為大家詳細介紹了python實作八大排序演算法的第一篇,具有一定的參考價值,有興趣的夥伴們可以參考一下
##排序
#排序是計算機內經常進行的一種操作,其目的是將一組”無序”的記錄序列調整為”有序”的記錄序列。分內部排序和外部排序。若整個排序過程不需要存取外存便能完成,則稱此類排序問題為內部排序。反之,若參加排序的記錄數量很大,整個序列的排序過程不可能完全在記憶體中完成,需要存取外存,則稱此類排序問題為外部排序。內部排序的過程是一個逐步擴大記錄的有序序列長度的過程。 看圖使理解更清晰深刻: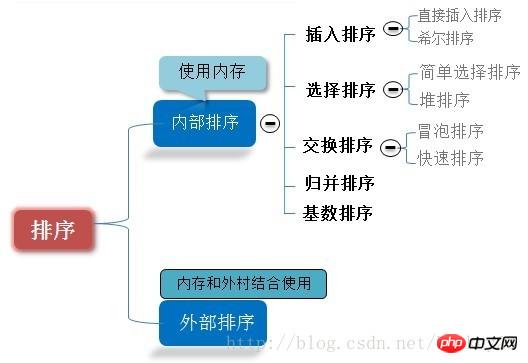
常見排序演算法
快速排序、希爾排序、堆排序、直接選擇排序不是穩定的排序演算法,而基數排序、冒泡排序、直接插入排序、折半插入排序、歸併排序是穩定的排序演算法本文將用Python實作冒泡排序、插入排序、希爾排序、快速排序、直接選擇排序、堆排序、歸併排序、基數排序這八大排序演算法。1. 冒泡排序(Bubble Sort)
演算法原理:已知一組無序資料a[1]、a[ 2]、……a[n],需將其依升序排列。先比較a[1]與a[2]的值,若a[1]大於a[2]則交換兩者的值,否則不變。再比較a[2]與a[3]的值,若a[2]大於a[3]則交換兩者的值,否則不變。再比較a[3]與a[4],以此類推,最後比較a[n-1]與a[n]的值。這樣處理一輪後,a[n]的數值一定是這組數據中最大的。再對a[1]~a[n-1]以相同方法處理一輪,則a[n-1]的值一定是a[1]~a[n-1]中最大的。再對a[1]~a[n-2]以相同方法處理一輪,以此類推。共處理n-1輪後a[1]、a[2]、……a[n]就以升序排列了。降序排列與升序排列相類似,若a[1]小於a[2]則交換兩者的值,否則不變,後面以此類推。 總的來講,每一輪排序後最大(或最小)的數將移動到資料序列的最後,理論上總共要進行n(n-1)/2次交換。缺點:慢,每次只能移動相鄰兩個資料。
#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst1 = [2,5435,67,445,34,4,34]
def bubble_sort_basic(lst1):
lstlen = len(lst1);i = 0
while i < lstlen:
for j in range(1,lstlen):
if lst1[j-1] > lst1[j]:
#对比相邻两个元素的大小,小的元素上浮
lst1[j],lst1[j-1] = lst1[j-1],lst1[j]
i += 1
print 'sorted{}: {}'.format(i, lst1)
print '-------------------------------'
return lst1
bubble_sort_basic(lst1)
#冒泡排序演算法的改進
對於全員無序或沒有重複元素的序列,上述演算法在同一思路上是沒有改進餘地的,但是如果一個序列中存在重複元素或者部分元素是有序的呢,這種情況下必然會存在不必要的重複排序,那麼我們可以在排序過程中加入一標誌性變數change,用於標誌某一趟排序過程中是否有資料交換,如果進行某一趟排序時並沒有進行資料交換,則表示資料已經按要求排列好,可立即結束排序,避免不必要的比較過程,改進後示例代碼如下:lst2 = [2,5435,67,445,34,4,34]
def bubble_sort_improve(lst2):
lstlen = len(lst2)
i = 1;times = 0
while i > 0:
times += 1
change = 0
for j in range(1,lstlen):
if lst2[j-1] > lst2[j]:
#使用标记记录本轮排序中是否有数据交换
change = j
lst2[j],lst2[j-1] = lst2[j-1],lst2[j]
print 'sorted{}: {}'.format(times,lst2)
#将数据交换标记作为循环条件,决定是否继续进行排序
i = change
return lst2
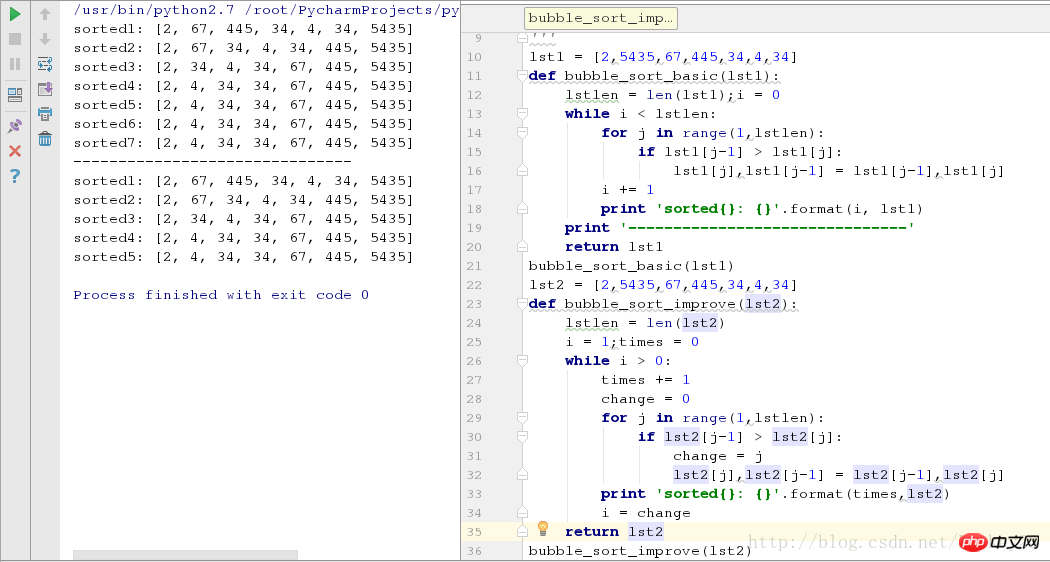
bubble_sort_improve(lst2)兩種情況下運行截圖如下:
2.選擇排序(Selection Sort)
演算法原理:每一趟從待排序的資料元素中選出最小(或最大)的一個元素,順序放在已排好序的數列的最後,直到全部待排序的資料元素排完。n個記錄的檔案的直接選擇排序可經過n-1趟直接選擇排序得到有序結果:
②第1趟排序
在無序區R[1..n]中選出關鍵字最小的記錄R[k],將它與無序區的第1個記錄R[1]交換,使R[1..1]和R[2..n]分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區。
……
③第i趟排序
第i趟排序開始時,目前有序區和無序區分別為R[1..i-1]和R(1≤i≤n -1)。此行程排序從目前無序區選出關鍵字最小的記錄R[k],將它與無序區的第1個記錄R交換,使R[1..i]和R分別變成記錄個數增加1個的新有序區和記錄個數減少1個的新無序區。
這樣,n個記錄的檔案的直接選擇排序可經過n-1趟直接選擇排序得到有序結果。
优点:移动数据的次数已知(n-1次);
缺点:比较次数多,不稳定。
python代码实现:
# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment:win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def selection_sort(lst):
lstlen = len(lst)
for i in range(0,lstlen):
min = i
for j in range(i+1,lstlen):
#从 i+1开始循环遍历寻找最小的索引
if lst[min] > lst[j]:
min = j
lst[min],lst[i] = lst[i],lst[min]
#一层遍历结束后将最小值赋给外层索引i所指的位置,将i的值赋给最小值索引
print('The {} sorted: {}'.format(i+1,lst))
return lst
sorted = selection_sort(lst)
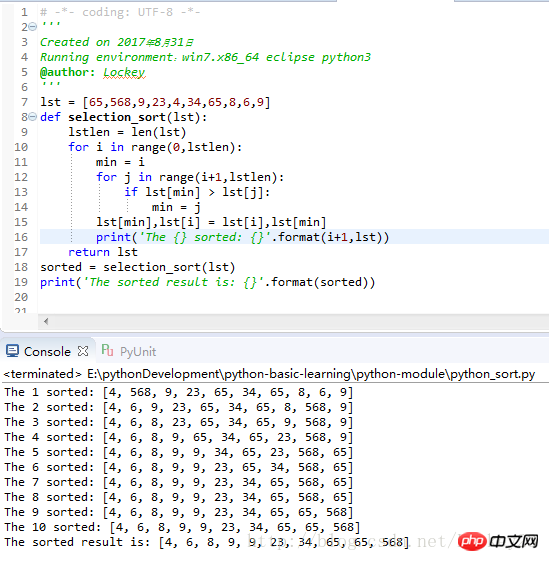
print('The sorted result is: {}'.format(sorted))运行结果截图:
3. 插入排序
算法原理:
已知一组升序排列数据a[1]、a[2]、……a[n],一组无序数据b[1]、b[2]、……b[m],需将二者合并成一个升序数列。首先比较b[1]与a[1]的值,若b[1]大于a[1],则跳过,比较b[1]与a[2]的值,若b[1]仍然大于a[2],则继续跳过,直到b[1]小于a数组中某一数据a[x],则将a[x]~a[n]分别向后移动一位,将b[1]插入到原来a[x]的位置这就完成了b[1]的插入。b[2]~b[m]用相同方法插入。(若无数组a,可将b[1]当作n=1的数组a)
优点:稳定,快;
缺点:比较次数不一定,比较次数越多,插入点后的数据移动越多,特别是当数据总量庞大的时候,但用链表可以解决这个问题。
算法复杂度
如果目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1)次。平均来说插入排序算法的时间复杂度为O(n^2)。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。
python代码实现:
# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment:win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def insert_sort(lst):
count = len(lst)
for i in range(1, count):
key = lst[i]
j = i - 1
while j >= 0:
if lst[j] > key:
lst[j + 1] = lst[j]
lst[j] = key
j -= 1
print('The {} sorted: {}'.format(i,lst))
return lst
sorted = insert_sort(lst)
print('The sorted result is: {}'.format(sorted))运行结果截图:
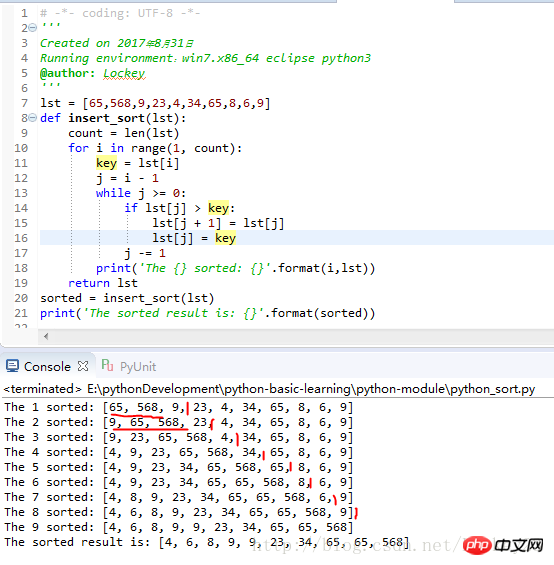
由排序过程可知,每次往已经排好序的序列中插入一个元素,然后排序,下次再插入一个元素排序。。。直到所有元素都插入,排序结束
4. 希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。
算法原理
算法核心为分组(按步长)、组内插入排序
已知一组无序数据a[1]、a[2]、……a[n],需将其按升序排列。发现当n不大时,插入排序的效果很好。首先取一增量d(d
python代码实现:
#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def shell_sort(lists):
print 'orginal list is {}'.format(lst)
count = len(lists)
step = 2
times = 0
group = int(count/step)
while group > 0:
for i in range(0, group):
times += 1
j = i + group
while j < count:
k = j - group
key = lists[j]
while k >= 0:
if lists[k] > key:
lists[k + group] = lists[k]
lists[k] = key
k -= group
j += group
print 'The {} sorted: {}'.format(times,lists)
group = int(group/step)
print 'The final result is: {}'.format(lists)
return lists
shell_sort(lst)运行测试结果截图: 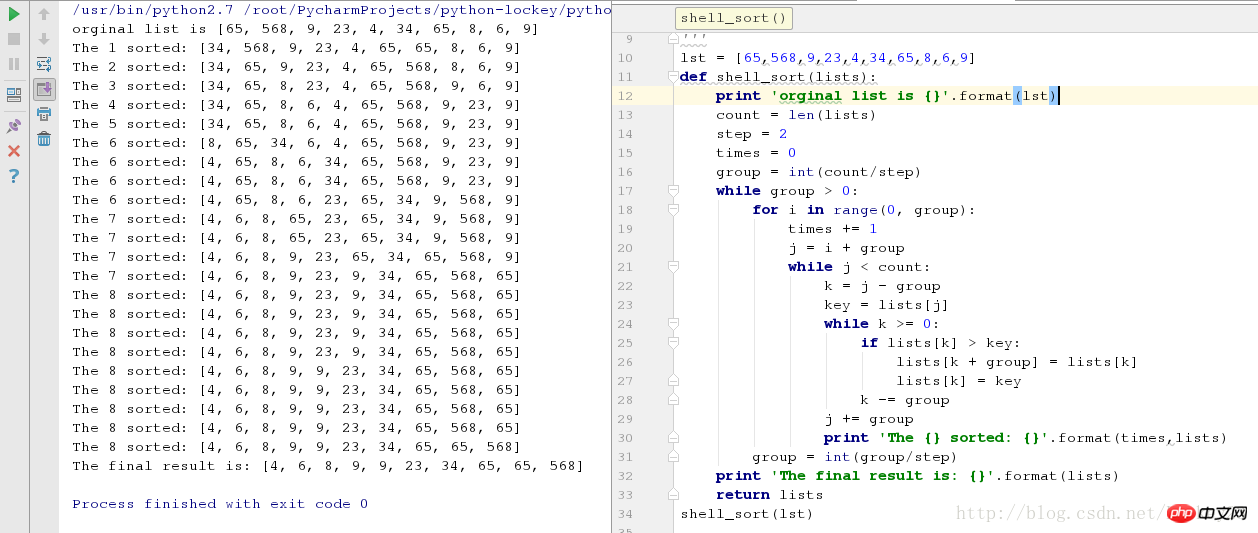
过程分析:
第一步:
1-5:将序列分成了5组(group = int(count/step)),如下图,一列为一组:

然后各组内进行插入排序,经过5(5组*1次)次组内插入排序得到了序列:
The 1-5 sorted:[34, 65, 8, 6, 4, 65, 568, 9, 23, 9]

第二步:
6666-7777:将序列分成了2组(group = int(group/step)),如下图,一列为一组:
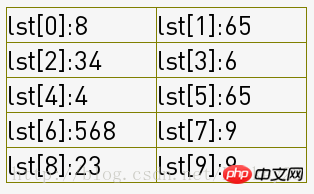
然后各组内进行插入排序,经过8(2组*4次)次组内插入排序得到了序列:
The 6-7 sorted: [4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

第三步:
888888888:对上一个排序结果得到的完整序列进行插入排序:
[4, 6, 8, 9, 23, 9, 34, 65, 568, 65]
经过9(1组*10 -1)次插入排序后:
The final result is: [4, 6, 8, 9, 9, 23, 34, 65, 65, 568]
希爾排序時效分析很難,關鍵碼的比較次數與記錄移動次數依賴於增量因子序列的選取,特定情況下可以準確估算出關鍵碼的比較次數和記錄的移動次數。目前還沒有人給出選取最好的增量因子序列的方法。增量因子序列可以有各種取法,有取奇數的,也有取質數的,但需要注意:增量因子中除1 外沒有公因子,且最後一個增量因子必須為1。希爾排序方法是一個不穩定的排序方法
以上是總結有關python實作八大排序演算法(上)的詳細內容。更多資訊請關注PHP中文網其他相關文章!

