pooling的原理與Python實現

本文首先闡述pooling所對應的操作，然後分析pooling背後蘊含的一些道理，最後給出pooling的Python實現。

一、pooling所對應的操作

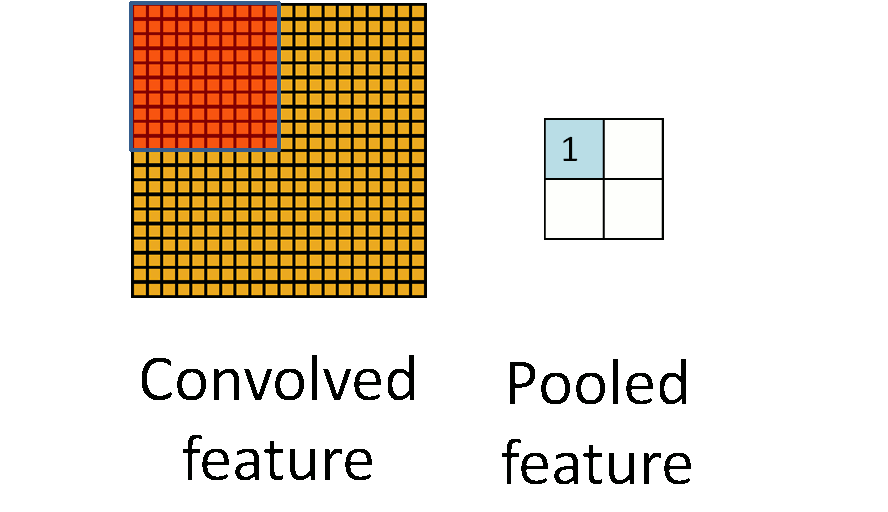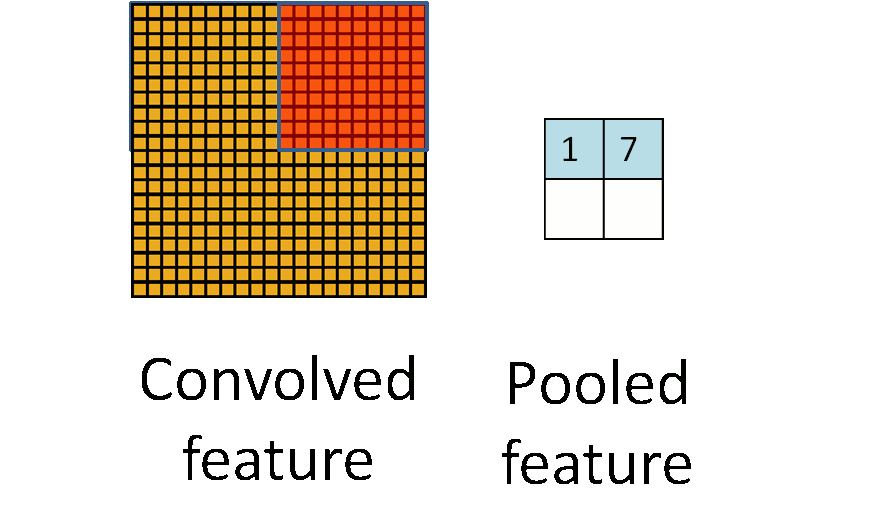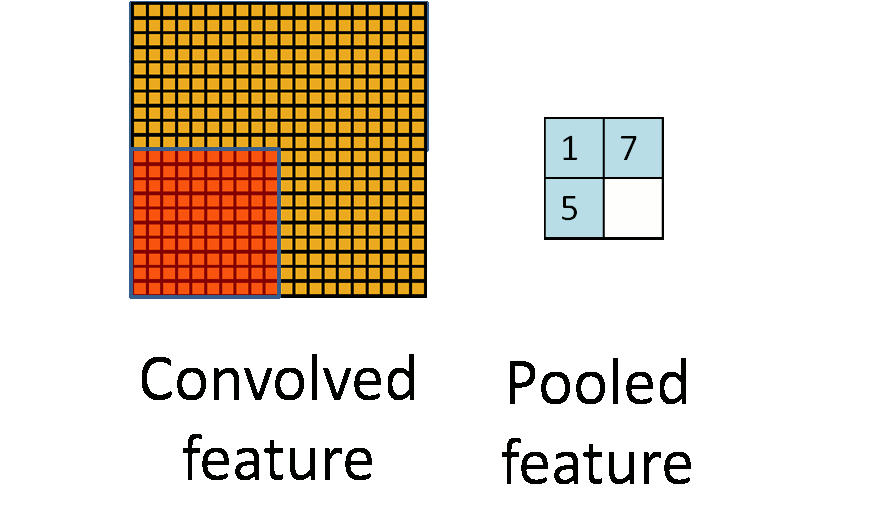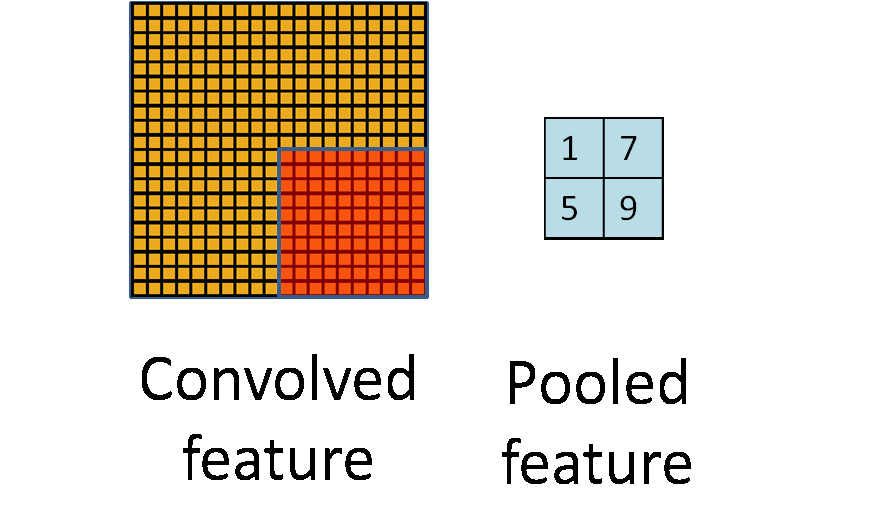
首先從整體上對pooling有一個直觀的概念（也就是對pooling的輸入、輸出以及具體功能進行描述，但是忽略具體的實現細節）：pooling的輸入是一個矩陣，輸出是一個矩陣；完成的功能是，對輸入矩陣的一個局部區域進行運作，使得該區域對應的輸出能夠最佳的代表該區域的特性。如圖1所示，左圖黃色矩陣代表輸入矩陣，右圖藍色矩陣代表輸出矩陣；動態的橘色矩陣代表選定輸入矩陣的一個局部區域，然後找出該區域的一個最佳代表出來，最後將所有選出的代表依照與原始輸入矩陣對應的空間位置關係在輸出矩陣中進行排序。

這一過程可以用選舉過程來類比。假如要選北京市長，可行的做法是，北京的每個區各選一個最符合該區權益的代表，然後由選出的代表們決定如何選取北京市長。當然了，我們希望每一個區選出的代表最能符合該區的權益。與pooling做一個簡單類比，北京〈-〉輸入矩陣；朝陽區、海淀區等〈-〉局部區域；各區代表〈-〉輸出矩陣（如果他們開會的時候按照地理位置就坐，這就和pooling的特性很像了）。

二、pooling背後蘊含的道理

在局部區域選取代表的過程中，我們一般的做法是：選取該區域最有聲望的人作為代表（對應max pooling）或選取最能代表該區域所有人一般特性的人作為代表（對應mean pooling），於此對應的是，pooling中也存在兩種常用的做法：局部區域值最大的勝出作為該區域的代表或將該區域所有的值取平均作為該區域的代表。

 

選取該區域最有聲望的人作為代表 vs 選取最能代表該區域所有人一般特性的人作為代表 好處是：

1） 局部區域最有聲望的人在選市長時不宜出現偏差，但他有可能倚老賣老，不能代表該區域一般民眾的看法（局部的最大值，容易忽略該區域的一般特性）

2） 最能代表該區域所有人一般特性的人雖然能夠代表該區域所有居民的最大權益，但由於他的認知能力有限（局部平均值較小，所以說他認知能力有限），在選市長時容易出現偏差。

3） 如果該區域內的人存在一定程度的自由活動的話（對應的是平移、旋轉不變性），對上述兩種選代表的方式基本上是沒有影響的。

 

pooling的正規解釋

依據相關理論：（1）鄰近大小受限造成的估計值變異數增大；（2）誤差造成估計平均值的偏移。一般來說，mean-pooling能減少第一種誤差，更多的保留圖像的背景信息，max-pooling能減小第二種誤差，更多的保留紋理資訊。

 

一般情況下pooling的輸入維度高、輸出維度低，這在一定程度上可以理解為降維，根據上述對pooling原理的闡述，我們可以推斷，這種降維過程極大的保留了輸入的一些最重要的資訊。在實際應用pooling的過程中，我們需要根據實際問題的特點，具體分析了。其實，知道了pooling的操作及其原理，如果她與具體問題結合的較好，則不失為一個很好的創新點哦，哈哈。

 

三、pooing的Python實作

筆者在寫程式碼時的一些思考如下，核心就是將一個複雜問題分割為一個可以直接用程式碼實現的問題：

1） 輸入矩陣可以是mxn，也可以為mxnxp，如果直接考慮這兩種形式寫程式碼的時候無從下手（要考慮的情況有點多，而且多維的矩陣我自己容易搞暈）。仔細分析發現如果我將        mxn矩陣的pooling實現，那麼mxnxp矩陣就可以運用mxn矩陣的實現輕而易舉實現了。

2） 針對mxn矩陣輸入，有可能圖1橘色方框不能剛好覆蓋輸入矩陣，因此需要對輸入矩陣進行擴展。擴充也很簡單，只要最後一個poolStride對應的poolSize能夠涵蓋輸入矩陣，      其他的肯定就可以涵蓋了。

3） 最後就是for循環進行類似操作過程處理了。

def pooling(inputMap,poolSize=3,poolStride=2,mode='max'):
    """INPUTS:
              inputMap - input array of the pooling layer
              poolSize - X-size(equivalent to Y-size) of receptive field
              poolStride - the stride size between successive pooling squares
       
       OUTPUTS:
               outputMap - output array of the pooling layer
               
       Padding mode - 'edge'
    """
    # inputMap sizes
    in_row,in_col = np.shape(inputMap)
    
    # outputMap sizes
    out_row,out_col = int(np.floor(in_row/poolStride)),int(np.floor(in_col/poolStride))
    row_remainder,col_remainder = np.mod(in_row,poolStride),np.mod(in_col,poolStride)
    if row_remainder != 0:
        out_row +=1
    if col_remainder != 0:
        out_col +=1
    outputMap = np.zeros((out_row,out_col))
    
    # padding
    temp_map = np.lib.pad(inputMap, ((0,poolSize-row_remainder),(0,poolSize-col_remainder)), 'edge')
    
    # max pooling
    for r_idx in range(0,out_row):
        for c_idx in range(0,out_col):
            startX = c_idx * poolStride
            startY = r_idx * poolStride
            poolField = temp_map[startY:startY + poolSize, startX:startX + poolSize]
            poolOut = np.max(poolField)
            outputMap[r_idx,c_idx] = poolOut
    
    # retrun outputMap
    return  outputMap
# 测试实例
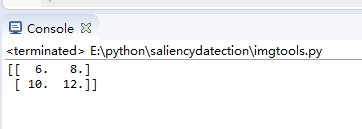
test = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
test_result = pooling(test, 2, 2, 'max')
print(test_result)

測試結果：

總結： 先理解一項技術的輸入、輸出以及其完成的功能；然後在生活中尋找類似的例子；最後，將該技術分解為可以實現的步驟。